A ball of mass m is attached to a fixed point by a light inextensible string describe a circle in a verticle plane. The tension in the string has the values αmg and βmg, respectively, when the particle is at the highest and the lowest point in the path. find the relation between α and β.
v2=u2−2g×2L=u2−4gL
At the lowest point:
T1−mg=μ2L
T1−mg=μ2L
βmg=mg+μ2L⇒μ2L=(β−1)mg
T2+mg=mv2L
αmg+mg=mL(u2−4gL)
(α+1)mg=μ2L−4mg
(α+1)mg=mu2L−4mg
=(β−1)mg−4mg
α+1=β−1−4
α+1=β−5⇒β=α+6
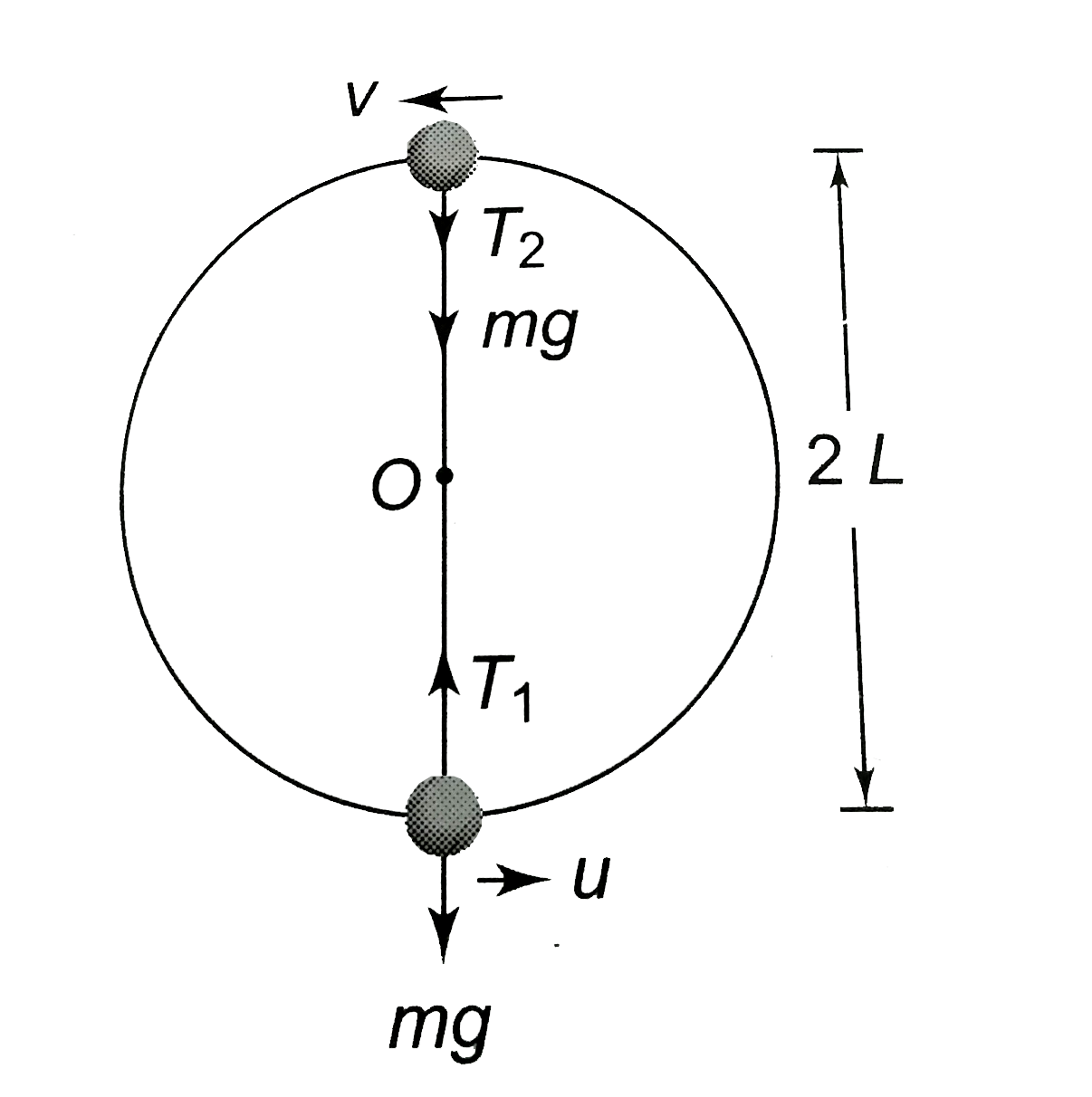
Topper's Solved these Questions
Similar Questions
A small body of mass m is tried to a string and revolved in a vertical circle of radius r. If the tension in the string at the highest point is mg, what is its speed there?
View SolutionA stone of mass m tied to a light inextensible sting of length L(=103m) is whirling in a circular path of radius L in a verticle plane. If the ratio of the maximum to the minimum tension is four, find the speed of the stone at the highest point of the circle.
View Solution
Knowledge Check
A heavy particle of weight w, attached to a fixed point by a light inextensible string describes a circle in a vertical plane. The tension in the string has the values nw and mw respectively when the particle is at the highest and lowest points in the path. Then :
Am+n=6Bmn=2Cm−n=−6Dn−m=−6A stone of mass m is tied to a string and is moved in a vertical circle of radius r making n revolution per minute. The total tension in the string when the stone is its lowest point is.
Am[g+4π2r]Bm[g+π2n2r260]Cm[g+π2n2r900]Dm[g+n2r2]A particle is projected so as to just move along a vertical circle of radius r. The ratio of the tension in the string when the particle is at the lowest and highest point on the circle is -
A1Bfinite but largeCzeroDInfinite
A particle tied to a string describes a vertical circular motion of radius r continually. If it has a velocity √3gr at the highest point, then the ratio of the respective tensions in the string holding it at the highest and lowest points is
View SolutionA small ball of mass m is attached to a string of lengh R and moves in a vertical circle with a speed v m/s about a fixed point O as illustrated in fig. Find the tension in the string, when it makes an angle θ with the vertical, in terms of v,θ and g.
View SolutionA particle of mass m is attached to one end of a light inextensible string and the other end of the string is fixed in vertical plane as shown. Particle is given a horizontal velocity u=√52gl
The tension in the string at an instant when acceleration of the particle is horizontal and √3g is
View SolutionA stone of mass 1 kg tied to a light inextensible string of lenth L=103m, whirling in a circular path in a vertical plane. The ratio of maximum tension to the minimum tension in the string is 4. If g is taken to be 10ms−2, the speed of the stone at the highest point of the circle is
View SolutionA ball of mass m is attached to a string whose other end is fixed. The system is free to rotate in vertical plane. When the ball swings, no work is done on the ball by the tension in the string. Which of the following statement is the correct explanation?
View Solution
