A ball of mass m moving horizotally which velocity u hits a wedge of mass M. The wedge is situated on a smooth horizontal source. If after striking with wedge the ball starts moving in vertical direction and the wedge starts moving in horizotal plane. calculate
a. the velocity of wedge V.
b. the velocity (v) at which the ball moves in vertical direction.
c. the impulse imparted by the ball on the wedge.
d. the coefficient of restitution e=?
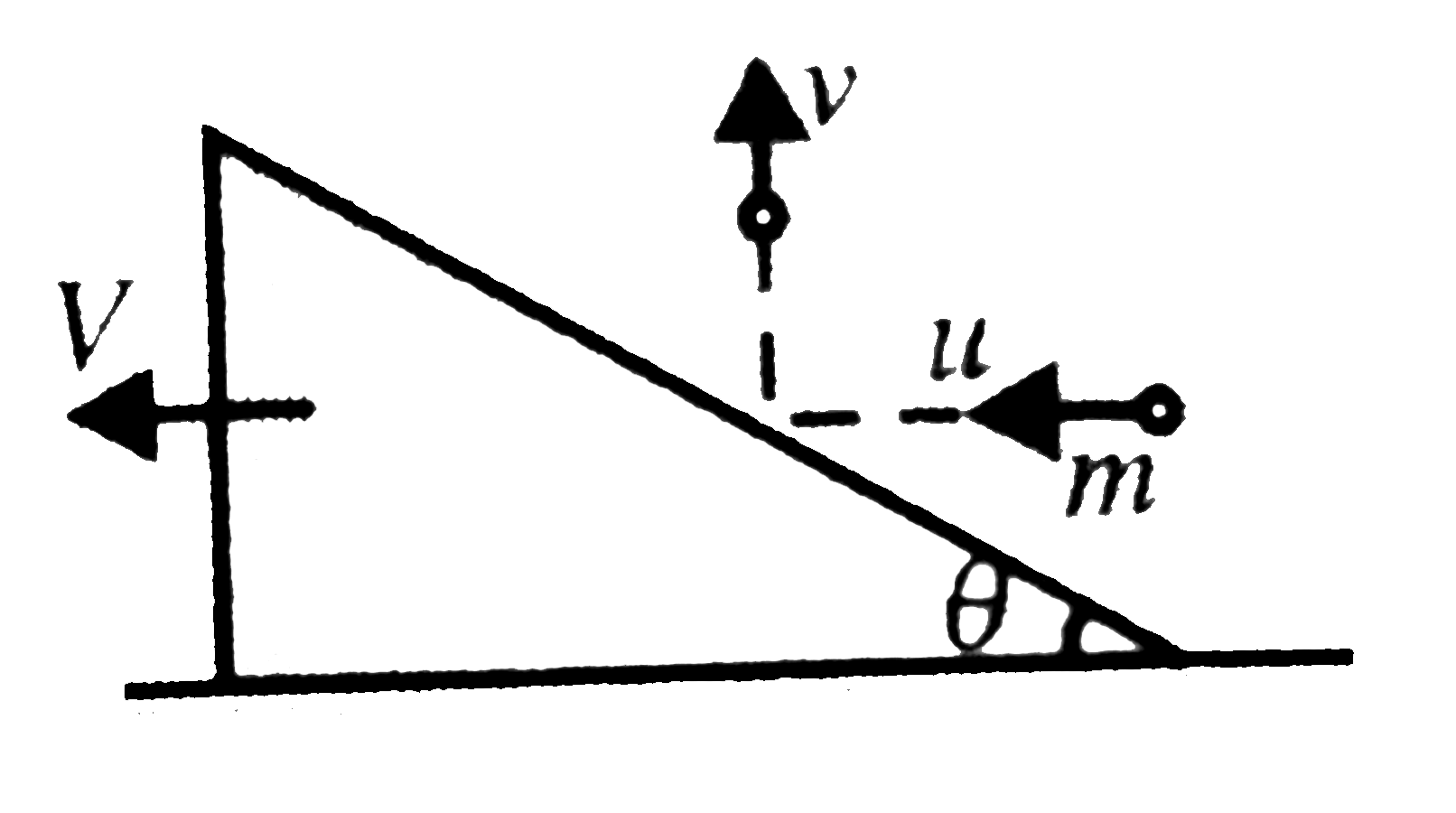
a. As no external force is acting on the system in horizontal direction the linear momentum should be constant and conserved in horizontal direction.
Let velocity of wedge after collision be V.
Then mu=MV⇒V=muM………..i
b. As there is no impulse on the ball in the direction parallel to sloping side hence the veloicty of ball along the slope (tangent direction) should remain unchanged,
⇒ucosθ=vsinθ ..........ii
c. we can find the values of v and V by impulse approach, when ball hits the wedge the impulse is generated between ball and wedge in the direction perpendicular to slopping surface. (normal direction).

For ball: mu−Jsinθ=0
Jsinθ=mu
Jcosθs=mv
from eqn i and ii v=ucotθ
From eqn iii J=mucosecθ,
Jsinθ=mV⇒V=JsinθM
Which gives V=μM
d. The direction of restitution is given as

(v2−v1)n−e(u1−u2)n
[Vsinθ−(−vcosθ)]=e[usinθ−0]
e=Vsinθ+vcosθusinθ
e=Vu+vucotθ=muM+(cotθ)cothη
e=mM+cot2θ
Topper's Solved these Questions
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Solved Examples
13 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Exercise 1.1
20 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICSCHAPTER - CALORIMETRYEXERCISE - Solved Example
13 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICSCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
Similar Questions
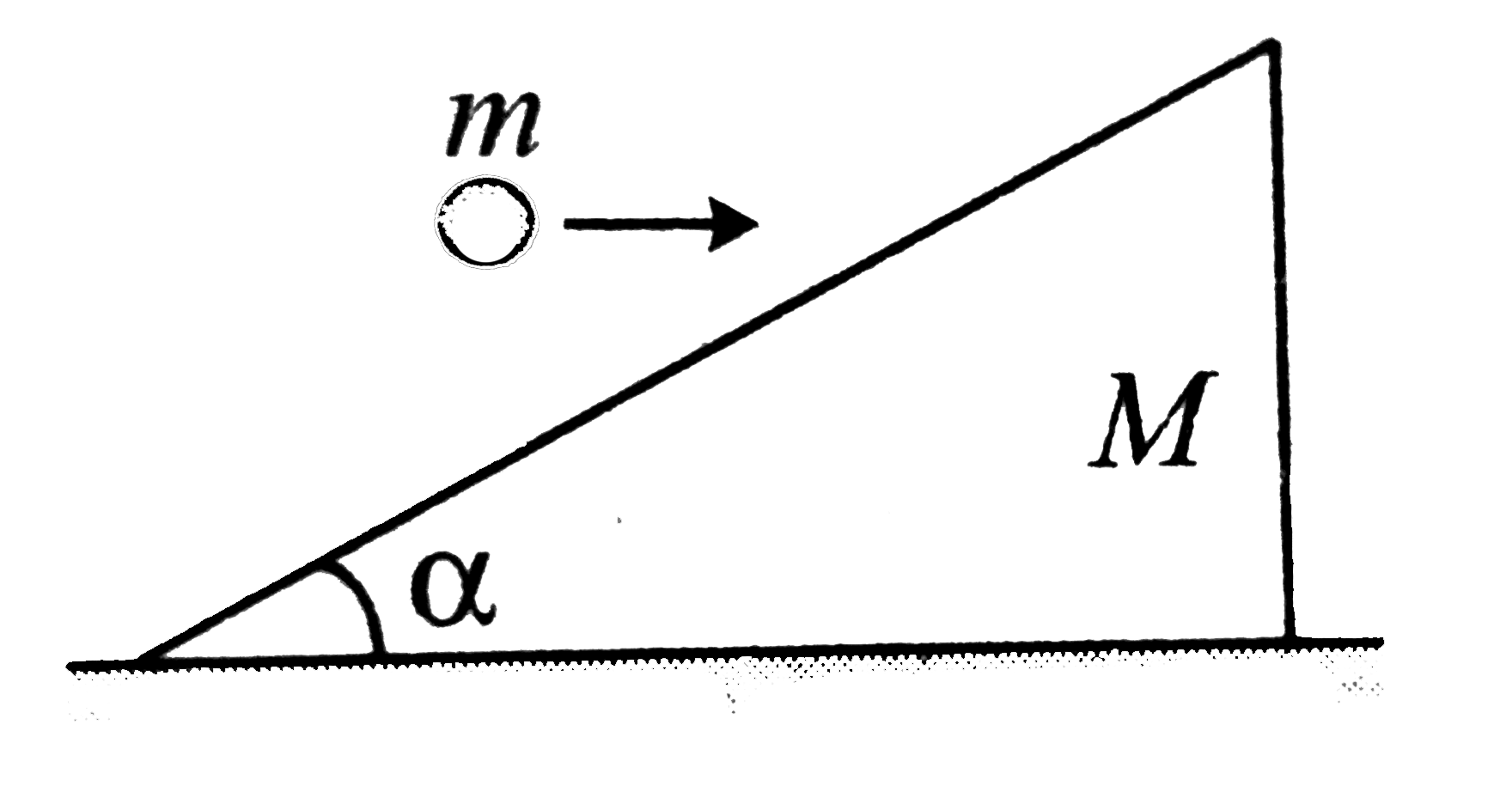
A ball of mass m moving with constant horizontal velocity u strikes a stationary wedge of mass M on its inclined surface as shown in the figure. After collision, the ball starts moving up the inclined plane. The wedge is placed on frictionless horizontal surface.
a. Calculate the velocity of wedge immediately after collision.
b. Calculate the maximum height the ball can ascend on the wedge.
View SolutionA small particle of mass m=2kg moving with constant horizontal velocity u=10m/s strikes a wedge shaped block of mass M=4kg placed on smooth horizontal surface on its inclined surface as shown in figure. After collision particle starts moving up the inclined plane. Calculate the velocity of wedge immediately after collision.
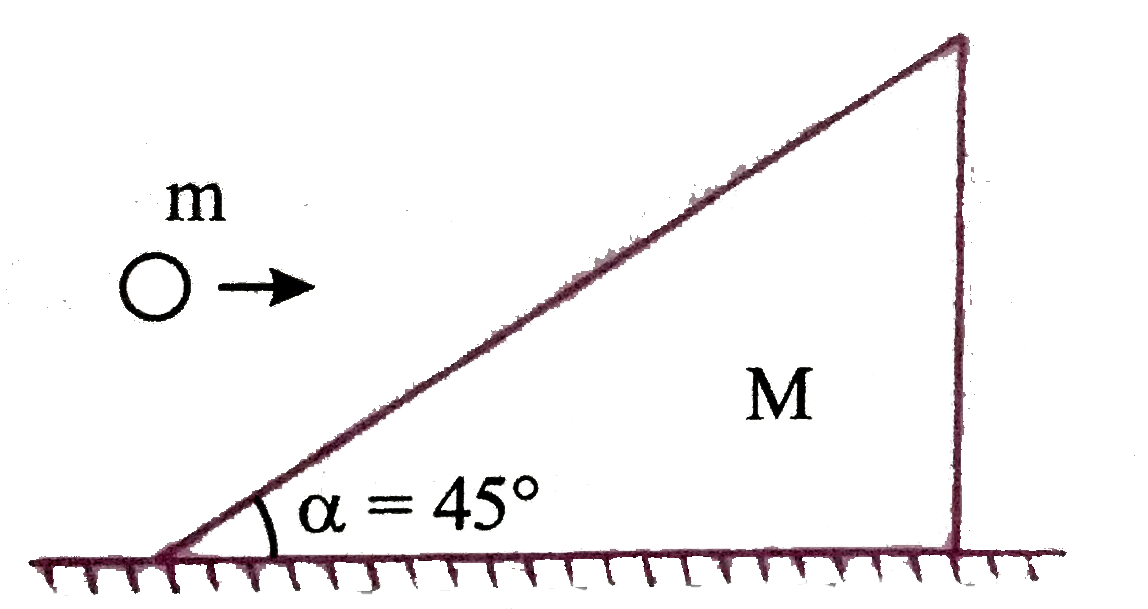
View SolutionA particle of mass m moving horizontal with v0 strikes a smooth wedge of mass M, as shown in figure. After collision, the ball starts moving up the inclined face of the wedge and rises to a height h.
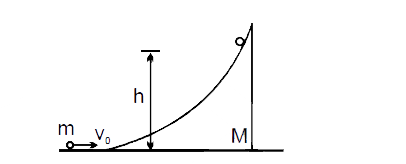
The maximum height h attained by the particle is
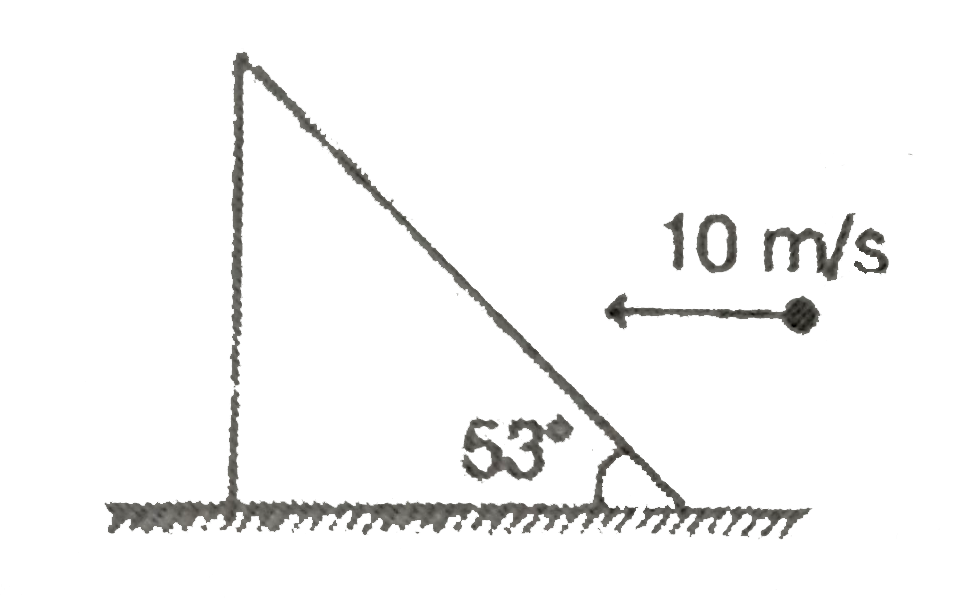
View SolutionA ball mass 2 kg moving horizontally with velocity 10 m/s hits a wedge of mass 5 kg placed on a horizontal surface as shown in the figure. Just after collision klvelocity of wedge is 3.2 m/s. There is no friction at any contact surface. Then (take sin 30∘=3/5)
View SolutionA particle of mass m moving horizontal with v0 strikes a smooth wedge of mass M, as shown in figure. After collision, the ball starts moving up the inclined face of the wedge and rises to a height h.
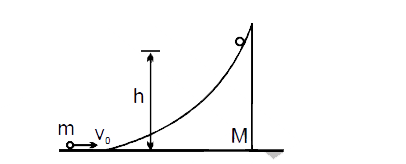
The final velocity of the wedgev2 is
View SolutionA particle of mass m moving horizontal with v0 strikes a smooth wedge of mass M, as shown in figure. After collision, the ball starts moving up the inclined face of the wedge and rises to a height h.
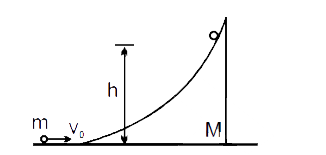
Choose the correct statement related to the wedge M
View SolutionA particle of mass m moving horizontal with v0 strikes a smooth wedge of mass M, as shown in figure. After collision, the ball starts moving up the inclined face of the wedge and rises to a height h.
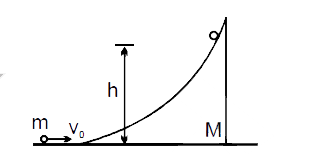
Choose the correct statement(s) related to particle m
View SolutionA ball of mass m=1kg falling vertically with a velocity v0=2m/s strikes a wedge of mass M=2kg kept o a smooth, horizontal surface as shown in figure. The coefficient of resitution between the ball and the wege is e=1/2. Find the velocity of the wedge is e=1/2. find the velocity of the wedge and the ball immediately after collison.
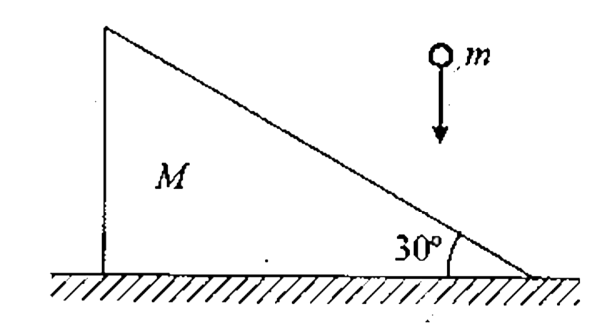
View SolutionA particle of mass m moving horizontal with v0 strikes a smooth wedge of mass M, as shown in figure. After collision, the ball starts moving up the inclined face of the wedge and rises to a height h.
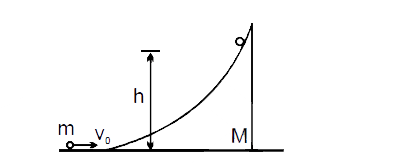
Identify the correct statement(s) related to the situation when the particle starts moving downward
View SolutionA particle of mass m moving horizontal with v0 strikes a smooth wedge of mass M, as shown in figure. After collision, the ball starts moving up the inclined face of the wedge and rises to a height h.
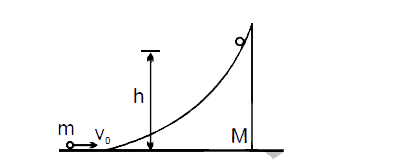
When the particle has risen to a height h on the wedge, then choose the correct alternative(s)
View Solution
