A body of mass 1kg initially at rest, explodes and breaks into three fragments of masses in the ratio 1:1:3. The two pieces of equal mass fly off perpendicular to each other with a speed of 15ms−1 each. What is the velocity of the heavier fragment?
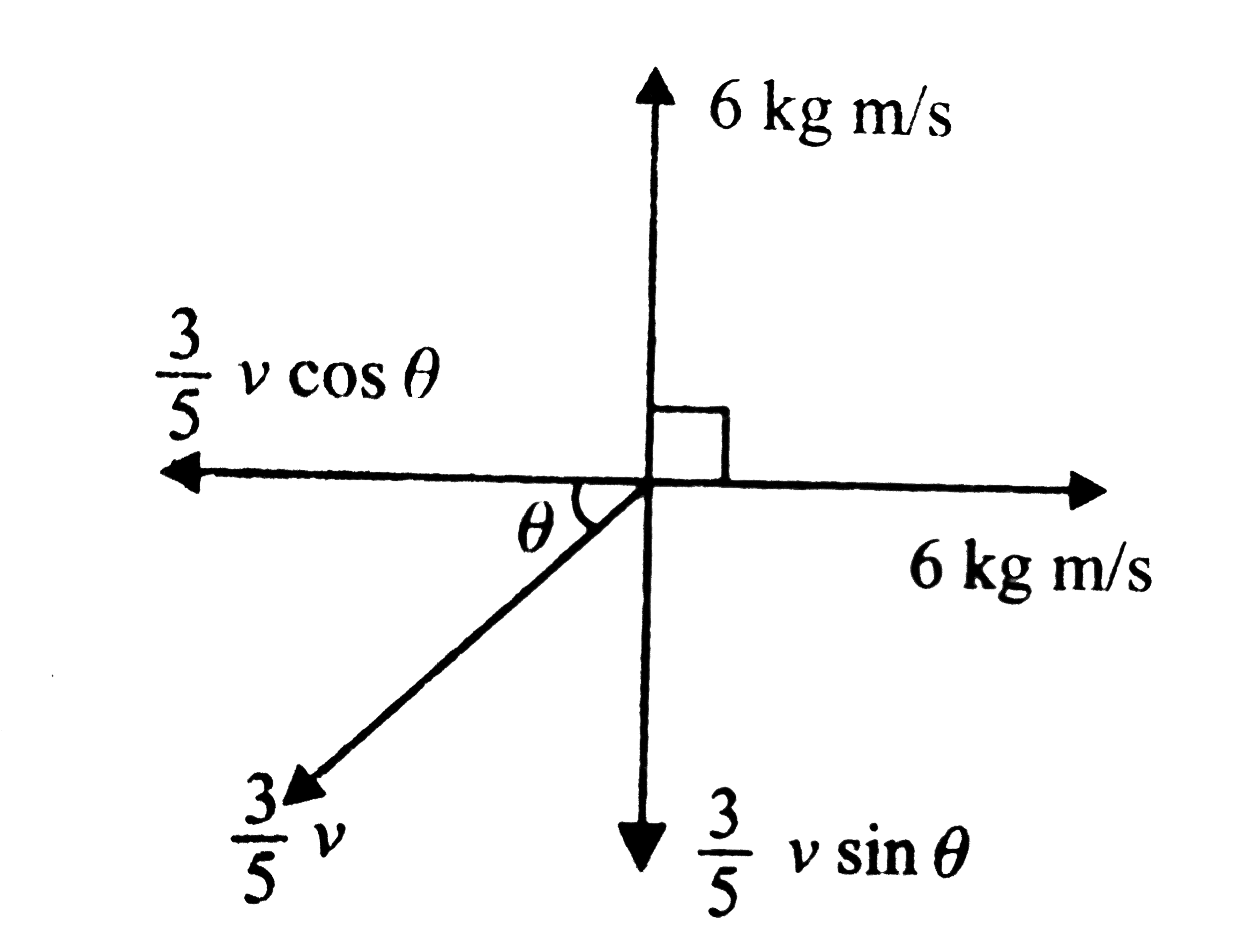
The momentum of the system is zero before explosion. Since the momentum is zero initially, it will be zero just after explosion according to conservation of linear momentum (as there is no external force acting on the system). The resultant momentum of the fragments flying off perpendicular to each other should be equal and opposite to the third fragment. Masses of fragments are 1/5kg,1/5kg and 3/5kg. Momentum of each of the smaller fragments is 15×30=6kgm/s.
Applying the principle of conservation of linear momentum in both the directions, we get
6=35vsinθ .............i
6=35cosθ ...................ii
squaring and adding we get 36+36=925v2
∴v=10√2m/s
Dividing the two equations, we get
tanθ=1, or θ=45∘
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Exercise 1.120videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Exercise 1.223videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - INTEGER_TYPE1videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICSCHAPTER - CALORIMETRYEXERCISE - Solved Example13videos
CALORIMETRY
- BOOK - CENGAGE PHYSICSCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer2videos
DIMENSIONS & MEASUREMENT
Similar Questions
A body of mass 1 kg initially at rest explodes and breaks into three fragments of masses in the ratio 1: 1: 3. The two pieces of equal mass fly off perpendicular to each other with a speed of 30ms−1 each. What is velocity of the heavier fragment?
View SolutionA bomb of mass 5m initially at rest explodes and breaks into three pieces of masses in the ratio 1:1:3. The two pieces of equal mass fly off perpendicular to each other with a speed of v0. What is the velocity of the heavier piece? Also , calculate the energy released in explosion.
View Solution
Knowledge Check
- Question 1 - Select One
A body of mass 1kg initially at rest explodes and breaks into three parts of masses in the ration 1:2:3. If the two pieces of equal masses fly off perpendicular to each other with a speed of 30m/s The speed of third piece will be .
A10√2m/sB20√2m/sC5√2m/sD40√2m/s - Question 2 - Select One
A body of mass 5 kg explodes at rest into three fragments with masses in the ratio 1 : 1 : 3. The fragments with equal masses fly in mutually perpendicular directions with speeds of 21 m/s. The velocity of the heaviest fragment will be -
A11.5 m/sB14.0 m/sC7.0 m/sD9.89 m/s - Question 3 - Select One
A body of mass 5 kg explodes at rest into three fragments with masses in the ratio 1 : 1 : 3. The fragments with equal masses fly in mutually perpendicular directions with speeds of 21 m/s . The velocity of the heaviest fragment will be
A11.5 m/sB14.0 m/sC7.0 m/sD9.89 m/s
A body of mass 1kg initially at rest explodes and breaks into threee fragments of masses in the ration breaks into three fragments of masses in the ration 1:1:3. The two pieces of equal masses fly off perpendicular to each other with a speed of 30m/s each What is the velocity of heavier fragments ? .
View SolutionA body of mass 1 kg at rest explodes into three fragments of masses in the ratio 1 : 1 : 3 . The two pieces of equal mass fly in mutually perpendicular directions with a speed of 30m/s each . What is the velocity of the heavier fragment ?
View SolutionA mass3in,initially at rest at the origin, explodes into three fragments of equal mass. Two of the fragments have speed v each and move perpendicular to each other. The third fragment will, move with a speed.
View SolutionA body of mass explodes at rest break up into three parts.If two parts having equal masses fly off perpendicularly to each other with a velocity of 18m/s, then calculate the velocilty of the third part which has a mass 3 times the mass of each part.
View SolutionA shell of mass m is at rest initially. It explodes into three fragments having masses in the ratio 2:2:1. The fragments having equal masses fly off along mutually perpendicular directions with speed v. What will be the speed of the third (lighter) fragment ?
View Solution

