A ball of mass moving with constant velocity u collides with a smooth horizontal surface at O as shown in Fig. Neglect gravity and friction. The y-axis is drawn normal to the horizontal surface at the point of impact O and x-axis is horizontal as shown. About which point will the angular momentum of ball be conserved?
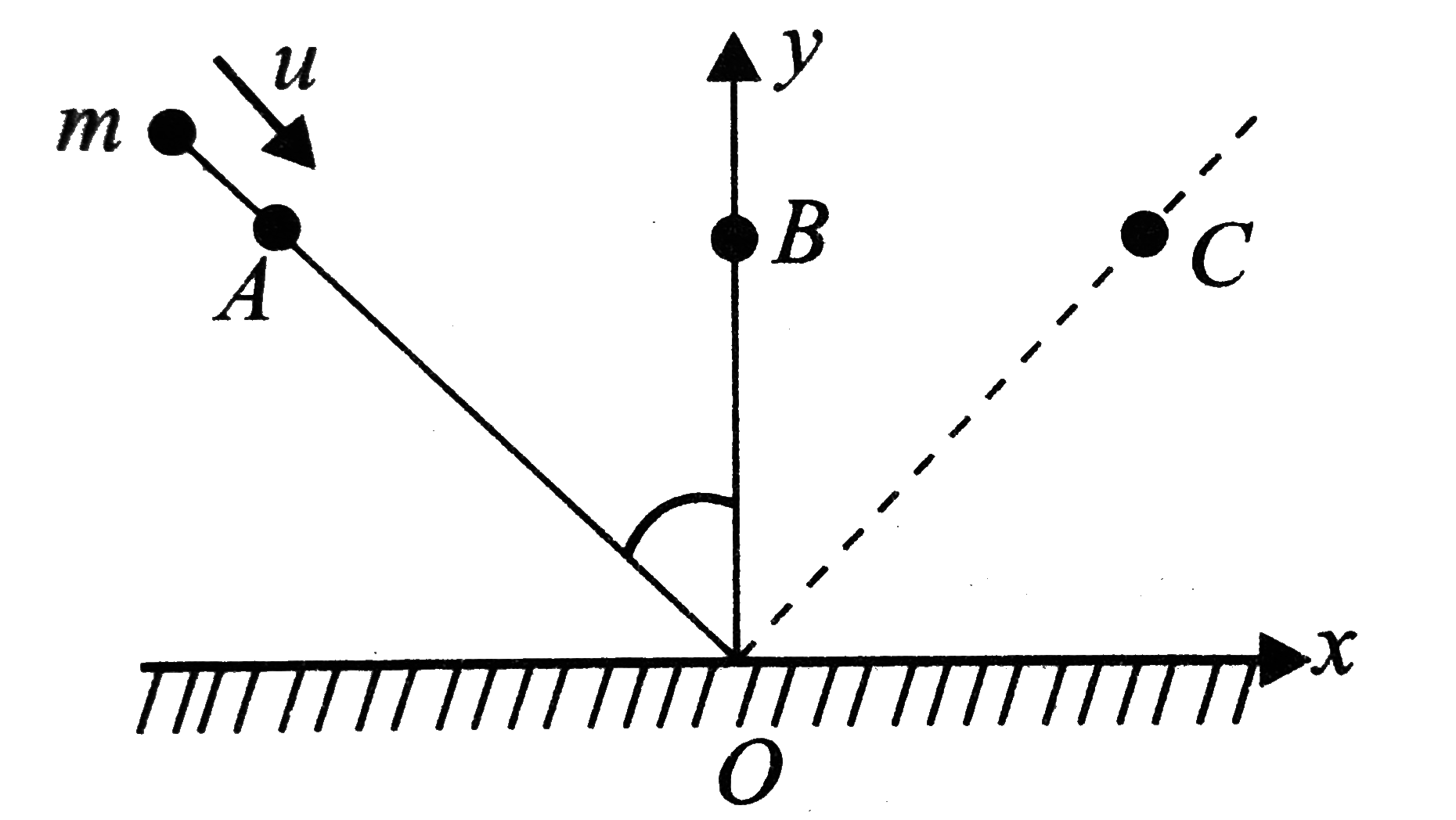
Point A
Point B
Point C
none of the above
The correct Answer is:B
As the normal force exerted by the horizontal surface passes through point B the external torque on the ball is zero about point B. So the angular momentum of the ball is conserved about point B (∵τ=dldt)
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Multiple Correct
26 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Linked Comprehension
71 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Subjective
19 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICSCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
Similar Questions
A ball moving with speed v collides with a horizontal smooth surface at an angle θ with normal to surface as shown in figure. If coefficient of restitution of collision is e, then find v'

View SolutionA ball is moving with speed 20ms−2 collides with a smooth surface as shown in figure. The magnitude of change in velocity of the ball will be

View Solution
Knowledge Check
A ball of mass m moving with speed u collides with a smooth horizontal surface at angle θ with it as shown in figure. The magnitude of impulse imparted to surface by ball is [Coefficient of restitution of collision is e]
 Amu(1+e)cosθBmu(1−e)sinθCmu(1−e)cosθDmu(1+e)sinθ
Amu(1+e)cosθBmu(1−e)sinθCmu(1−e)cosθDmu(1+e)sinθA block of mass m moving with velocity v0 on a smooth horizontal surface hits the spring of constant k as shown. Two maximum compression in spring is
 A√2mkv0B√mk.v0C√mk.v0Dm2k.v0
A√2mkv0B√mk.v0C√mk.v0Dm2k.v0A ball of mass m moving with velocity v, collide with the wall elastically as shown in the figure. After impact the change in angular momentum about P is :
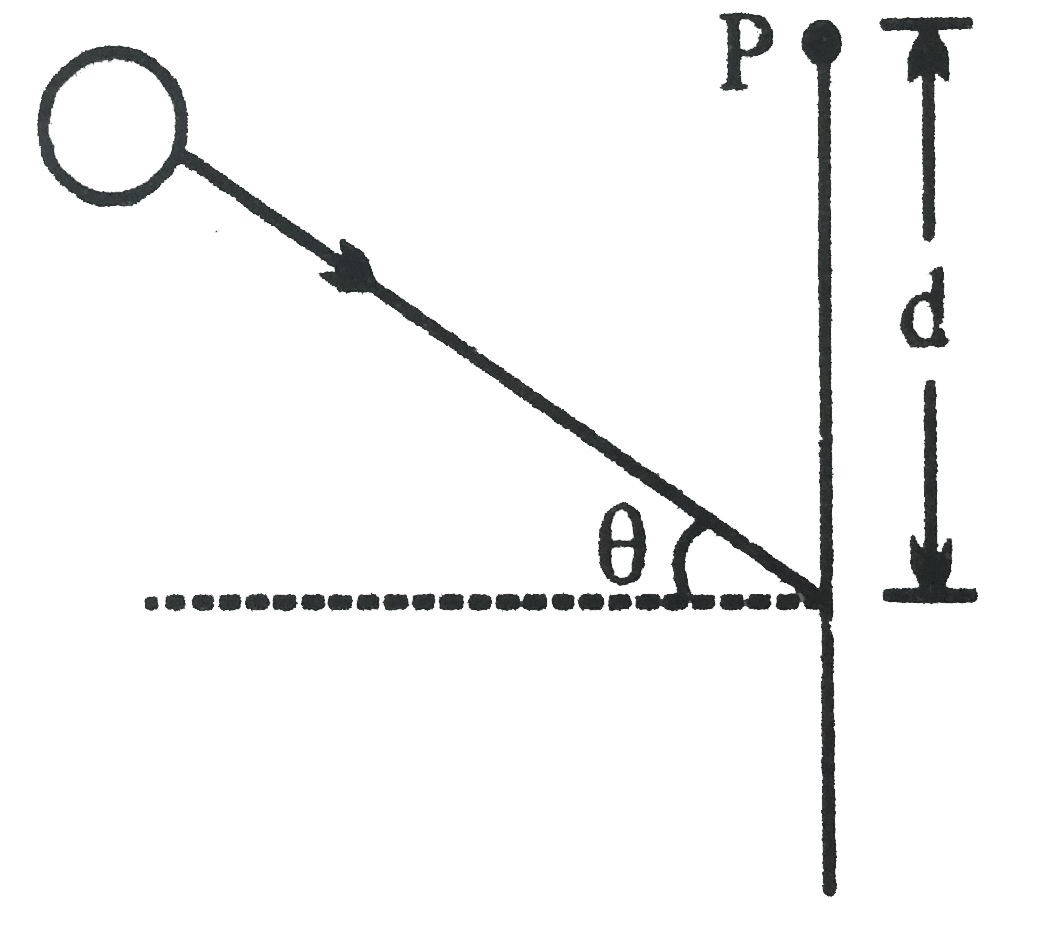 .A2mvdB2mvdcosθC2mvdsinθDzero
.A2mvdB2mvdcosθC2mvdsinθDzero
A particle of mass m is moving with constant velocity v parallel to the x-axis as shown in the figure. Its angular momentum about origin O is

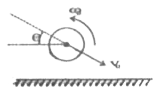
View SolutionA solid spherical ball of radius R collides with a rough horizontal surface as shown in figure. At the time of collision its velocity is v0 at an angle θ to the horizontal and angular velocity ω0 as shown . After collision, the angular velocity of ball may
View SolutionA particle is moving in a horizontal uniform circular motion. The angular momentum of the particle is conserved about the point :
View SolutionA cubical block of side a is moving with velocity V on a horizontal smooth plane as shown in Figure. It hits a ridge at point O. The angular speed fo the block after it hits O is
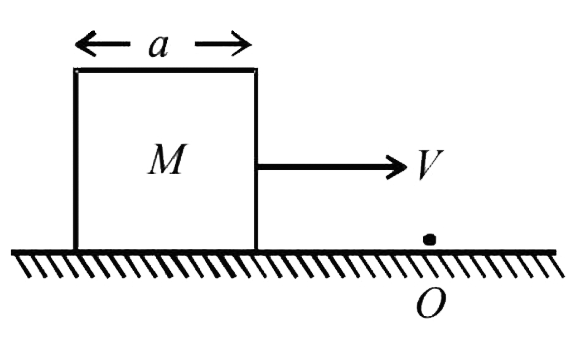
View SolutionA cubical block of side a is moving with velocity v on a horizontal smooth palne as shown . It hits a ridge at point O. The angular sped of the block after it hits O is
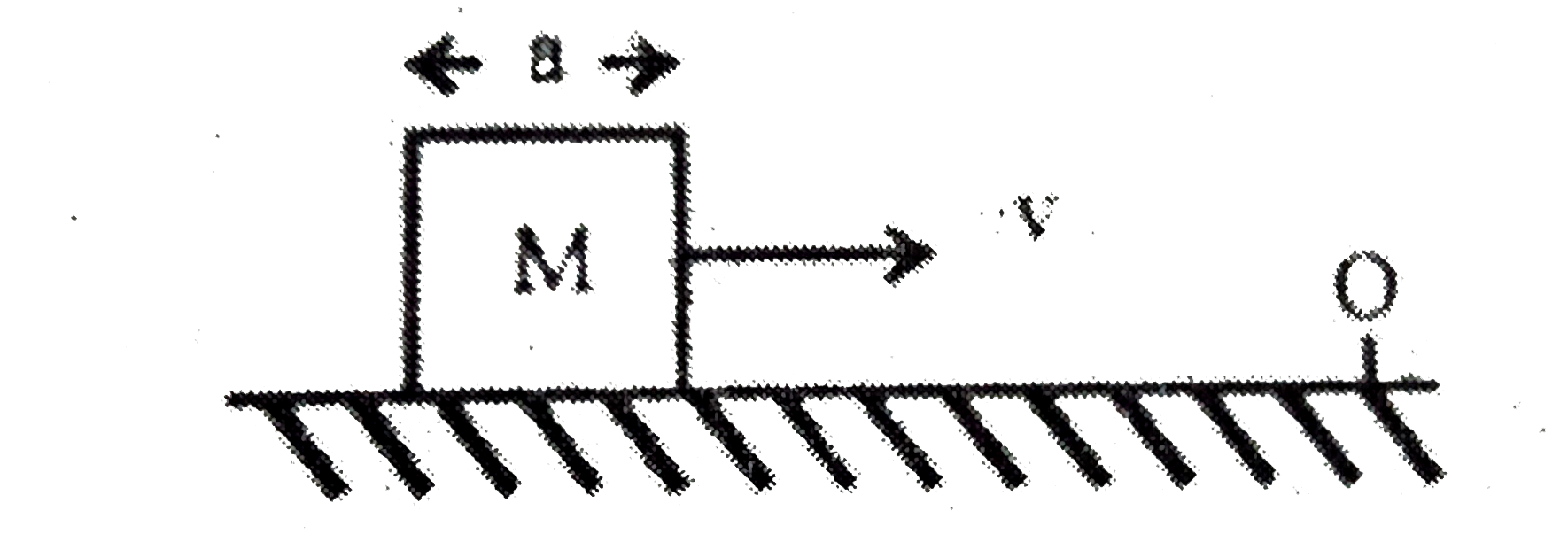
View Solution