A solid spherical ball of radius R collides with a rough horizontal surface as shown in figure. At the time of collision its velocity is v0 at an angle θ to the horizontal and angular velocity ω0 as shown . After collision, the angular velocity of ball may
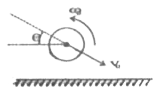
decrase
increase
remains constant
none of these
The correct Answer is:A
Step by step video, text & image solution for A solid spherical ball of radius R collides with a rough horizontal surface as shown in figure. At the time of collision its velocity is v_(0) at an angle theta to the horizontal and angular velocity omega_(0) as shown . After collision, the angular velocity of ball may by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- KINEMATICSBOOK - FIITJEECHAPTER - KINEMATICSEXERCISE - SECTION (II) : (SUBJECTIVE )
33 Videos
- KINEMATICSBOOK - FIITJEECHAPTER - KINEMATICSEXERCISE - SECTION(II) : MCQ ( SINGLE CORRECT)
47 Videos
- KINEMATICSBOOK - FIITJEECHAPTER - KINEMATICSEXERCISE - NUMERICAL BASED QUESTIONS
3 Videos
- HEAT AND TEMPERATUREBOOK - FIITJEECHAPTER - HEAT AND TEMPERATUREEXERCISE - NUMERICAL BASES QUESTIONS
1 Videos
- LAWS OF MOTIONBOOK - FIITJEECHAPTER - LAWS OF MOTIONEXERCISE - COMPREHENSION-III
2 Videos
Similar Questions
_S01_038_Q01.png)
As per the shown figure the central solid cylinder starts with initial angular velocity ω0 Find the time after which the angular velocity becomes half.
View SolutionA uniform solid sphere of mass m and radius r = 3m is projected along a rough horizontal surface with the initial velocity v0=6m/s and angular ω0 velocity as shown in the figure. If the sphere finally comes to complete rest then angular velocity is x rad/s. Find x.
View Solution
Knowledge Check
A projectile is projected with a velocityv0 at an angle θ with the horizontal as shown in figure. The angular momentum of particle about the origin:
Ais zero when particle is at the originBis −mv3sin2θcosθ2gˆk when particle is at the highest point of trajectoryCis −2mv2sin2θcosθgˆk when particle is just about to hit groundDdownward force of gravity exerts a torque in −z direction.A point mass m collides with a disc of mass m and radius R resting on a rough horizontal surface as shown . Its collision is perfectly elastic. Find angular velocity of the disc after pure rolling starts
A(2u3R)B(3u3R)C(5u3R)D(2u5R)A uniform circular disc of radius r is placed on a rough horizontal surface and given a linear velocity v0 and angular velocity ω0 as shown. The disc comes to rest after moving some distance to the right. It follows that
A3v0=2ω0rB2v0=ω0rCv0=ω0rD2v0=3ω0r
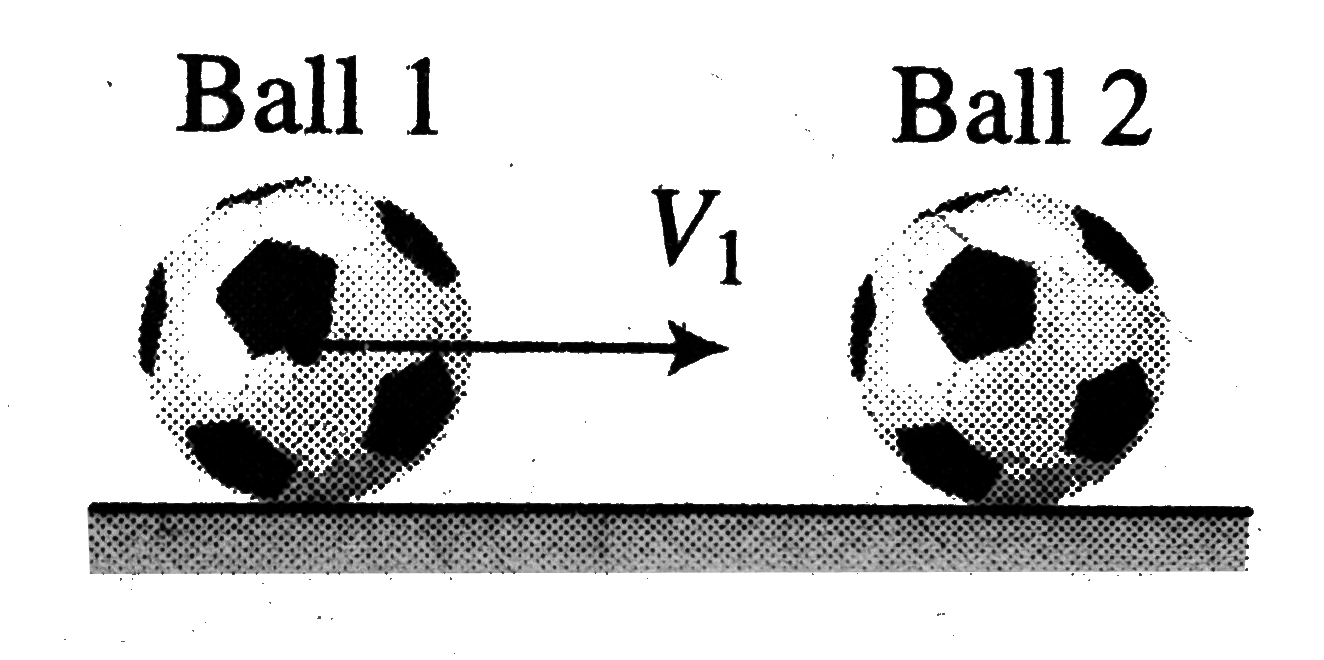
A solid spherical ball rolling without slipping collides elastically with an identical ball at rest, as shown in the figure. Assuming that the frictional forces are small enough to have negligible effect during the instant of collision, calculate, the velocity of each ball along enough time after the collision when each ball is again rolling without slipping.
View SolutionA solid sphere of radius R is set into motion on a rough horizontal surface with a linear speed v0 in forward direction and an angular with a linear speed v0 in forward direction and an angular velocity ω0=v0/2R in counter clockwise direction as shown in figure. If coefficient of friction μ then find
a. the time after which sphere starts pure rolling,
b. the linear speed of sphere when it starts rolling and
c. the work down by friction over a long time.
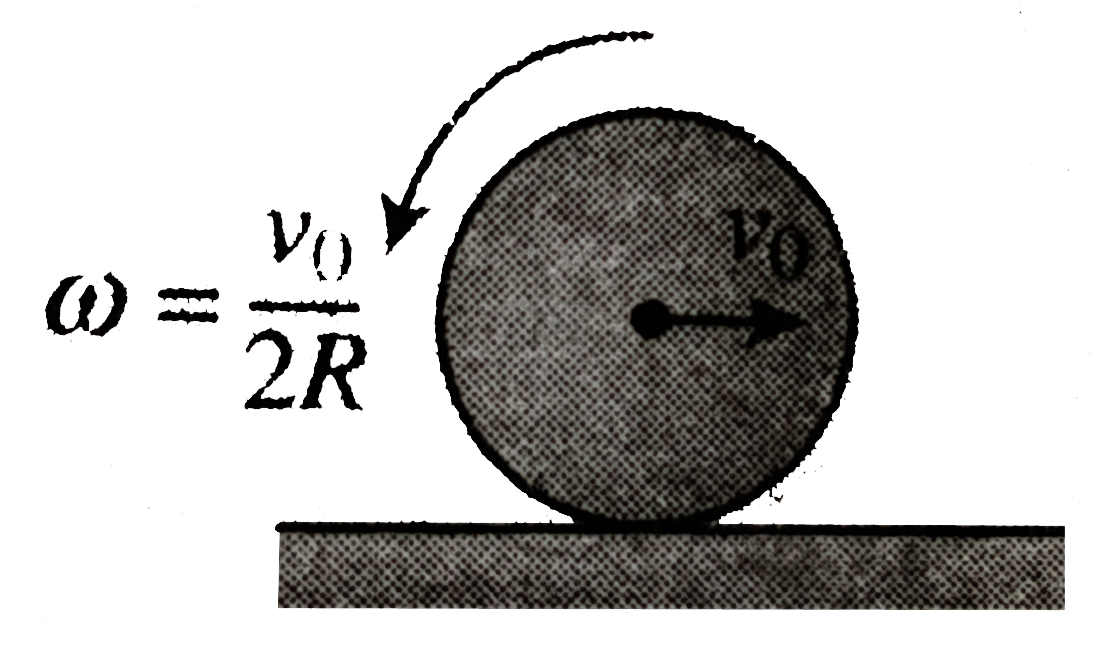
View SolutionA uniform solid sphere of radius R, rolling without sliding on a horizontal surface with an angular velocity ω0, meets a rough inclined plane of inclination θ=60∘. The sphere starts pure rolling up the plane with an angular velocity ω Find the value of ω.
View SolutionA ball is projected horizontal from the top of a tower with a velocity v0. It will be moving at an angle of 60∘ with the horizontal after time.
View SolutionA uniform disc of mass m and radius R is released gentiy on a horizontal rough surface. Such that centre of the disc has velocity V0 towards right and angular velocity ω0 (anticlockwise) as shown.
Disc will certainly come back to its intial position if
View Solution