A ball of radius r fits tightly inside a tube attached to a container. There is no friction between the tube wall and the ball. Volume of air inside the container is V0 when the ball is in equilibrium. Density of the material of the ball is d and atmospheric pressure is P0. If the ball is displaced a little from its equilibrium position and released, find time period of its oscillation. Assume that temperature in the container remains constant and that air is an ideal gas.
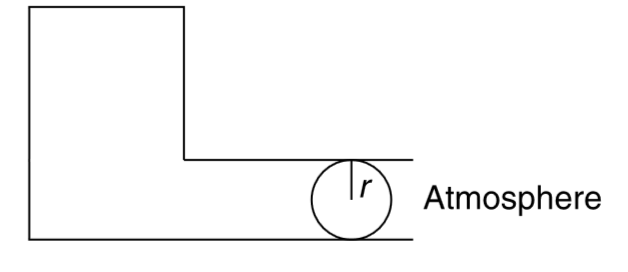
The correct Answer is:T=4√πV0d3P0r
Topper's Solved these Questions
- FIRST LAW OF THERMODYNAMICSBOOK - ARIHANTCHAPTER - FIRST LAW OF THERMODYNAMICSEXERCISE - Level 3
6 Videos
- FIRST LAW OF THERMODYNAMICSBOOK - ARIHANTCHAPTER - FIRST LAW OF THERMODYNAMICSEXERCISE - Level 3
6 Videos
- ELASTICITYBOOK - ARIHANTCHAPTER - ELASTICITYEXERCISE - Level 3
1 Videos
- FLUIDSBOOK - ARIHANTCHAPTER - FLUIDSEXERCISE - All Questions
70 Videos
Similar Questions
A spherical ball is placed between a vertical wall and a movable inclined plane as shown. There is no friction between the wall and the ball, and no friction between the ball and the inclined plane. The coefficient of friction between the inclined plane and the ground is The system is in equilibrium.

The normal force exerted by the plane on the ball is
View SolutionA box contains 7 red balls, 8 green balls and 5 white balls. A ball is drawn at random from the box. Find the probability that the ball is white.
View Solution
Knowledge Check
A solid ball is exactly fitted inside the cubical box of side a. The volume of the ball is .
A13πa3B43πa3C16πa3Dcan not be determinedA ball floats on the surface of water in a container exposed to the atmosphere. Volume V1 of its volume is inside the water. The container is now covered and the air is pumped out. Now let V2 be the volume immersed in water. Then
AV1=V2BV1>V2CV2>V1DV2=0A ball of mass 5 kg hanging from a spring oscillates with a time period of 2πs. At any instant the ball is at equilibrium position, now the ball is removed, then spring shortens by
A2πmB9/2mC9.8mD2 m
A ball rises to the surface of a liquid with constant velocity. The density of the liquid is four time the density of the material of the ball. The frictional force of the liquid on the rising ball is greater than the weight of the ball by a factor of
View SolutionA ball floats on the surface of water in a container exposed to the atmosphere. Volume V1 of its volume is inside the water. The container is now covered and the air is pumped out. Now let V2 be the volume immersed in water. Then
View SolutionA ball of mass M and radius R is released on a rough inclined plane of inclination θ. Friction is not sufficient to prevent slipping. The coefficient friction between the ball and the plane is μ. Find
(a). The linear acceleration of the ball down the plane.
(b). the angular acceleration of the ball about its centre of mass.
View SolutionA ball of mass M and radius R is released on a rough inclined plane of inclination θ. Friction is not sufficient to prevent slipping. The coefficient friction between the ball and the plane is μ. Find
(a). The linear acceleration of the ball down the plane.
(b). the angular acceleration of the ball about its centre of mass.
View SolutionThere is a long vertical tube of radius r containing air at atmospheric pressure. A steel ball is held at the mouth of the tube and dropped. The ball has radius r and it just fits inside the tube. The tube wall is perfectly smooth and no air can leak from the tube as the ball falls inside it. The ball falls through half the length of the tube before coming to rest. Assume that wall of the tube is perfectly conducting and temperature of the air inside the tube remains constant. Density of steel is d and atmospheric pressure is P0 and take L>>r. Take air to be an ideal gas.
(a) Find the radius (r) of the tube.
(b) At what depth from the top of the tube the ball will be in equilibrium?
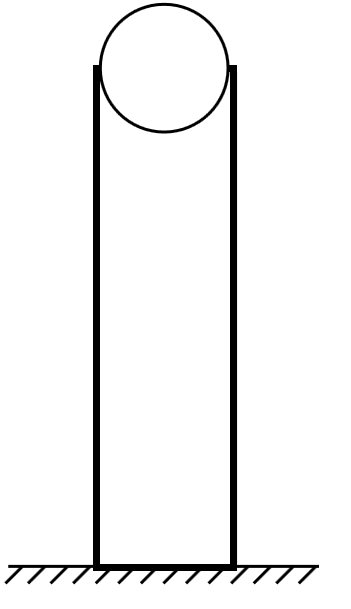
View Solution
