Figure shows P versus V graph for various processes performed by an ideal gas. All the processes are polytropic following the process equation PVk= constant.
(i) Find the value of k for which the molar specific heat of the gas for the process is CP+CV2. Does any of the graph given in figure represent this process?
(ii) Find the value of k for which the molar specific heat of the gas is CV+CP. Assume that gas is mono atomic. Draw approximately the P versus V graph for this process in the graph given above.
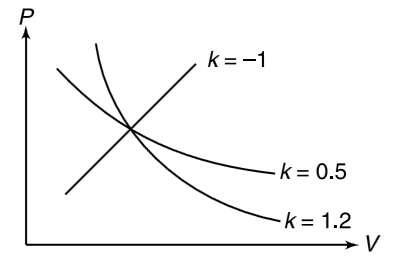
The correct Answer is:(i)k=−1 (ii)k=0.6
Step by step video, text & image solution for Figure shows P versus V graph for various processes performed by an ideal gas. All the processes are polytropic following the process equation PV^(k) = constant. (i) Find the value of k for which the molar specific heat of the gas for the process is (C_(P)+C_(V))/(2). Does any of the graph given in figure represent this process? (ii) Find the value of k for which the molar specific heat of the gas is C_(V) + C_(P). Assume that gas is mono atomic. Draw approximately the P versus V graph for this process in the graph given above. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- FIRST LAW OF THERMODYNAMICSBOOK - ARIHANTCHAPTER - FIRST LAW OF THERMODYNAMICSEXERCISE - Level 3
6 Videos
- FIRST LAW OF THERMODYNAMICSBOOK - ARIHANTCHAPTER - FIRST LAW OF THERMODYNAMICSEXERCISE - Level 3
6 Videos
- ELASTICITYBOOK - ARIHANTCHAPTER - ELASTICITYEXERCISE - Level 3
1 Videos
- FLUIDSBOOK - ARIHANTCHAPTER - FLUIDSEXERCISE - All Questions
70 Videos
Similar Questions
Find the value of molar heat capacity for an ideal gas in an adiabatic process.
View SolutionFor an ideal gas the ratio of specific heats is CpCv=γ. The gas undergoes a polytropic process PV^(n) = a constant. Find the values of n for which the temperature of the gas increases when it rejects heat to the surrounding.
View Solution
Knowledge Check
P-V graph for an ideal gas undergoing polytropic process PVm=constant is shown here. Find the value of m.
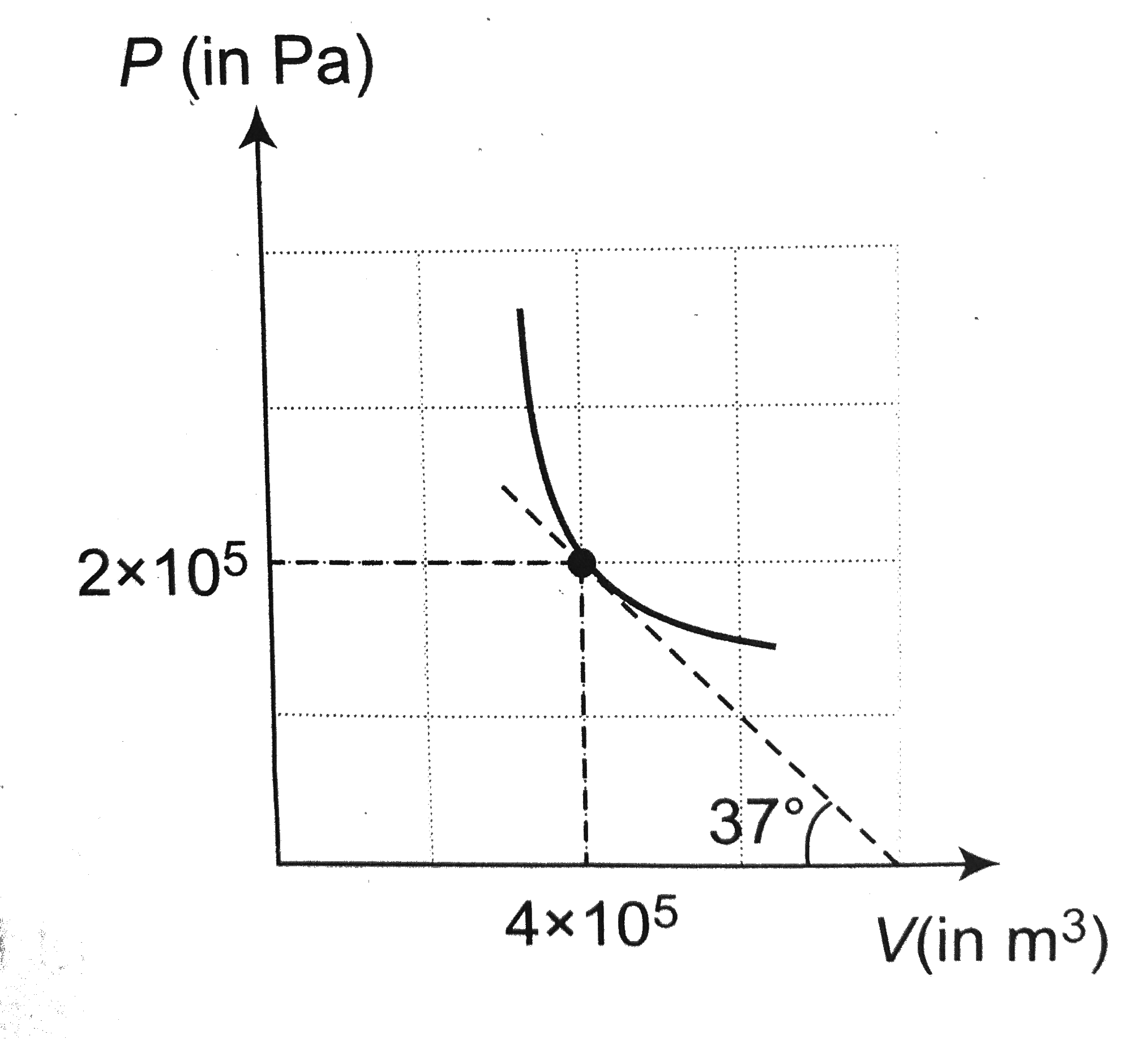 A34B−32C53D32
A34B−32C53D32A certain amount of ideal monoatomic gas undergoes a process given by TV1/2= constant. The molar specific heat of the gas for the process will be given by
AR/2B−3R/2C3R/2D−R/2A polytropic process for an ideal gas is represented by equation PVn=constant. If g is ratio of specific heats (CpCv), then value of n for which molar heat capacity of the process is negative is given as
Aγ>nBγ>n>1Cn>γDnone, as it is not possible
One mole of a diatomic gas undergoes a thermodynamic process, whose process equation is P∝V2. The molar specific heat of the gas is
View SolutionAn ideal diatomic gas undergoes a process in which the pressure is proportional to the volume. Calculate the molar specific heat capacity of the gas for the process.
View SolutionFind the molar specific heat of the process p=aT for a monoatomic gas, a being constant.
View SolutionOne mole of an ideal monoatomic gas undergoes a process as shown in the figure. Find the molar specific heat of the gas in the process.
R is a gas constant.
View SolutionFigure demonstrates a polytropic process (i.e.PVn = constant ) for an ideal gas. The work done by the gas be in the process AB is
_S01_086_Q01.png)
View Solution
