A ball projected from ground vertically upward is at same height at time $t_{1} and t_{2}$ . The speed of projection of ball is [Neglect the effect of air resistance ]

$\frac{g (t_{1} + t_{2})}{2}$ q

$\frac{g (t_{1} - t_{2})}{2}$

$g (t_{1} + t_{2})$

$g (t_{1} - t_{2})$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:a

A particle projected from ground moves at angle $45^{\circ}$ with horizontal one second after projection and speed is minimum two seconds after the projection The angle of projection of particle is [ Neglect the effect of air resistance )
A ${tan}^{- 1} (3)$
B ${tan}^{- 1} (2)$
C ${tan}^{- 1} (\sqrt{2})$
D ${tan}^{- 1} (4)$
A particle is projected vertically upward and is at a height h after $t_{1}$ seconds and again after $t_{2}$ seconds
A $h = {gt}_{1} t_{2}$
B $h = \frac{1}{2} {gt}_{1} t_{2}$
C $h = \frac{2}{g} t_{1} t_{2}$
D $h = \sqrt{{gt}_{1} t_{2}}$
Two stones are projected from level ground. Trajectory of two stones are shown in figure. Both stones have same maximum heights above level ground as shown. Let $T_{1}$ and $T_{2}$ be their time of flights and $u_{1}$ and $u_{2}$ be their speeds of projection respectively (neglect air resistance). then

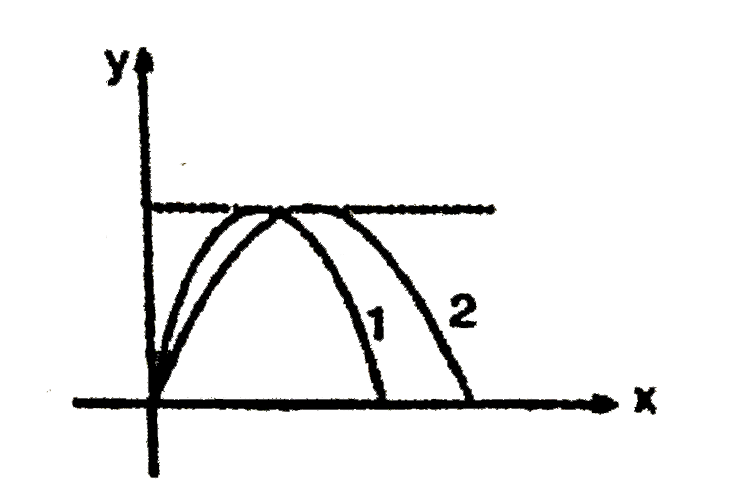A $T_{2} > T_{1}$
B $T_{1} = T_{2}$
C $u_{1} > u_{2}$
D $u_{1} = u_{2}$