A particle is thrown up with an initial velocity such that it takes more than one second to reach the top point. What is the distance travelled by the particle during the first second of its decent?
g/2
g/4
g
Information is insufficient to calculate the desired distance.
The correct Answer is:a
To solve the problem step by step, we will analyze the motion of the particle thrown upwards and then its descent.
Step 1: Understanding the Motion
When a particle is thrown upwards with an initial velocity, it moves against the gravitational force until it reaches its highest point (the top point). The time taken to reach this top point is given as more than one second.
Step 2: Time of Ascent and Descent
Let’s denote the time taken to reach the top point as t. Since it takes more than one second to reach the top, we can say t>1 seconds. The motion is symmetrical, meaning the time taken to ascend is equal to the time taken to descend. Thus, the time taken to descend from the top point back to the ground is also t seconds.
Step 3: Distance Covered in the Last Second of Ascent
To find the distance covered by the particle during the first second of its descent, we need to determine the distance it covered in the last second of its ascent. The last second of ascent occurs between t−1 seconds and t seconds.
Step 4: Using the Equation of Motion
The distance covered during the last second of ascent can be calculated using the equation of motion:
S=ut+12at2
Where:
- S is the distance,
- u is the initial velocity,
- a is the acceleration (which is −g for upward motion),
- t is the time.
For the last second of ascent (from t−1 to t):
- The distance covered in the last second can be expressed as:
S=u(t)−u(t−1)+12(−g)(12)
This simplifies to:
S=u−(u−g(t−1))−12g
S=g(t−1)−12g
Step 5: Distance During Descent
Due to the symmetry of motion, the distance covered during the first second of descent will be equal to the distance covered during the last second of ascent. Therefore, the distance traveled during the first second of descent is:
S=12g
Step 6: Final Calculation
Assuming g≈9.8m/s2:
S=12×9.8≈4.9meters
Conclusion
The distance traveled by the particle during the first second of its descent is approximately 4.9 meters.
---
When a particle is thrown upwards with an initial velocity, it moves against the gravitational force until it reaches its highest point (the top point). The time taken to reach this top point is given as more than one second.
Let’s denote the time taken to reach the top point as t. Since it takes more than one second to reach the top, we can say t>1 seconds. The motion is symmetrical, meaning the time taken to ascend is equal to the time taken to descend. Thus, the time taken to descend from the top point back to the ground is also t seconds.
To find the distance covered by the particle during the first second of its descent, we need to determine the distance it covered in the last second of its ascent. The last second of ascent occurs between t−1 seconds and t seconds.
The distance covered during the last second of ascent can be calculated using the equation of motion:
S=ut+12at2
Where:
- S is the distance,
- u is the initial velocity,
- a is the acceleration (which is −g for upward motion),
- t is the time.
- The distance covered in the last second can be expressed as:
S=u(t)−u(t−1)+12(−g)(12)
This simplifies to:
S=u−(u−g(t−1))−12g
S=g(t−1)−12g
Due to the symmetry of motion, the distance covered during the first second of descent will be equal to the distance covered during the last second of ascent. Therefore, the distance traveled during the first second of descent is:
S=12g
Assuming g≈9.8m/s2:
S=12×9.8≈4.9meters
The distance traveled by the particle during the first second of its descent is approximately 4.9 meters.
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - COMPETITION FILE ( B.(MULTIPLE CHOICE QUESTIONS))74videos
MOTION IN A STRAIGHT LINE
- BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - COMPETITION FILE ( C.(MULTIPLE CHOICE QUESTIONS))13videos
MOTION IN A STRAIGHT LINE
- BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - REVISION EXERCISE (NUMERICAL PROBLEMS )7videos
MOTION IN A STRAIGHT LINE
- BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - Chapter Practice Test15videos
MOTION IN A PLANE
- BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - Practice Test (For Board Examination)12videos
OSCILLATIONS
Similar Questions
From the velocity time plot shown in figure find the distance travelled by the particle dureing the first 40 seconds. Also find the average velocity during this period.
 View Solution
View SolutionThe variation of velocity of particle moving along a straight line is shown in the figure. The distance travelled by the particle in 4th second is?
View Solution
Knowledge Check
- Question 1 - Select One
If S=3t3+9t2+2t+7 , then distance travelled by the particle during the first second of its motion is
A7 unitsB21 unitsC14 unitsD28 units - Question 2 - Select One
A particle is thrown with any velocity vertically upward, the distance travelled by the particle in first second of its decent is
AgBg2Cg4DCannot be calculated - Question 3 - Select One
The motion of a particle is described by the equation at u=at.The distance travelled by the particle in the first 4 seconds
A4aB12aC6aD8a
The variation of velocity of particle moving along a straight line is shown in the figure. The distance travelled by the particle in 4th second is
View SolutionThe v-t graph for a particle is as shown. The distance travelled in the first seconds is :
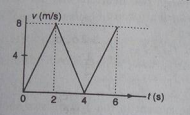 View Solution
View SolutionThe v-t graph for a particle is as shown. The distance travelled in the first seconds is :
 View Solution
View SolutionA body thrown vertically upwards with an initial valocity u reaches maximum height in 6 s. The ratio of the distances traveled by the body in the first second the seventh second is
View SolutionThe v−t graph for a particle is shown. The distance travelled in the first four seconds is:
 View Solution
View Solution

