A ball, rolling purely on a horizontal floor with centre's speed v, hits a smooth vertical wall surface elastically. Answer the following questions.

Just after the collision is over, the velocity of the lowest point of the ball is
v, leftward
2v, leftward
v, rightward
2v, rightward
The correct Answer is:B
Just after collision
v=ωr
Velocity of lowest potential =v+ωr=2v
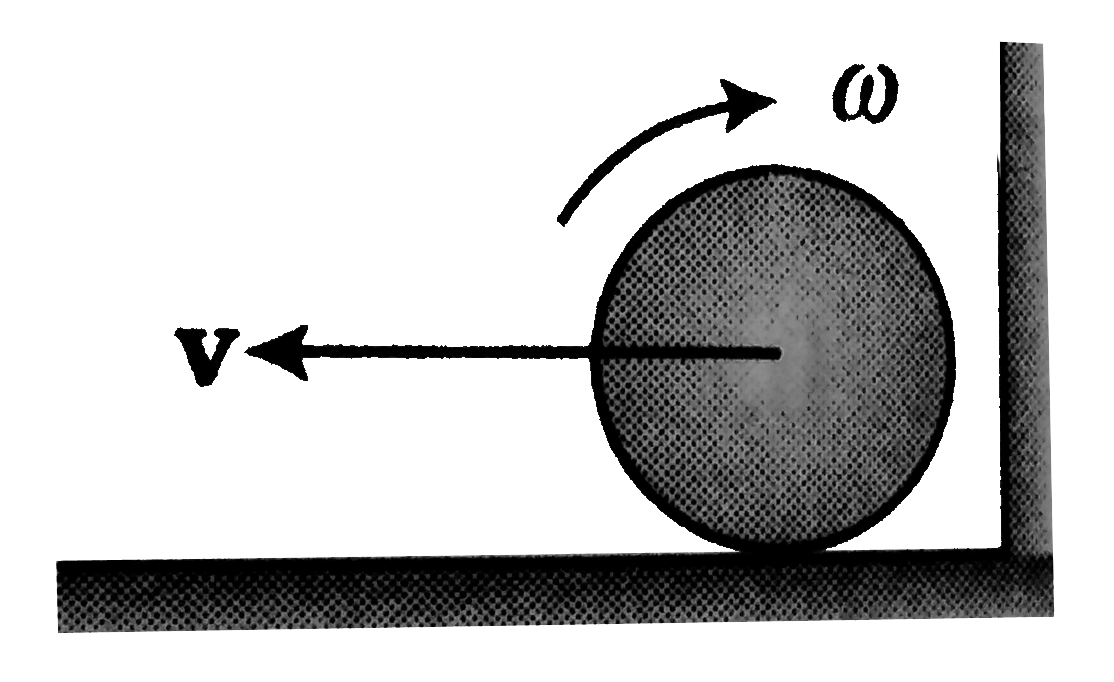
Change in angular momentum is due to translational part only, as ω does not change due to collision.
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Integer
7 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Fill In The Blanks
7 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Multiple Correct
26 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICSCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
Similar Questions
A sphere rolling on a horizontal rough surface Collides elastically with a smooth vertical wall, as shown in Fig. State which of the following statements is true or false.
 a. After collision, the velocity of the centre of mass gets reversed.
a. After collision, the velocity of the centre of mass gets reversed.
b. Angular momentum of the sphere about the point of contact with the wall is conserved.
c. Angular momentum of the sphere about a stationary point on the horizontal surface is conserved.
d. Just after collision the point of contact with the horizontal surface is moving towards the wall.
e. After collision the friction force acts on the sphere such that it decreases the linear speed and increases the angular speed.
f. Finally, when the sphere starts rolling, it is moving away from the wall.
View SolutionA ball rolls without sliding over a rough horizontal floor with velocity v0=7m/s towards a smooth vertical wall. If coefficient of restitution between the wall and the ball is e=0.7. Calculate velocity v of the ball long after the collision.
View Solution
Knowledge Check
A ball, rolling purely on a horizontal floor with centre's speed v, hits a smooth vertical wall surface elastically. Answer the following questions.
The change in angular momentum of the solid ball (mass m, radius R), about the corner point of floor and wall, due to the collision isA2mvRBmvRCmvR/2Dnone of theseA ball is projected on a very long floor. There may be two conditions (i) floor is smooth &(ii) the collision is elastic
If both the considered then the path of ball is as follows.

Now if collision is inelastic and surface is rough then the path is as follows.

Successive range is decreasing .
Roughness of surface decreases the horizontal component of ball during collision and inelastic nature of collision decreases the vertical component of velocity of ball. In first case both components remain unchanged in magnitude and in second case both the components of the velocity will change.
Let us consider a third case here surface is rough but the collision of ball with floor is elastic. A ball is projected withe speed u at an angle 30∘ with horizontal and it is known that after collision with the floor its speed becomes u√3 . Then answer the following questions.
If the ball after first collision with the floor has rebounded vertically then the speed of the ball just after the collision with the floor would have been :AuBu/2C√32DNone of theseA ball moving with speed v hits another identical ball at rest. The two balls stick together after collision. If specific heat of the material of the balls is S , the temperature rise resulting from the collision is
Av28sBv24SCv22SDv2S
A ball of radius R=20cm has mass m=0.75kg and moment of inertia (about its diameter ) I=0.0125kgm2. The ball rolls without sliding over a rough horizontal floor with velocity v0=10ms−1 towards a smooth vertical wall if coefficient of restitution between the wall and the ball is e=0.7, calculate velocity v of the ball long after the collision. (g=10ms−2)
View SolutionA ball moving on a horizontal frictionless plane hits an identical ball at rest with a velocity of 0.5m/s. If the collision is elastic, calculate the speed imparted to the target ball, if the speed of projectile after the collision is 30cm/s. Show that the two balls will move at right angles to eachother, after the collision.
View SolutionA wedge mass m rest on horizontal surface. The inclination of the wedge is α. A ball of mass m moving horizontal with speed u hits the inclined face of the wedge in elastically and after hitting slides up the inclined face of the wedge. Find the velocity of the wedge just after collision. Neglect any friction.
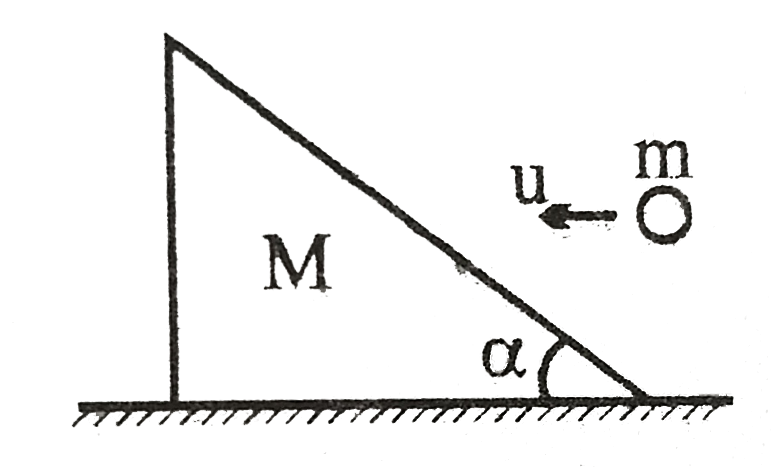
View SolutionA ball moving with velocity u strikes a smooth horizontal floor at an angle α with the normal to the surface at the point of contact . After collision , ball moves with velocity v at an angle β with the normal . Assume e as the coefficient of restitution .
View SolutionA ball moving with speed v hits another identical ball at rest. The two balls stick together after collision. If specific heat of the material of the balls is S , the temperature rise resulting from the collision is
View Solution
