A solid ball of mass m and radius r spinning with angular velocity ω falls on a horizontal slab of mass M with rough upper surface (coefficient of friction μ) and smooth lower surface. Immediately after collision the normal component of velocity of the ball remains half of its value just before collision and it stops spinning. Find the velocity (in m/s) of the sphere in horizontal direction immediately after the impact (given: Rω=5).
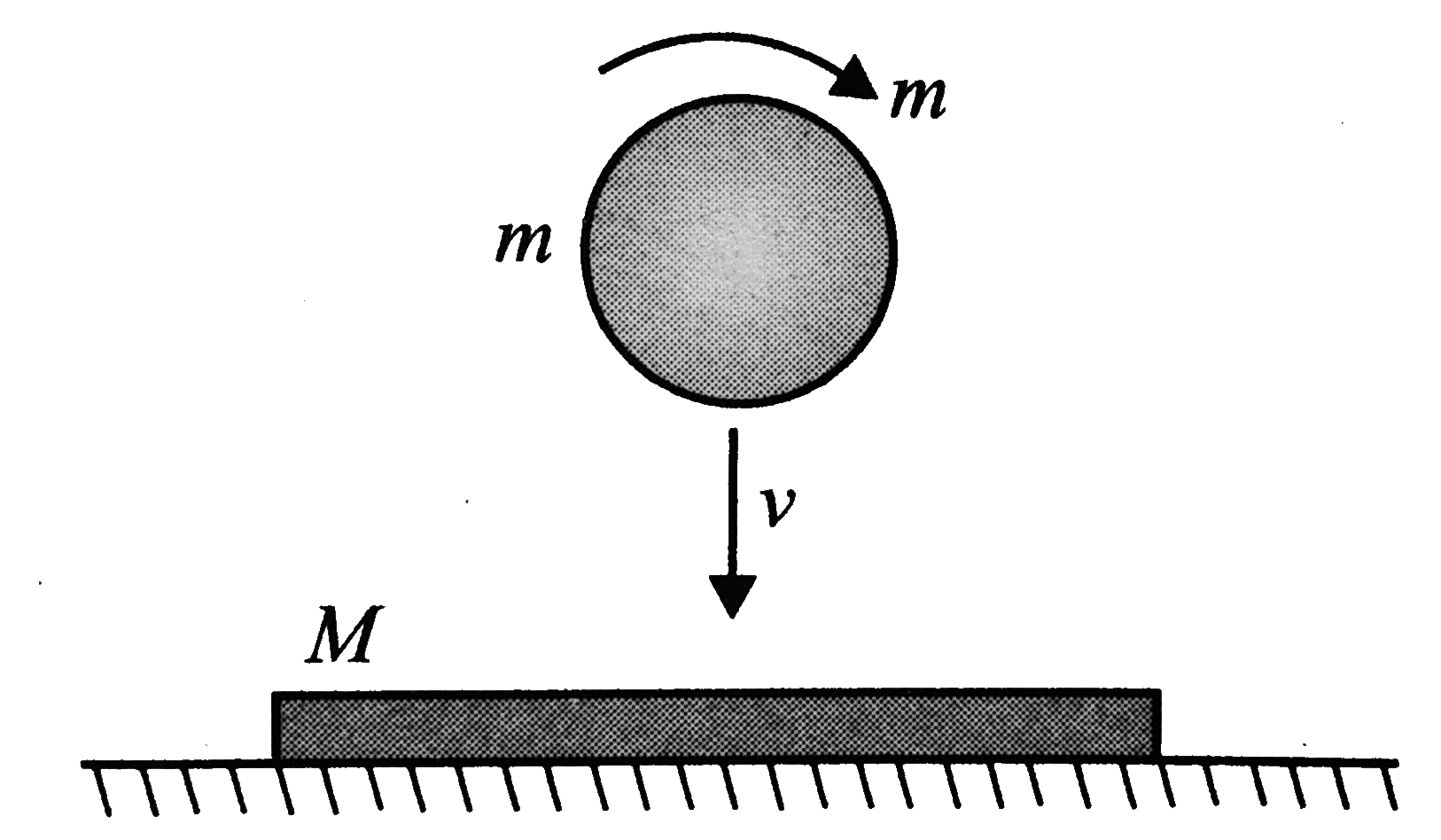
The correct Answer is:2
J=∫Ndt=mv2−(−mv)=32,mv………..i
μJR=∫μ(Ndt)R=(25mR2ω−0)=25mR2ω……..ii

From eqn i and ii we get
32mvrμ=25mR2ω……….iii
let V and V1 be the speeds of the plank and the sphere, respectively in the horizontal direction.
μJ=∫mjNdt=Mv=mV1........iv
Form eqn i and iv μ(32)mv=MV
V=32μmvM=32415mRωM=25Rω
and V1=25Rω=2m/s
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Integer
7 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Fill In The Blanks
7 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Multiple Correct
26 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICSCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
Similar Questions
A solid ball of mass m and radius r spinning with angular velocity ω falls on a horizontal slab of mass M with rough upper surface (coefficient of friction μ) and smooth lower surface. Immediately after collision the normal component of velocity of the ball remains half of its value just before collision and it stops spinning. Find the velocity (in m/s) of the sphere in horizontal direction immediately after the impact (given: Rω=5).

View SolutionA solid ball of mass m and radius r spinning with angular velocity ω falls on a horizontal slab of mass M with rough upper surface (coefficient of friction μ) and smooth lower surface. Immediately after collision the normal component of velocity of the ball remains half of its value just before collision and it stops spinning. Find the velocity of the sphere in horizontal direction immediately after the impact (given: Rω=5).

View Solution
Knowledge Check
A ring of radius R is first rotated with an angular velocity ω and then carefully placed on a rough horizontal surface. The coefficient of friction between the surface and the ring is μ. Time after which its angular speed is reduced to half is
Aω0μR2gBω0g2μRC2ω0RμgDω0R2μgA ball of mass m is projected with a velocity 'u' at angle θ with the horizontal. It collides with a smooth box of mass 'M' at its highest position. If the co-efficient of restitution is 'e'.
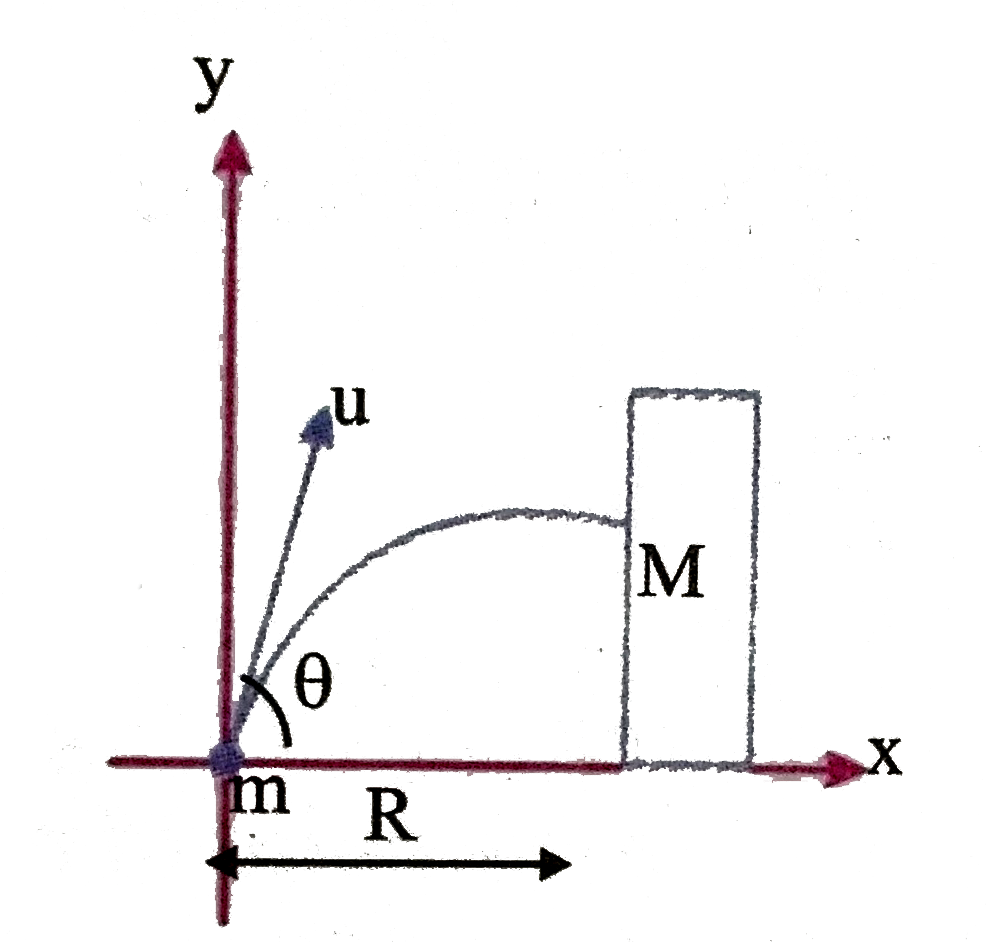
FInd the velocity of the ball after collisionA(m−eMM+m)ucosθB(M−emM+m)ucosθC(m+eMM+m)usinθD(m−eMM+m)usinθA ball of mass m moving with velocity v collides head-on which the second ball of mass m at rest. I the coefficient of restitution is e and velocity of first ball after collision is v1 and velocity of second ball after collision is v2 then
Av1=(1−e)u2,v2=(1+e)u2Bv1=(1+e)u2,v2=(1−e)u2Cv1=u2,v2=−u2Dv1=(1+e)u,v2=(1−e)u
A solid ball of mass m and radius R spinning with angular velocity ω falls on a horizontal slab of mass M with rough upper surface (coefficient of friction μ ) and smooth lower surface. Immediately after collision, the normal component of velocity of the ball becomes half of its value just before collision and it stops spinning. Find the velocity of the sphere in horizontal direction immediately after the impact (given :Rω=5 ).

View SolutionA ring of radius R is first rotated with an angular velocity ω and then carefully placed on a rough horizontal surface. The coefficient of friction between the surface and the ring is μ. Time after which its angular speed is reduced to half is
View SolutionA ball of mass m moving with velocity u collides head-on which the second ball of mass m at rest. If the coefficient of restitution is e and velocity of first ball after collision is v1 and velocity of second ball after collision is v2 then
View SolutionA ball of mass m moving with velocity v collides head-on which the second ball of mass m at rest. I the coefficient of restitution is e and velocity of first ball after collision is v1 and velocity of second ball after collision is v2 then
View SolutionA small ball of mass m collides with as rough wall having coefficient of friction μ at an angle θ with the normal to the wall. If after collision the ball moves with angle α with the normal to the wall and the coefficient of restitution is e, then find the reflected velocity v of the ball just after collision.
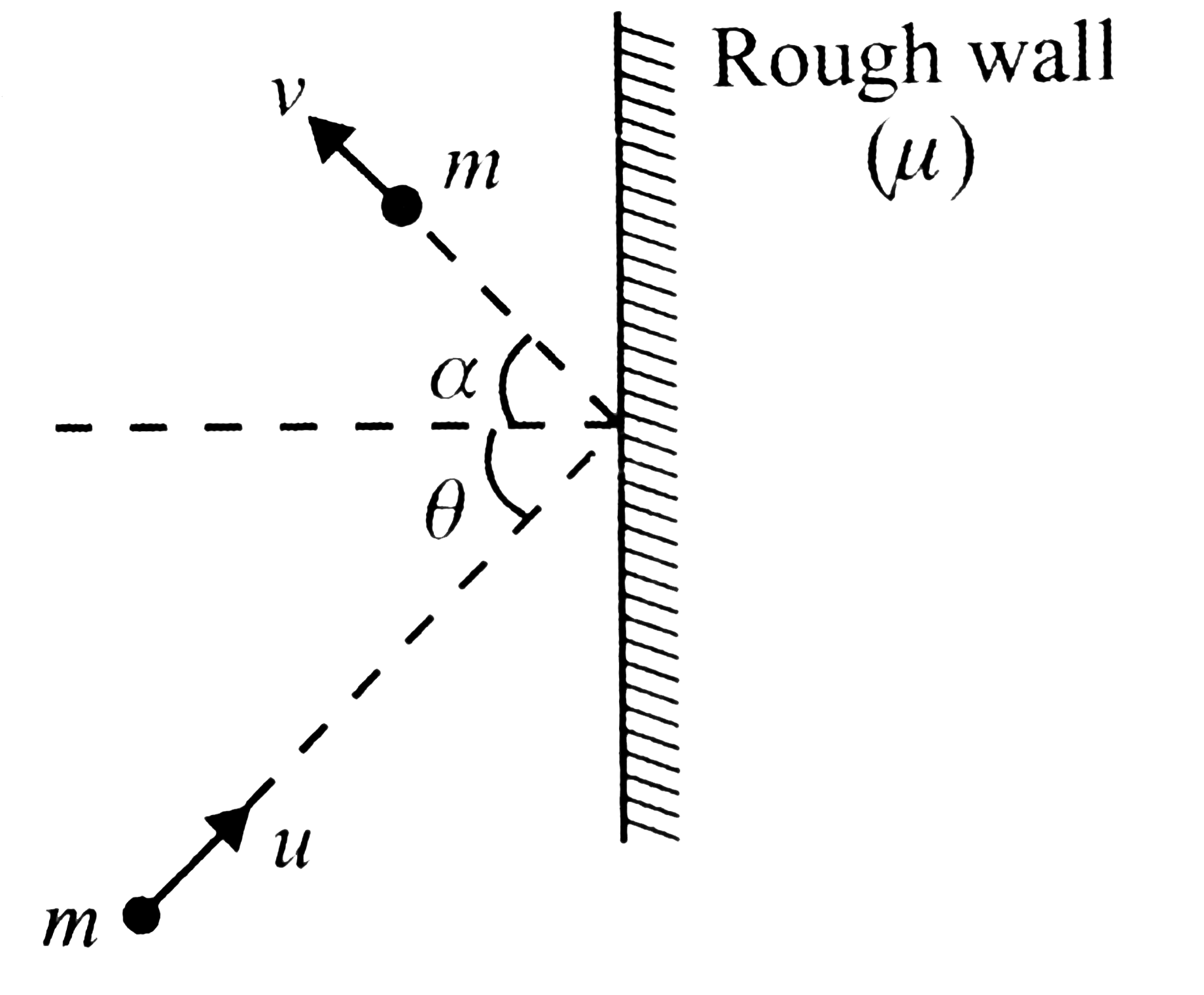
View Solution
