Question

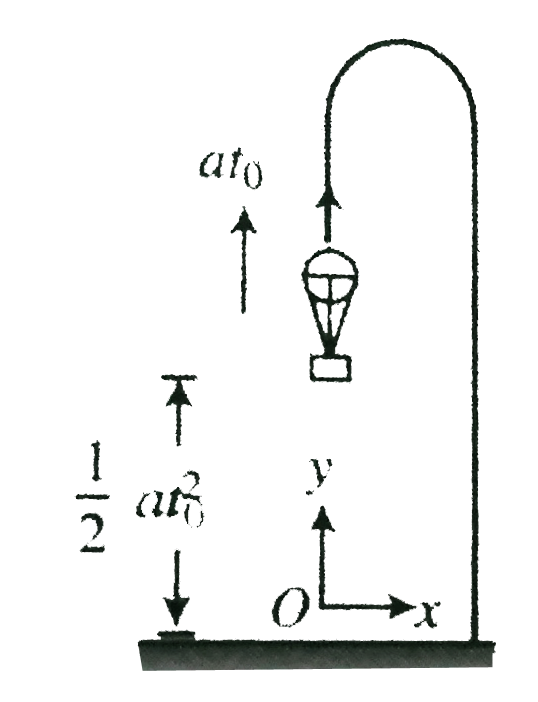
A ballon starts rising from ground from rest at some constant acceleration. After some time, a storne is dropped from it. If the stone reaches the ground in the same time in which balloon reached the dropping poing from ground, find the acceleration of the balloon.

Answer

`(g)/(3)`

Explanation

For balloon, `v=at` (i)
`S=(1)/(2)at^(2)` (ii)
For stone, -`S=vt-(1)/(2)g t^(2)` (iii)
From equation(i), (ii) and (ii)
`-(1)/(2)at^(2)=(at) t-(1)/(2)at^(2) rArr a=(g)/(3)`.