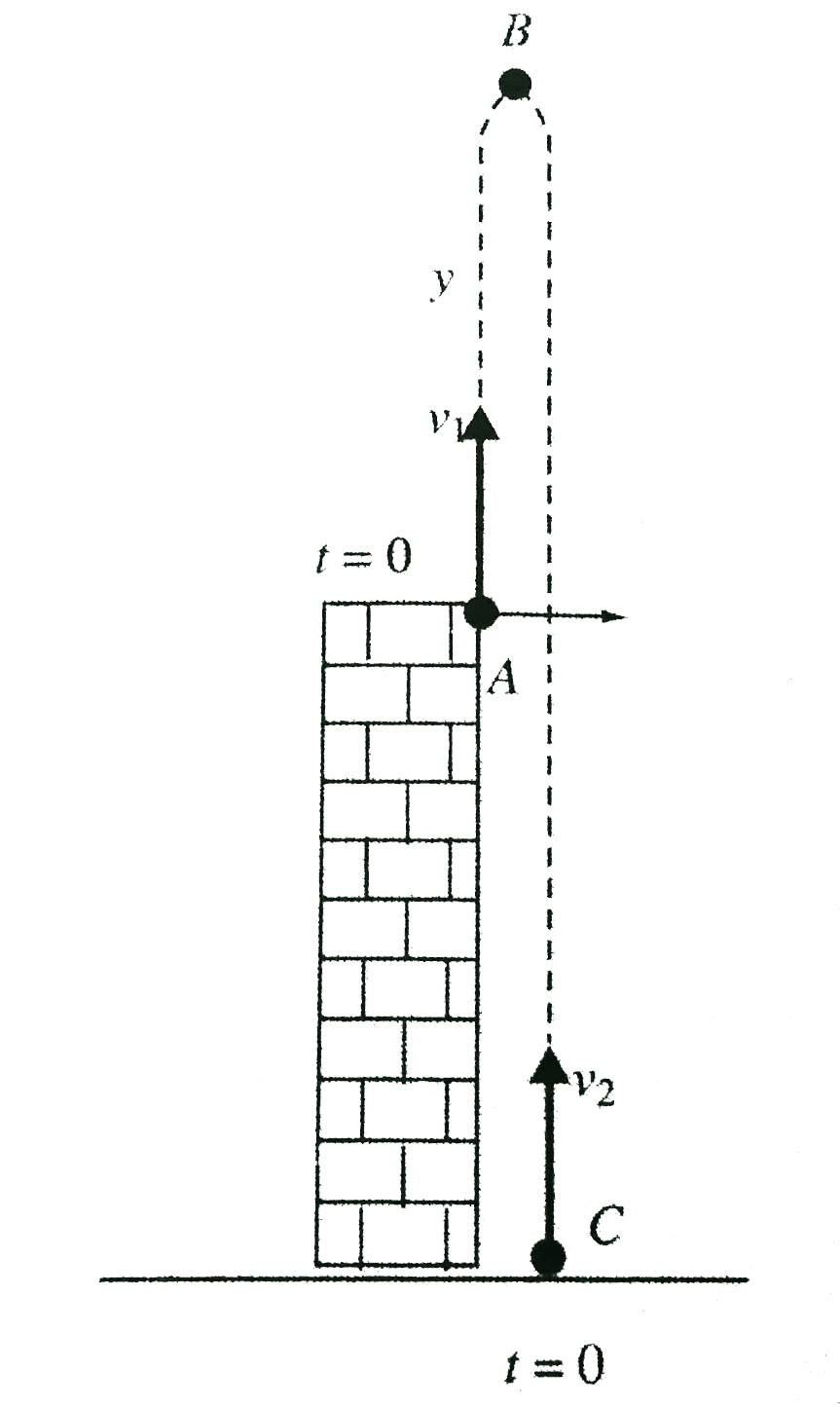
Two particles and are projected simultaneously with velocities and , respectively. Particle is projected vertically up from the top of a cliff of height and particle is projected vertically up from the bottom of the cliff. If the bodies meet (a) above the top of the cliff, (b) between the top and bottom of the the cliff, and (c ) below the bottom of the cliff, find the time of meeting of the particles.
 .
.
The correct Answer is:
Let the balls meer after a time measured form the instant of projection of the first ball. Since, the second ball is projected aftre a time from the instant of projection of the first ball, the second ball falls freely for a time .
If the balls meet between the top and bottom of the cliff, for the first ball, and
This yields (i)
For the second ball, and
Hence (ii)
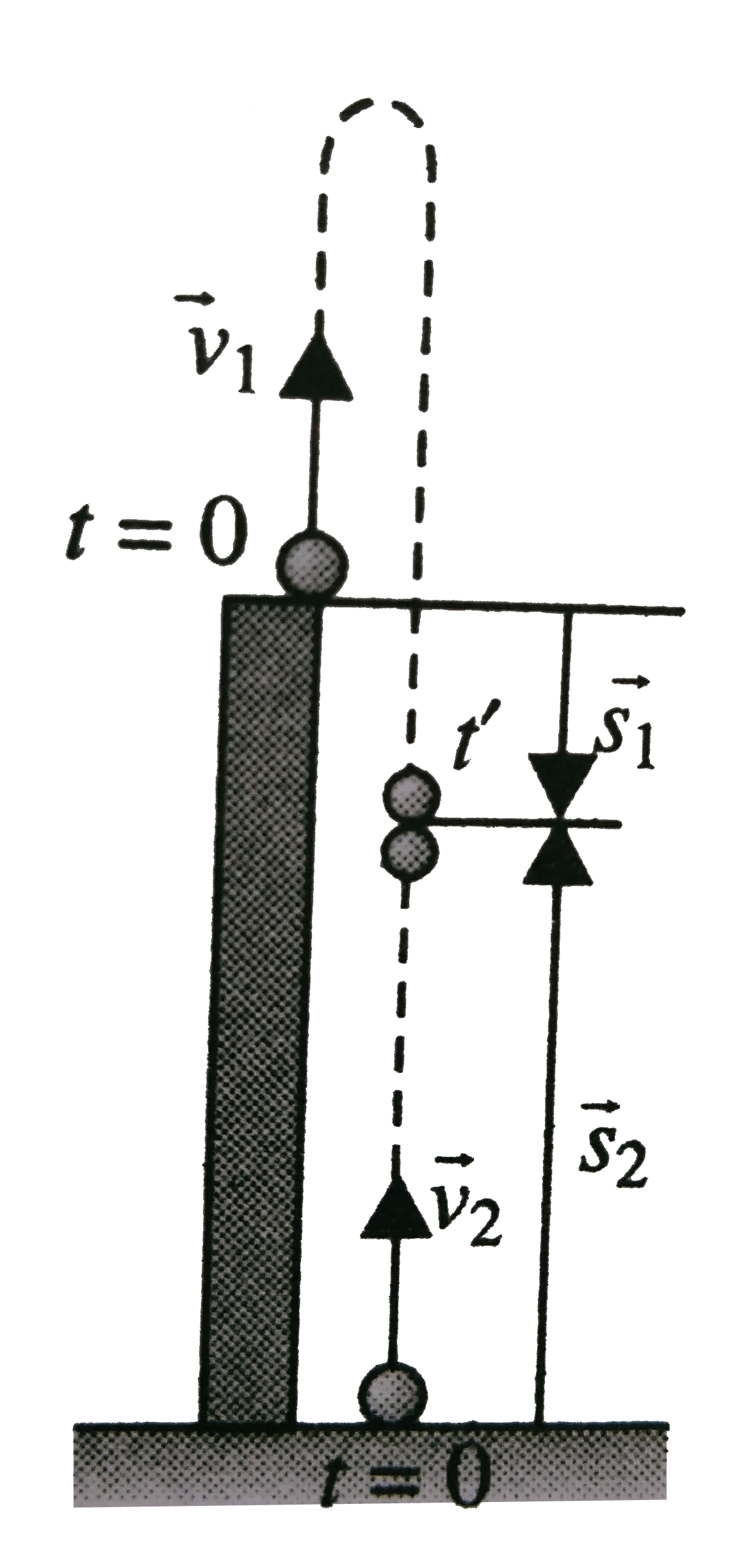
Referring tothe fig we have (iii)
Substituting from eq, (i). from eq. (ii) in eq, (iii), we havev_(1)t'+(1)/(2)g t'^(2) +v_(2)(t'-t_(0))-(1)/(2)-(1)/(2)g(t'-t_(0))^(2)=h t'=(2(h+v_(2)t_(0))+g t_(0)^(2))/(2{(v_(2)-v_(1))+g t_(0)})
 .
.
Topper's Solved these Questions
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Single Correct
52 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Graphical Concept
17 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Exercise 4.4
16 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE
1 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise Integer
9 Videos
Similar Questions
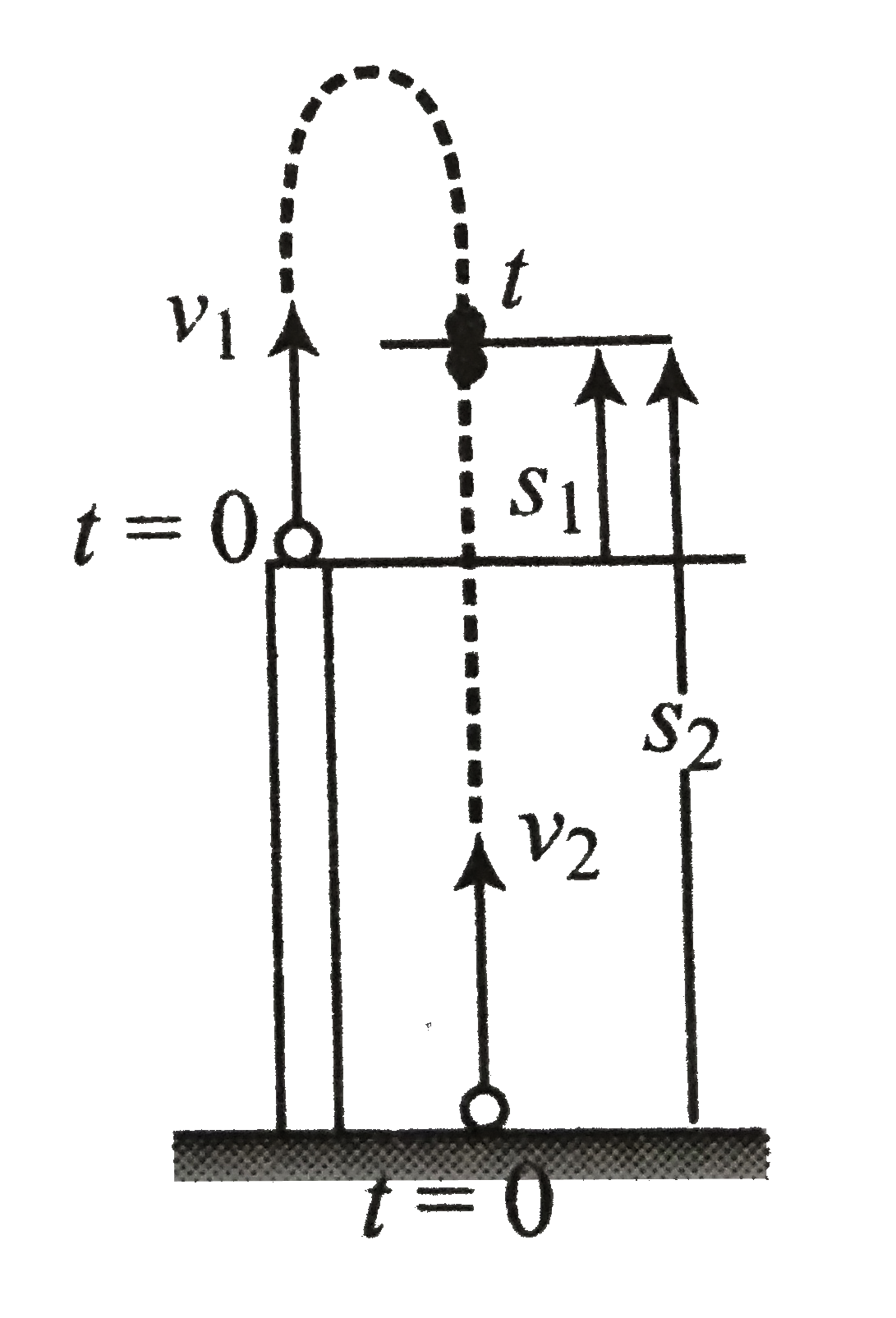
Two paarticles 1 and 2 are projected simultaneusly with velocities v1 and v2, respectively. Particle 1 is projectected vertically up from the top of a cliff of heitht h and particle 2 is projected vertically up from the bottom of the cliff. If the bodies meet (a) above the top of the cliff, (b) between the top and bottom of the the cliff, and (c ) below the bottom of the cliff, find the time of meeting of the particles.
 .
.
View SolutionTwo bodies 1 and 2 are projected simultaneously with velocities v1=2ms−1andv2=4ms−1 respectively. The body 1 is projected vertically up from the top of a cliff of height h = 10m and the body 2 is projected vertically up from the bottom of the cliff. If the bodies meet, find the time (in s) of meeting of the bodies.
View SolutionA ball is projected downward from the top of a cliff of height h with an initial speed v.Another ball is simultaneously projected vertically up from the bottommost of the cliff with the same speed.When do they meet?
View SolutionFrom the top of a cliff of height 19.6m a ball is projected horizontally. Find the time taken by the ball to reach the ground (g=9.8ms−2) .
View SolutionArrange the different parts of the root vertically, from the top to the bottom.
View SolutionA particle of mass m is projected upword with velocity v=ve2 (ve) escape of the particle is
View SolutionA stone is allowed to fall from the top of a tower 300 m height and at the same time another stone is projected vertically up from the ground with a velocity 100ms−1 . Find when and where the two stones meet ?
View SolutionA stone is dropped from the top of a tower of height h=60m. Simultaneously another stone is projected vertically upwards from the foot of the tower. They meet at a height 2h3 from the ground level. The initial velocity of the stone projected upwards is (g=10ms−2)
View SolutionFrom the top of a cliff 92 m high. the angle of depression of a buoy is 20∘ . Calculate, to the nearest metre, the distance of the buoy from the foot of the cliff
View SolutionA stone dropped from a cliff hits the ground in 4 sec. Height of the cliff is
View Solution
