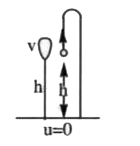
A balloon rises from rest on the ground with constant acceleration g/8. A stone is dropped from the balloon when the balloon has risen to a height of (H). Find the time taken by the stone to reach the ground.
To solve the problem, we need to find the time taken by the stone to reach the ground after it is dropped from a balloon that is rising with a constant acceleration of g8. The balloon rises to a height H before the stone is dropped.
1. Determine the velocity of the balloon when it reaches height H:
The balloon starts from rest and rises with a constant acceleration a=g8. We can use the second equation of motion:
v2=u2+2as
Here, u=0 (initial velocity), a=g8, and s=H. Thus,
v2=0+2(g8)H=gH4
Therefore, the velocity v of the balloon at height H is:
v=√gH4=√gH2
2. Set up the equation for the stone's motion:
When the stone is dropped from the balloon, it has an initial velocity v=√gH2 and it will fall under the influence of gravity. The displacement s of the stone when it reaches the ground is −H (downward direction).
We can use the second equation of motion again:
s=ut+12at2
Here, s=−H, u=√gH2, and a=g. Plugging in these values, we get:
−H=(√gH2)t+12gt2
3. Rearrange the equation:
Rearranging gives us:
12gt2+(√gH2)t+H=0
Multiplying through by 2 to eliminate the fraction:
gt2+√gHt+2H=0
4. Use the quadratic formula to solve for t:
The quadratic formula is given by:
t=−b±√b2−4ac2a
Here, a=g, b=√gH, and c=2H. Substituting these values in:
t=−√gH±√(√gH)2−4g(2H)2g
Simplifying:
t=−√gH±√gH−8gH2g=−√gH±√−7gH2g
Since we need a positive time, we discard the negative root. Thus:
t=−√gH+√7gH2g
t=(√7−1)√gH2g
5. Final result:
The time taken by the stone to reach the ground is:
t=(√7−1)√H2√g
The balloon starts from rest and rises with a constant acceleration a=g8. We can use the second equation of motion:
v2=u2+2as
Here, u=0 (initial velocity), a=g8, and s=H. Thus,
v2=0+2(g8)H=gH4
Therefore, the velocity v of the balloon at height H is:
v=√gH4=√gH2
When the stone is dropped from the balloon, it has an initial velocity v=√gH2 and it will fall under the influence of gravity. The displacement s of the stone when it reaches the ground is −H (downward direction).
s=ut+12at2
Here, s=−H, u=√gH2, and a=g. Plugging in these values, we get:
−H=(√gH2)t+12gt2
Rearranging gives us:
12gt2+(√gH2)t+H=0
Multiplying through by 2 to eliminate the fraction:
gt2+√gHt+2H=0
The quadratic formula is given by:
t=−b±√b2−4ac2a
Here, a=g, b=√gH, and c=2H. Substituting these values in:
t=−√gH±√(√gH)2−4g(2H)2g
Simplifying:
t=−√gH±√gH−8gH2g=−√gH±√−7gH2g
Since we need a positive time, we discard the negative root. Thus:
t=−√gH+√7gH2g
t=(√7−1)√gH2g
The time taken by the stone to reach the ground is:
t=(√7−1)√H2√g
Topper's Solved these Questions
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Exercise 4.3
15 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Exercise 4.4
16 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Exercise 4.1
17 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE
1 Video
- KINEMATICS-2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise Integer
9 Videos
Similar Questions
A balloon rises rest on the ground with constant acceleration 1ms−2. A stone is dropped when balloon has risen to a height of 39.2m. Find the time taken by the stone to teach the ground.
View SolutionA helicopter rises from rest on the ground vertically upwards with a constant acceleration g. A food packet is dropped from the helicopter when is at a height h. The time taken by the packet to reach the ground is close to [ g is the acceeration due to gravity] :
View Solution
Knowledge Check
A wooden ball and an iron ball are dropped from the same height h in vaccum. If their radii are the same then the time taken by then to reach the ground are
Aapproximately equalBexactly equalCnot equalDzero
A balloon starts rising from the ground with a constant acceleration of 1.25m/s2. After 8 s, a stone is released from the balloon. Find the time taken by the stone to reach the ground. (Take g=10m/s2)
View SolutionA balloon starts rising from the ground with an acceleration of 1.25 m/s2 . A stone is released from the balloon after 10s. Determine
(1) maximum height of ston from ground
(2) time taken by stone to reach the ground
View SolutionA stone is dropped from a balloon ascending with v0=2ms, from a height h=4.8 m .Find the time of flight of the stone.
View SolutionA balloon starts from rest from the ground and moves with uniform acceleration g/8. When it reaches a height h a ball is dropped from it. Find the time taken by the ball to reach the ground.
View SolutionA balloon is moving along with constant upward acceleration of 1m/s2. A stone is thrown from the balloon downwards with speed 10m/s with respect to the balloon. At the time of projectile balloon is at height 120m from the ground and is moving with speed 20m/s. Find the time required to fall on the ground by the stone after the projection.
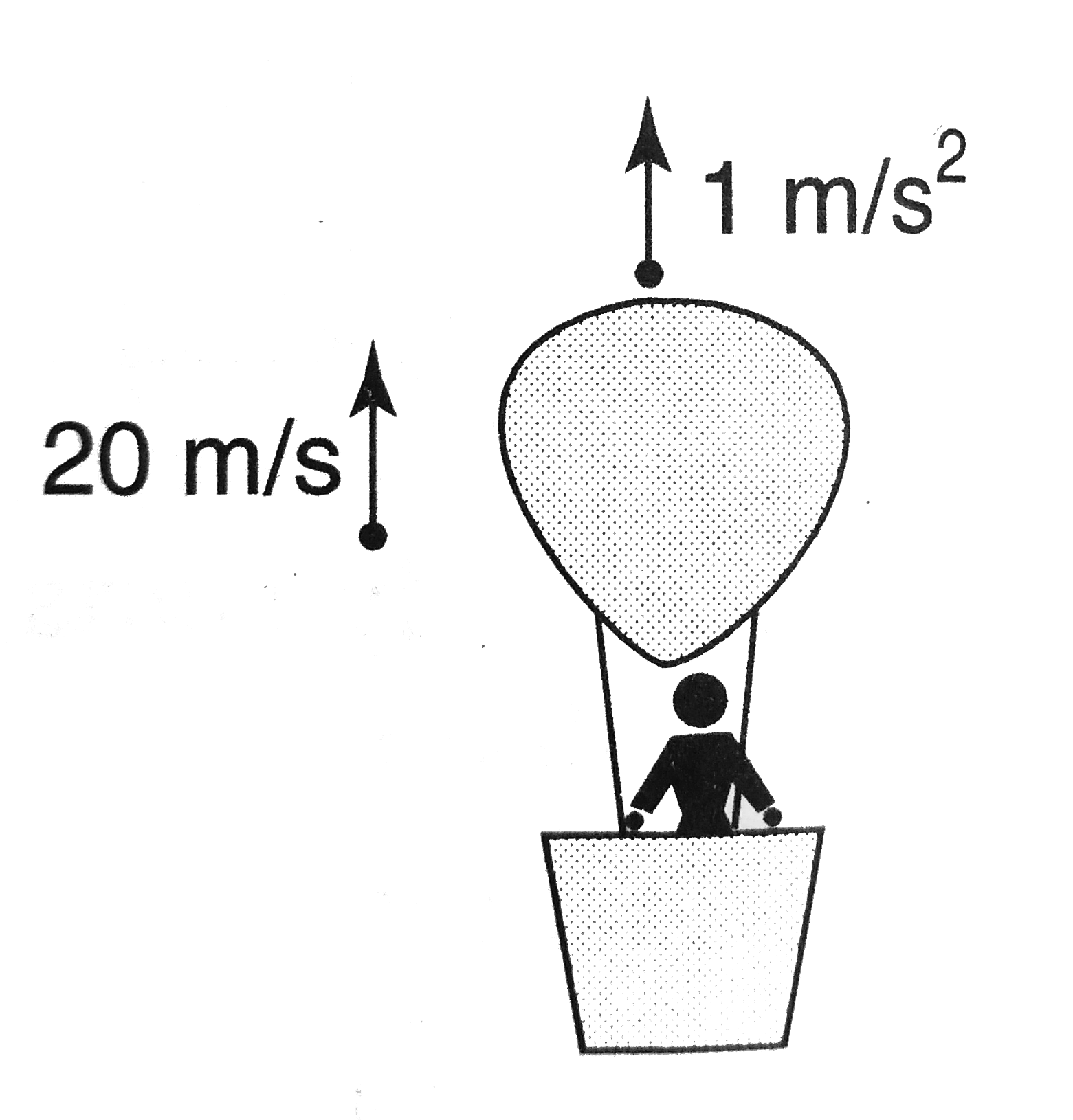
View SolutionA stone dropped from the top of a tower reaches the ground in 3 s. The height of the tower is
View SolutionA ballon starts rising from ground from rest at some constant acceleration. After some time, a storne is dropped from it. If the stone reaches the ground in the same time in which balloon reached the dropping poing from ground, find the acceleration of the balloon.
View Solution