A bar magnet suspended freely has period of oscillation of 2s. Now, the bar magnet is broken into equal halves and one-half is suspended to oscillate freely in the same magnetic field. Find the time period of oscillation of this half of the magnet.
The correct Answer is:1
To solve the problem, we need to analyze the effect of breaking the bar magnet into two halves on its moment of inertia and subsequently on its period of oscillation.
1. Understanding the Initial Conditions:
- The initial period of oscillation (T) of the bar magnet is given as 2 seconds.
- The formula for the period of oscillation of a magnet is given by:
T=2π√IM⋅B
where I is the moment of inertia, M is the mass of the magnet, and B is the magnetic field strength.
2. Moment of Inertia for the Whole Magnet:
- For a bar magnet (considered as a rod), the moment of inertia I about its end is:
I=13ML2
where L is the length of the bar magnet.
3. Breaking the Magnet into Halves:
- When the bar magnet is broken into two equal halves, each half has a mass of M/2 and a length of L/2.
- The moment of inertia I′ for one half about its end is:
I′=13(M2)(L2)2=13⋅M2⋅L24=ML224
4. Calculating the New Period of Oscillation:
- Now, substituting I′ into the period formula for the half magnet:
T′=2π√I′M′⋅B=2π
⎷ML224M2⋅B
- Simplifying this expression:
T′=2π√ML224⋅2M⋅B=2π√2L224B=2π√L212B=2π√112⋅L
5. Relating the New Period to the Old Period:
- We can relate the new period T′ to the original period T:
T′=√12T
- Since the original period T is 2 seconds:
T′=√12⋅2=√2 seconds
Final Answer:
The time period of oscillation of the half of the magnet is √2 seconds.
- The initial period of oscillation (T) of the bar magnet is given as 2 seconds.
- The formula for the period of oscillation of a magnet is given by:
T=2π√IM⋅B
where I is the moment of inertia, M is the mass of the magnet, and B is the magnetic field strength.
- For a bar magnet (considered as a rod), the moment of inertia I about its end is:
I=13ML2
where L is the length of the bar magnet.
- When the bar magnet is broken into two equal halves, each half has a mass of M/2 and a length of L/2.
- The moment of inertia I′ for one half about its end is:
I′=13(M2)(L2)2=13⋅M2⋅L24=ML224
- Now, substituting I′ into the period formula for the half magnet:
T′=2π√I′M′⋅B=2π
⎷ML224M2⋅B
- Simplifying this expression:
T′=2π√ML224⋅2M⋅B=2π√2L224B=2π√L212B=2π√112⋅L
- We can relate the new period T′ to the original period T:
T′=√12T
- Since the original period T is 2 seconds:
T′=√12⋅2=√2 seconds
The time period of oscillation of the half of the magnet is √2 seconds.
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - MAGNETIC FORCEEXERCISE - Practice Questions (Matrix - Match)2videos
MAGNETIC FORCE
- BOOK - RESNICK AND HALLIDAYCHAPTER - MAGNETIC FIELDS DUE TO CURRENTSEXERCISE - Practice Question (Integer Type)4videos
MAGNETIC FIELDS DUE TO CURRENTS
- BOOK - RESNICK AND HALLIDAYCHAPTER - MOTION ALONG A STRAIGHT LINEEXERCISE - PRACTICE QUESTIONS ( Integer Type )3videos
MOTION ALONG A STRAIGHT LINE
Similar Questions
An object suspended from a spring exhibits oscillations of period T. Now ,the spring is cut in half and the two halves are used to support the same object, as shown in figure. Show that the new period of oscillation is T/2.
 .View Solution
.View SolutionA thin rectangular magnet suspended freely has a period of oscillation T in a uniform magnetic field . Now it is broken in two equal parts perpendicular to magnetic axis and one place is allowed to oscillate in the same field . If its period of oscillation is T' , then ration TT' is
View Solution
Knowledge Check
- Question 1 - Select One
A thin rectangular magnet suspended freely has a period of oscillation equal to T. Now it is broken into two equal halves (each having half of the original length) and one piece is made to oscillate freely in the same field. If its period of oscillation is T′, then ratio T′T is
A14B12√2C12D2 - Question 2 - Select One
A thin rectangular magnet suspended freely has a period of oscillation equal to T . Now it is broken into two equal halves (each having half of the original length)ando≠πeceismade→oscillateeely∈thesamefield.Ifitsperiodofmade→oscillateeely∈thesamefield.ifitsperiodofoscillationis'T',theratio(T')/(T) is
A12√2B12C2D14 - Question 3 - Select One
Time period of oscillation of a magnetic needle is
AT=√TMBBT=2π√IMBCT=2π√MBIDT=π√MBI
A thin rectangular magnet suspnded freely has a period of oscillation of 4s . If it is broken into one of the pieces is suspened similarly . The period of its oscillation will be
View SolutionAn object suspended from a spring exhibits oscillations of period T. Now the spring is cut in two halves and the same object is suspended with two halves as shown in figure. The new time period of oscillation will become
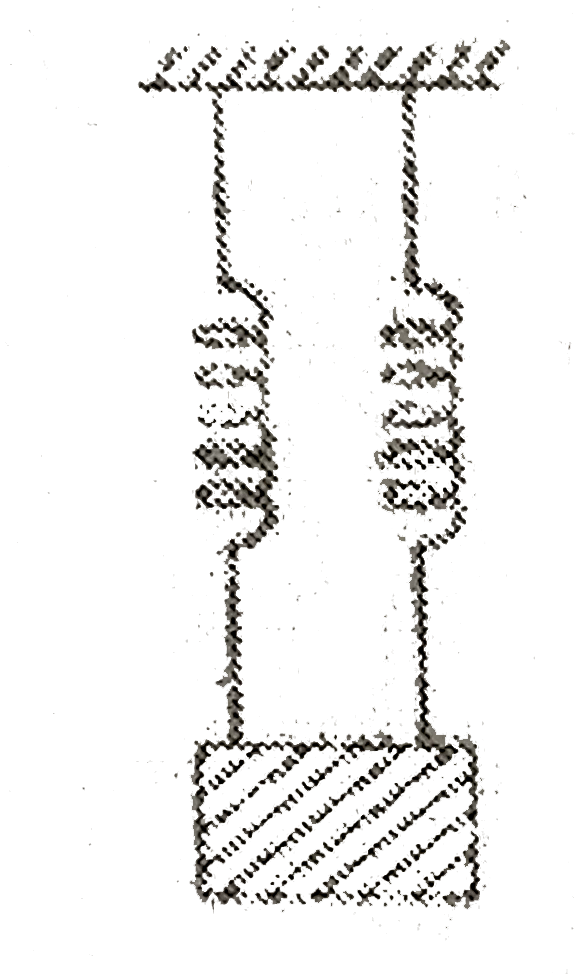 View Solution
View SolutionA magnet, when suspended in an external magnetic field, has a period of oscillation of 4 s. When it is cut length wise, and suspended in the same magnetic field, the period of vibration will be
View SolutionA spring has a certain mass suspended from it and its period for vertical oscillation is T. The spring is now cut into two equal halves and the same mass is suspended from one of the halves. The period of vertical oscillation is now
View SolutionThe time period of a mass suspended from a spring is T if the spring is cut in to equal part and the same mass is suspended from one of the part then the time period will be
View Solution

