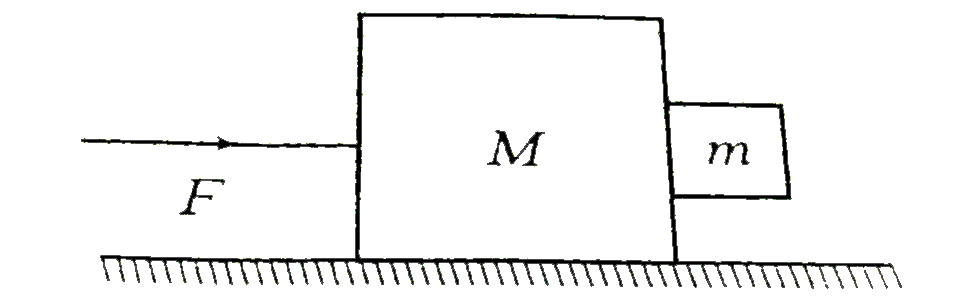
A bar of mass $m$ is placed on a triangular block of mass $M$ as shown in figure The friction coefficient between the two surface is $μ$ and ground is smooth find the minimum and maximum horizontal force $F$ required to be applied on block so that the bar will not slip on the inclined surface of block

Video Solution

Text Solution

Verified by Experts

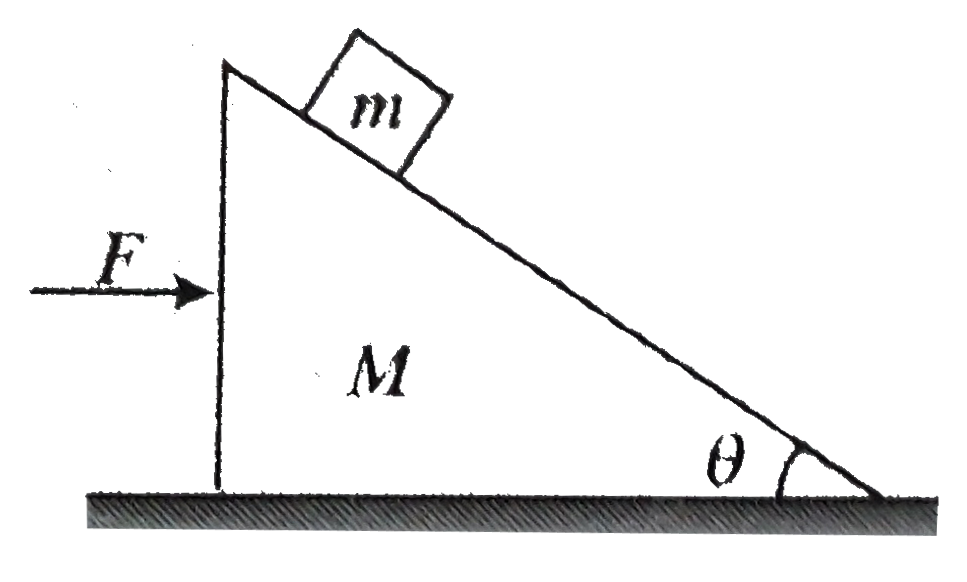
Here if both the masses are moving together , accceleration of the system will be $a = F 1 (M + m)$ .If we observe the mass $m$ relation to $M$ . It experience a pseudo force out $m a$ toward left . Along the incline it experience two forces $m g sin θ$ downwards and $m a cos θ$ upward . If $m g sin θ$ is morethen $m a cos θ$ will act in upward direction here if block $m$ is in equlibrium on inclined surface , we most have

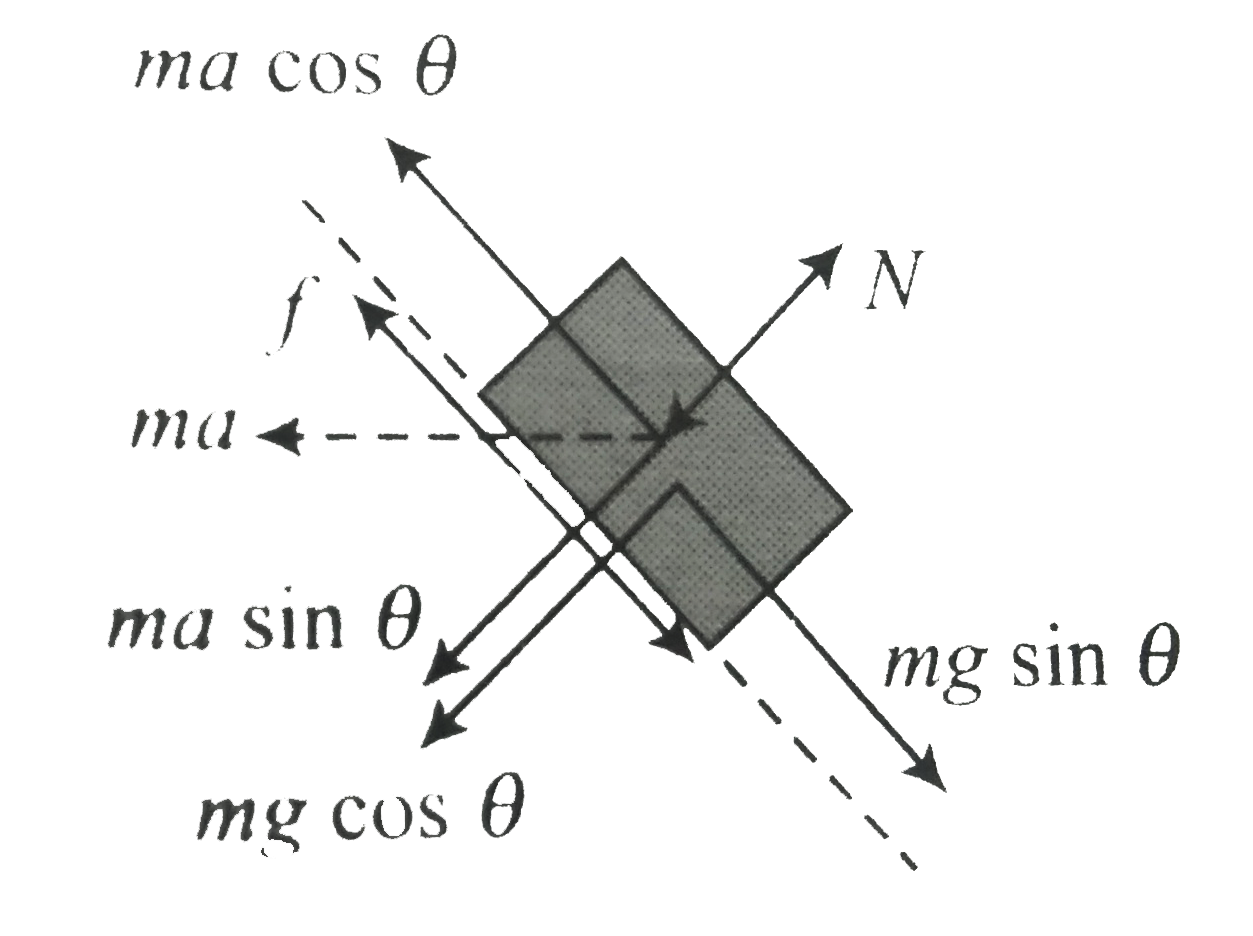
$f = μ N$ ,
Here $f = (m g sin θ - m a cos θ)$
and $N = (m a sin θ + m g cos θ)$
$f = m g sin θ - m a cos θ \leq μ (m g cos θ + m a sin θ)$
or $a \geq \frac{sin θ - μ cos θ}{cos θ + μ sin θ} g$
or $(M + m) a \geq \frac{sin θ - μ cos θ}{cos θ + μ sin θ} (M + m) g$
$F \geq \frac{sin θ - μ cos θ}{cos θ + μ sin θ} (M + m) g$ ....(i)
If force is more than the value obtaional in Eq (i) $m a cos θ$ will increase on $m$ and the static friction on it will derection At $a = g tan θ$ (when $F = (M + m) g tan θ)$ we know that the force $m g sin θ$ will be balanced by $m a cos θ$ at this acceleration no friction will act on it , if applied force will increase belond values , $m a cos θ$ will execed $m g sin θ$ and friction static in downward direction here if block $m$ is in equation we must have $f = (m a cos θ - m g sin θ) N = (m g cos θ + m a sin θ)$ and $f \leq μ N$

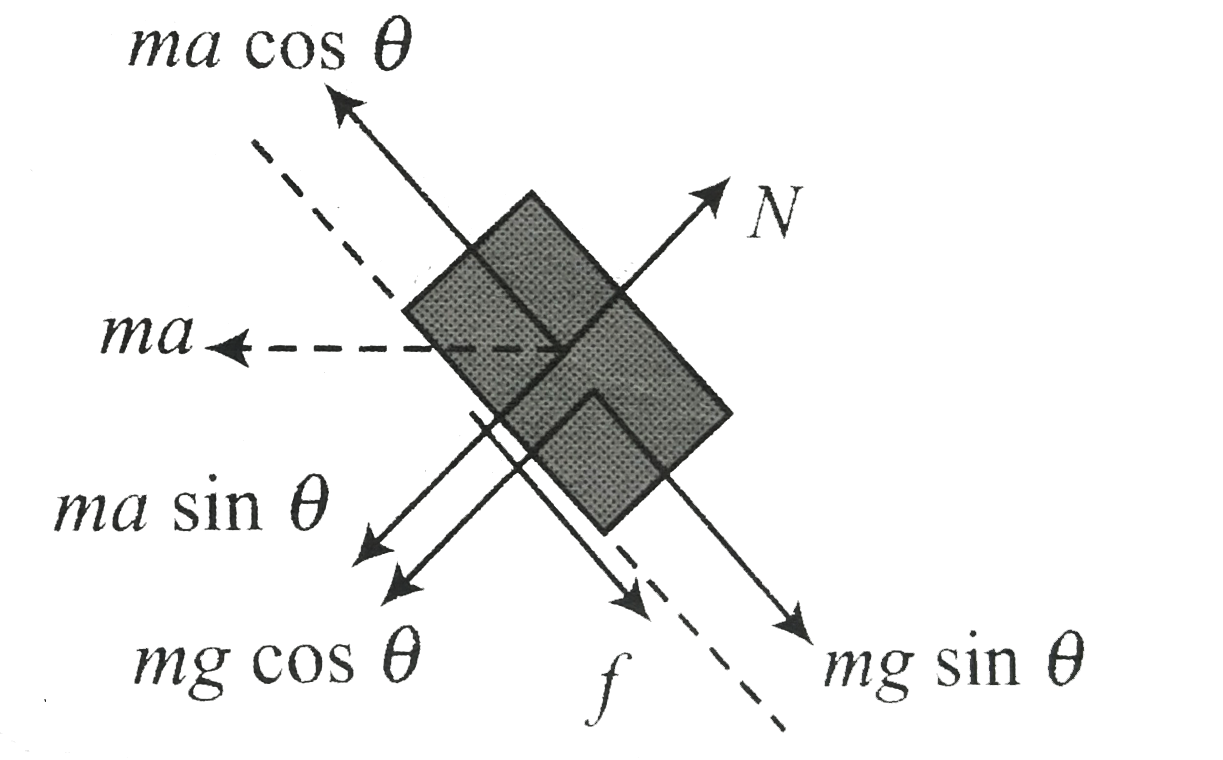
$m a cos θ - m g sin θ \leq μ (m g cos θ + m a sin θ)$
$\Rightarrow a \leq \frac{sin θ + μ cos θ}{cos θ - μ sin θ} g$
$\Rightarrow (M + m) a \leq \frac{sin θ + μ cos θ}{cos θ - μ sin θ} (M + m) g$
$\Rightarrow F \leq \frac{sin θ + μ cos θ}{cos θ - μ sin θ} (M + m) g$
Hence $F_{min} \leq \frac{sin θ - μ cos θ}{cos θ + μ sin θ} (M + m) g$
and $F_{max} \leq \frac{sin θ + μ cos θ}{cos θ - μ sin θ} (M + m) g$

Updated on:21/07/2023