A bar of mass m is pulled by means of a thread up an inclined plane forming an angle θ with the horizontal as shown in figure-2.211. The coefficient of friction is μ. Prove that
(a)α=tan−1μ, where α is the angle which the thread must from with the inclined plane for the tension of the thread to be minimum.
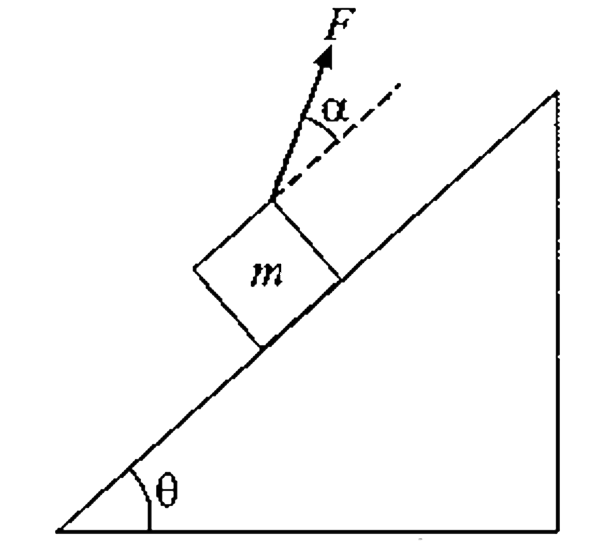
The correct Answer is:Tmin=mgsinθ+μmgcosθ√1+μ2
Step by step video, text & image solution for A bar of mass m is pulled by means of a thread up an inclined plane forming an angle theta with the horizontal as shown in figure-2.211. The coefficient of friction is mu. Prove that (a)alpha=tan^(-1)mu, where alpha is the angle which the thread must from with the inclined plane for the tension of the thread to be minimum. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- NEWTONS LAWS OF MOTIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Advance MCQs
17 Videos
- LINEAR MOMENTUM & ITS CONSERVATIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - LINEAR MOMENTUM & ITS CONSERVATIONEXERCISE - exercise 1.3
3 Videos
- RIGID BODIES AND ROTATIONAL MOTIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - RIGID BODIES AND ROTATIONAL MOTIONEXERCISE - Unsolved Numerical
63 Videos
Similar Questions
A bar of mass m is pulled by means of a thread up an inclined plane forming an angle α with the horizontal (figure). The coefficient of friction is equal to k. Find the angle β which is thread must form with the inclined plane for the tension of the thread to be minimum. What is it equal to?

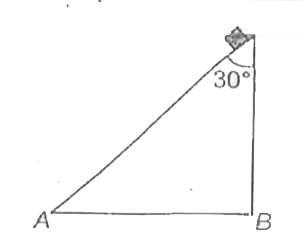
View SolutionA body of mass M starts sliding down on the inclined plane where the critical angle is ∠ACB=30∘ as shown in figure. The coefficient of kinetic friction will be
View Solution
Knowledge Check
An inclined plane is inclined at an angle θ with the horizontal. A body of mass m rests on it, if the coefficient of friction is μ, then the minimum force that has to be applied to the inclined plane to make the body just move up the inclined plane is
AmgsinθBμmgcosθCμmgcosθ−mgsinθDμmgcosθ+mgsinθA body of mass M starts sliding down an Inclined plane where critical angle is <ACB=30∘ as shown in figure, the coefficient of friction will be
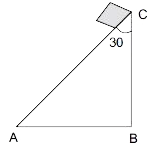 AMg√3B√3MgC√3DNone of these
AMg√3B√3MgC√3DNone of theseA block of mass m is placed on a rough plane inclined at an angle θ with the horizontal. The coefficient of friction between the block and inclined plane is μ . Ifθ<tan−1(μ) , then net contact force exerted by the plane on the block is :
Amg cos θBmgCmg sin θDNone of these
A body with zero initial velocity slips from the top of an inclined plane forming an angle α with the horizontal. The coefficient of friction μ between the body and the plane increases with the distance s from the top according to the law μ=bs. After what distance the body will stop.
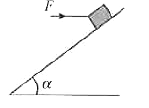
View SolutionA block of mass m in the equilib rium on a rough inclined plane with inclination α and coefficient of friction as shown in the figure (μ<tanα). A force F is applied on the block which makes an angle θ with the horizontal as shown in diagram.
View SolutionA block of mass m slides down an inclined plane which makes an angle θ with the horizontal. The coefficient of friction between the block and the plane is μ. The force exerted by the block on the plane is
View SolutionA body of mass 10 kg is lying on a rough plane inclined at an angle of 30∘ to the horizontal and the coefficient of friction is 0.5. the minimum force required to pull the body up the plane is
View SolutionA block of mass m slides down a rough inclined plane of inclination θ with horizontal with zero initial velocity. The coefficient of friction between the block and the plane is μ with θ>tan−1(μ). Rate of work done by the force of friction at time t is
View Solution
