A batsman deflects a ball by an angle of 45∘ without changing its initial speed which is equal to 54kmh. What is the impulse imparted to the ball ? (Mass of the ball is 0.15 kg)
To solve the problem of calculating the impulse imparted to a ball deflected by a batsman at an angle of 45 degrees without changing its initial speed, we can follow these steps:
1. Identify Given Data:
- Initial speed of the ball, U=54km/h
- Mass of the ball, m=0.15kg
- Deflection angle, θ=45∘
2. Convert Speed to Meters per Second:
To convert the speed from kilometers per hour to meters per second, we use the conversion factor:
1km/h=518m/s
Therefore,
U=54×518=15m/s
3. Determine the Components of Velocity:
When the ball is deflected at an angle of 45∘, the final velocity components can be calculated. The initial velocity components are:
- Horizontal component: Ux=Ucos(0∘)=U
- Vertical component: Uy=Usin(0∘)=0
After deflection, the components become:
- New horizontal component: Vx=Ucos(45∘)=U√2
- New vertical component: Vy=Usin(45∘)=U√2
4. Calculate Change in Momentum:
The impulse imparted to the ball is equal to the change in momentum. The change in momentum can be calculated as:
Δp=m(V−U)
Since the horizontal component remains unchanged and only the vertical component changes direction, we focus on the vertical component:
- Initial vertical momentum: pinitial=0
- Final vertical momentum: pfinal=m⋅Vy=m⋅U√2
Thus, the change in momentum is:
Δp=m(U√2−0)+m(0−(−U√2))=2mU√2
5. Substituting Values:
Now substituting the known values into the equation:
Δp=2⋅0.15⋅15√2=0.3⋅15√2=4.5√2≈3.18kg m/s
6. Final Impulse Calculation:
The impulse imparted to the ball is:
J=Δp≈3.18kg m/s
Final Answer:
The impulse imparted to the ball is approximately 3.18 kg m/s.
- Initial speed of the ball, U=54km/h
- Mass of the ball, m=0.15kg
- Deflection angle, θ=45∘
To convert the speed from kilometers per hour to meters per second, we use the conversion factor:
1km/h=518m/s
Therefore,
U=54×518=15m/s
When the ball is deflected at an angle of 45∘, the final velocity components can be calculated. The initial velocity components are:
- Horizontal component: Ux=Ucos(0∘)=U
- Vertical component: Uy=Usin(0∘)=0
- New horizontal component: Vx=Ucos(45∘)=U√2
- New vertical component: Vy=Usin(45∘)=U√2
The impulse imparted to the ball is equal to the change in momentum. The change in momentum can be calculated as:
Δp=m(V−U)
Since the horizontal component remains unchanged and only the vertical component changes direction, we focus on the vertical component:
- Initial vertical momentum: pinitial=0
- Final vertical momentum: pfinal=m⋅Vy=m⋅U√2
Δp=m(U√2−0)+m(0−(−U√2))=2mU√2
Now substituting the known values into the equation:
Δp=2⋅0.15⋅15√2=0.3⋅15√2=4.5√2≈3.18kg m/s
The impulse imparted to the ball is:
J=Δp≈3.18kg m/s
The impulse imparted to the ball is approximately 3.18 kg m/s.
Topper's Solved these Questions
Similar Questions
A batsman deflects a ball by an angle of 45∘ without changing its initial speed which is equal to 54kmh . What is the impulse imparted to the ball ? ( Mass of the ball is 0.15 kg)
View SolutionA batsman deflects a ball by an angle of 45∘ without changing its initial speed which is equal to 54kmh . What is the impulse imparted to the ball ? ( Mass of the ball is 0.15 kg)
View Solution
Knowledge Check
A batsman hits back a ball of mass 0.2 kg, straight in the direction of the bowler without chaning its initial speed of 6 m/s. What is the impulse impated to the ball?
A1.6N-sB2.4N-sC3.2N-sD4 N-sA ball of mass m strikes a rigid walJ with speed u and rebounds with the same speed. The impulse imparted to the ball by the wall is
A2muBmuCzeroD−2muA ball of mass m strikes a rigid walJ with speed u and rebounds with the same speed. The impulse imparted to the ball by the wall is
 Amu sin30∘tB2mu sin30∘tCmu cos30∘tD2mu cos30∘t
Amu sin30∘tB2mu sin30∘tCmu cos30∘tD2mu cos30∘t
A batsman deflects a ball by an angle of 90∘ without changing its initial speed, which is equal to 54 km/hr. What is the impulse to the ball ? Mass of the ball is 0.15 kg.
View SolutionA batsman hits back a ball straight in the direction of the bowler without changing its initial speed of 15m/s.If the mass of ball is 0.1kg then impulse imparted to the ball will be
View SolutionA batsman hits back a ball straight in the direction of the bowler without changing its initial speed of 12ms−1 . If the mass of the ball is 0.15 kg , determine the impulse imparted to the ball . (Assume linear motion of the ball).
View SolutionA player kicks a ball at an angle of 37∘ to the horizontal with an initial speed of 15ms−1 . Find its time of fight.
View SolutionA particle of mass m strikes a wall with speed v at an angle 30∘ with the wall elastically as shown in the figure. The magnitude of impulse imparted to the ball by the wall is
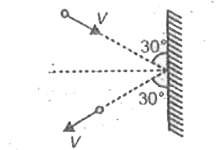
View Solution
