A battery is formed by connecting three cells in series .
The emfs of cells are 5 V, 2.5 V and 1.5 V and their internal resistance are 0.5Ω,0.05Ωand0.45Ω respectively.
This battery is connected across a load resistance of 5Ω what current will be supplied by the battery ? if the cell of emf 1.5 V were connected with reverse polarity then what would have been the current supplied by the battery ?
To solve the problem step by step, we will first calculate the total EMF and total internal resistance of the battery formed by the three cells connected in series. Then, we will find the current supplied by the battery when connected to a load resistance of 5 ohms. Finally, we will analyze the scenario where the cell with 1.5 V is connected with reverse polarity.
Step 1: Calculate the Total EMF of the Battery
The total EMF (E) of the battery formed by connecting the three cells in series is the sum of the individual EMFs of the cells.
E=E1+E2+E3
Where:
- E1=5V
- E2=2.5V
- E3=1.5V
Calculating the total EMF:
E=5+2.5+1.5=9V
Step 2: Calculate the Total Internal Resistance
The total internal resistance (R_internal) of the battery is the sum of the internal resistances of the individual cells.
Rinternal=r1+r2+r3
Where:
- r1=0.5Ω
- r2=0.05Ω
- r3=0.45Ω
Calculating the total internal resistance:
Rinternal=0.5+0.05+0.45=1Ω
Step 3: Calculate the Total Resistance in the Circuit
The total resistance (R_total) in the circuit is the sum of the load resistance (R_load) and the total internal resistance.
Rtotal=Rinternal+Rload
Where:
- Rload=5Ω
Calculating the total resistance:
Rtotal=1+5=6Ω
Step 4: Calculate the Current Supplied by the Battery
Using Ohm's law, the current (I) supplied by the battery can be calculated as:
I=ERtotal
Substituting the values:
I=9V6Ω=1.5A
Step 5: Analyze the Case with Reverse Polarity
If the cell with 1.5 V is connected with reverse polarity, the effective EMF will decrease by the value of that cell.
E′=E1+E2−E3
Calculating the new EMF:
E′=5+2.5−1.5=6V
The total internal resistance remains the same at 1 Ω, and the load resistance is still 5 Ω. Thus, the total resistance remains 6 Ω.
Step 6: Calculate the New Current
Using Ohm's law again for the new scenario:
I′=E′Rtotal
Substituting the new EMF:
I′=6V6Ω=1A
Final Answers:
1. The current supplied by the battery when all cells are connected normally is 1.5 A.
2. The current supplied by the battery when the 1.5 V cell is connected with reverse polarity is 1 A.
The total EMF (E) of the battery formed by connecting the three cells in series is the sum of the individual EMFs of the cells.
Where:
- E1=5V
- E2=2.5V
- E3=1.5V
E=5+2.5+1.5=9V
The total internal resistance (R_internal) of the battery is the sum of the internal resistances of the individual cells.
Where:
- r1=0.5Ω
- r2=0.05Ω
- r3=0.45Ω
Rinternal=0.5+0.05+0.45=1Ω
The total resistance (R_total) in the circuit is the sum of the load resistance (R_load) and the total internal resistance.
Where:
- Rload=5Ω
Rtotal=1+5=6Ω
Using Ohm's law, the current (I) supplied by the battery can be calculated as:
I=9V6Ω=1.5A
If the cell with 1.5 V is connected with reverse polarity, the effective EMF will decrease by the value of that cell.
Calculating the new EMF:
E′=5+2.5−1.5=6V
Using Ohm's law again for the new scenario:
I′=6V6Ω=1A
1. The current supplied by the battery when all cells are connected normally is 1.5 A.
2. The current supplied by the battery when the 1.5 V cell is connected with reverse polarity is 1 A.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - PRACTICE PROBLEMS
71 Videos
- CURRENT ELECTRICITYBOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - CONCEPTUAL QUESTIONS
35 Videos
- ATOMS BOOK - MODERN PUBLICATIONCHAPTER - ATOMS EXERCISE - Chapter Practice Test
16 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - MODERN PUBLICATIONCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - CHAPTER PRACTICE TEST
15 Videos
Similar Questions
Three cells of emf 2.0 v, 1.8 V and 1.5 V are connected in series. Their internal resistances are 0.05Ω,0.7Ω and 1Ω respectively. If the battery is connected to an external resistor of 4Ω via a very resistance ammeter, what would be the reading in the ammeter ?
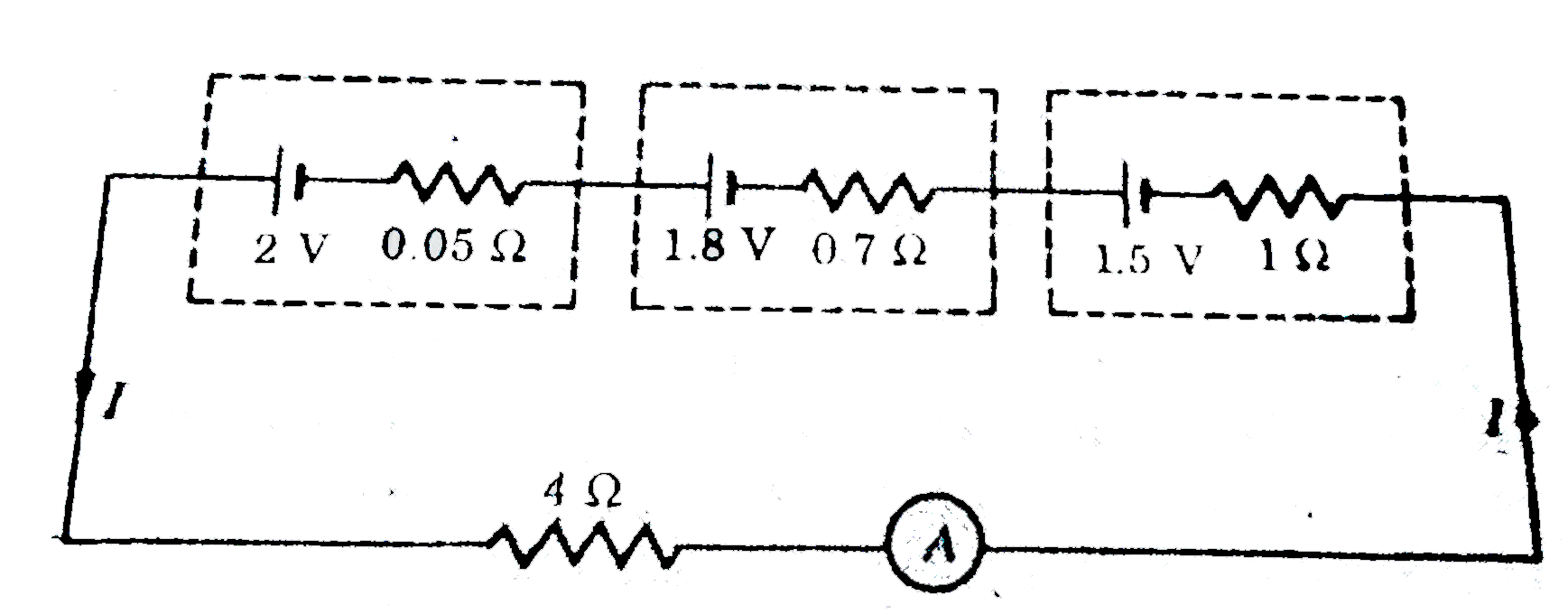
View SolutionTwo cells of emfs 1.5 V and 2.0v having internal resistance 0.2Σ and 0.3 Σ respectively are connected in parallel . Calculate the emf and internal resistance of the equivalent cell .
View Solution
Knowledge Check
Two batteries of emfs 2 V and 1 V of internal resistances 1Ωand2Ω respectively are connected in parallel. The effective emf of the combination is
A32VB53VC35VD2V
Two cells connected in series have electromotive force of 1.5 V each. Their internal resistances are 0.5Ω and 0.25Ω respectively. This combination is connected to a resistance of 2.25Ω. Calculate the current flowing in the circuit and the potential differnce across the terminals of each cell.
View SolutionTwo cells of emfs 1.5 V and 2.0 V having internal resistances 0.2Ω and 0.3Ω respectively are connected in parallel. Calculate the emf and internal resistance of the equivalent cell.
View SolutionA 3-V battery is connected across a 5−Ω resistance. Calculate the heat produced in 5 seconds.
View SolutionIn the circuit, the cells E1andE2 have emfs of 4V and 8V and internal resistance 0.5Ωand1.0Ω, respectively. Calculate the current through 6Ω resistance.
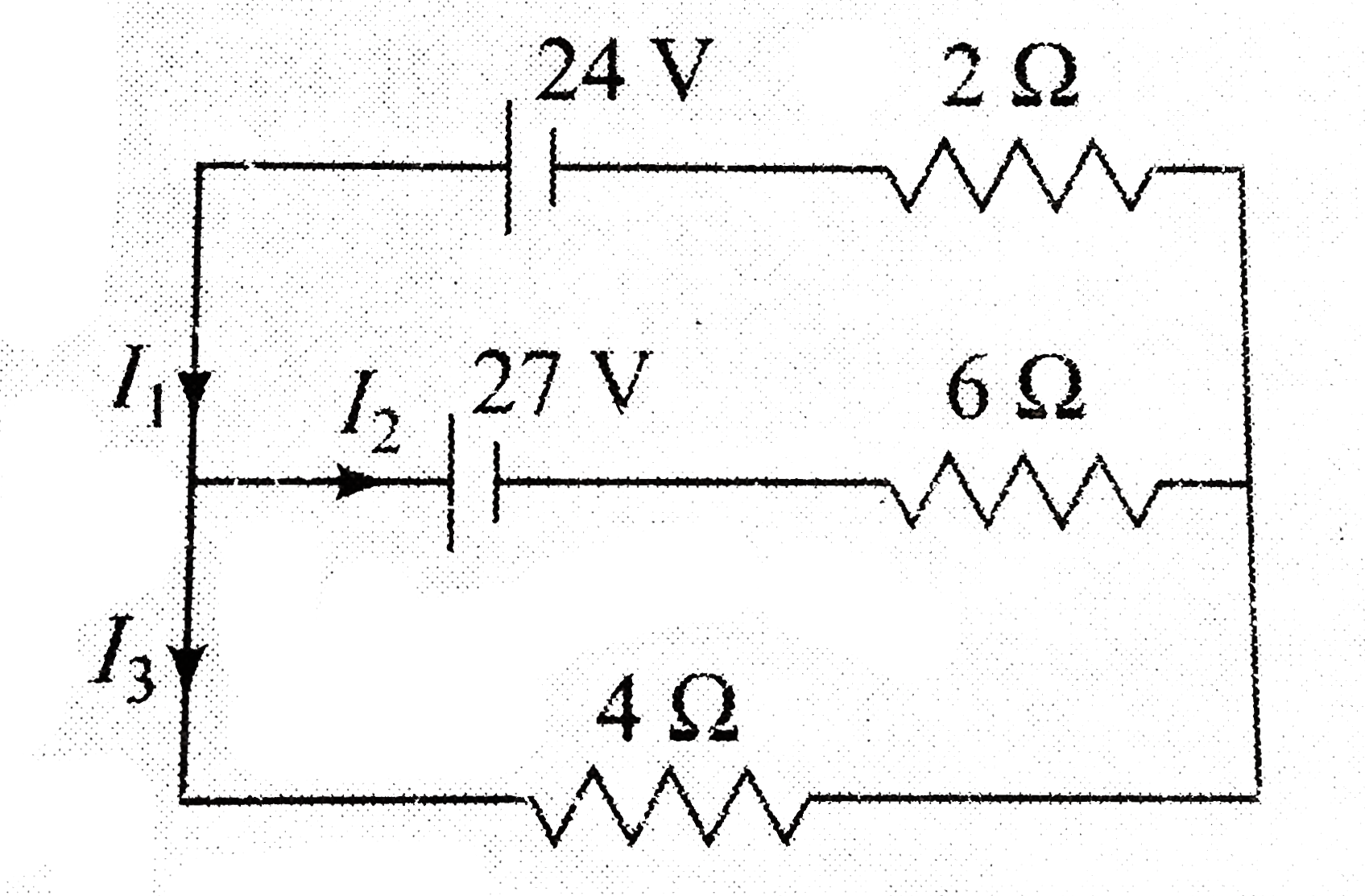
View Solution(a) Three cells of emfs, 1.5 V, 2.0V and 2.5 V are connected in series. Their internal resistance are 0.20Ω,0.15Ω and 0.15Ω respectively. The battery is connected to an external resistor of 5.5Ω via a very low resistance ammeter, what would be the reading of ammeter?
(b) If the three cells above were joined in parallel, would they be characterised by a definite emf and internal resistance (independent of their individual internal resistance )? If not, how will you obtain currents in different branches of the circuit ?
View SolutionIn the circuit shown in Fig. 4.68, the cells ε1 and ε2 have emf's of 4 V and 8 V and internal resistances of 0.5Ω and 1Ω respectively. Calculate the current in each resistance.
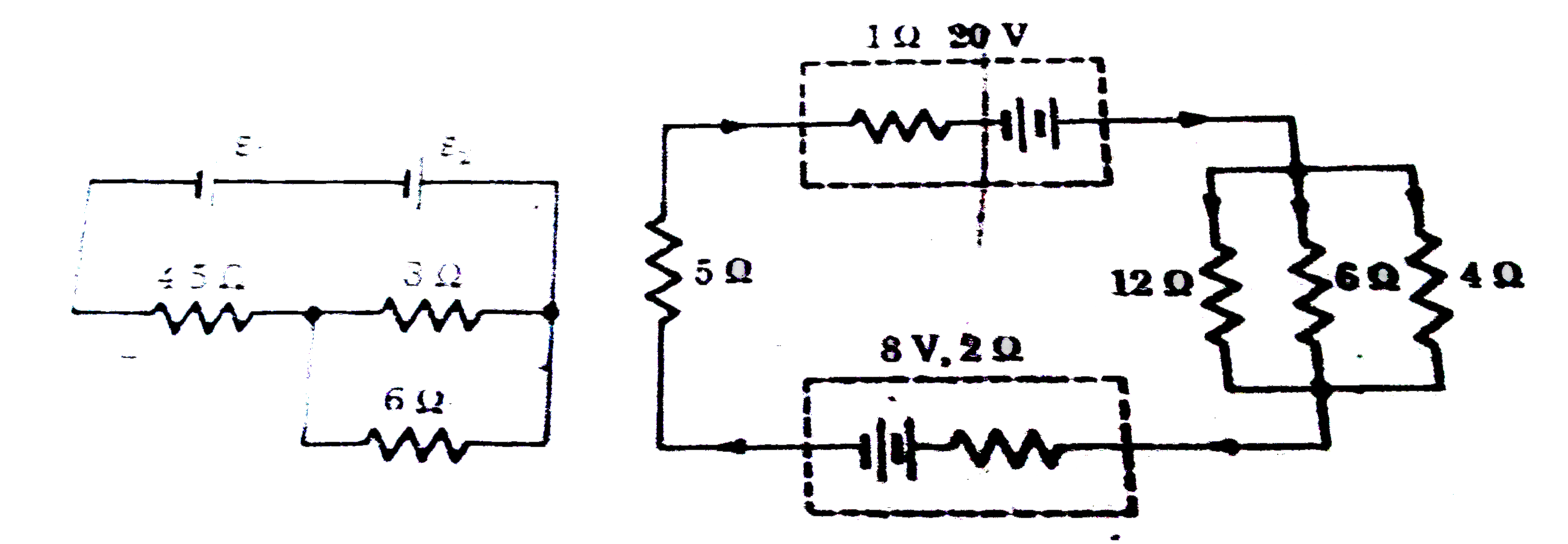
View SolutionTwo cells of 1.5 V and 2 V , having internal resistances of 1Ω and 2Ω respectively, are connected in parallel so as to read the current in the same direction through an external resistance of 5Ω . The current in the external resistance will be
View Solution
