A bead of mass m stays at point P (a,b) on a wire bent in the shape of a parabola y=4Cx2 and rotating with angular speed ω (see figure ) . The value of ω is (neglect friction),
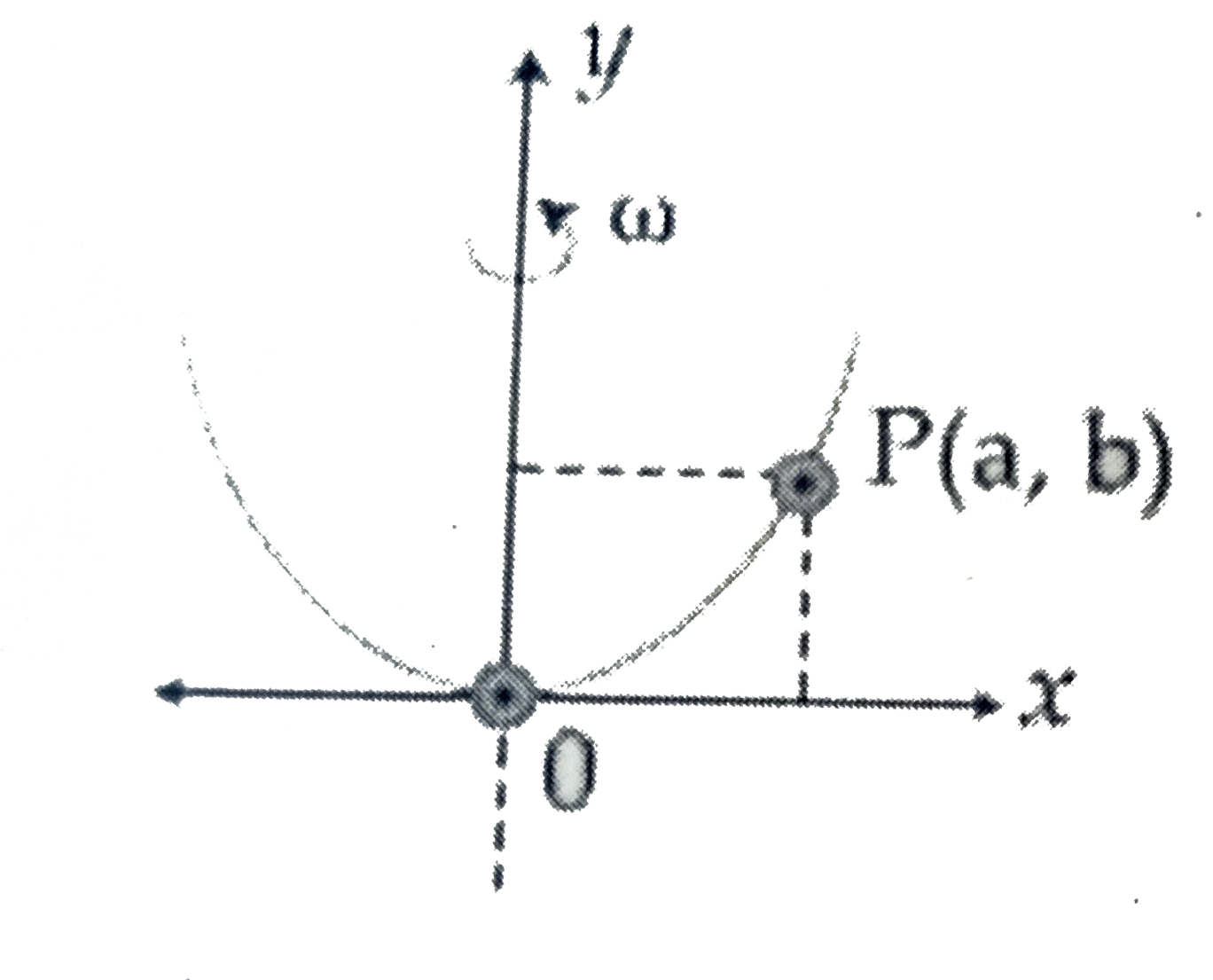
2√gC
2√2gC
√2gCab
√2gC
Step by step video & image solution for A bead of mass m stays at point P (a,b) on a wire bent in the shape of a parabola y =4 Cx^(2) and rotating with angular speed omega (see figure ) . The value of omega is (neglect friction), by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A disc of mass m and radius R rotating with angular speed ω0 is placed on a rough surface (co-officient of friction =μ). Then

View SolutionA bead of mass m can move without friction along a long wire bent in a vertical plane in the shape of a graph of a certain function. Let lA be the length of the segment of the wire from the origin to a certain point A. It is knonw that if the bead is released at point A such that lA<lA0, its motion will be strictly harmonic l(t)=lAcosωt. Prove that there exists a point B(lA0<<lB) at which the condition of harmonicity of oscillations will be violated.
View Solution
Knowledge Check
A thin circular ring of mass per unit length p and radius r is rotating at an angular speed ω as shown in figure. The tension in the ring is
 Apω2r2/2Bpω2r2Cpω2r2/3DNone
Apω2r2/2Bpω2r2Cpω2r2/3DNoneA smooth wire frasme is in the shape of a parabola y=5x2 . It is being rotated about y-axis with an angular velocity ω. A small bead of mass (m=1kg) is at point P and is in equilibrium with respect to the frame. Then the angular velocity ω is (g=10m/s2)
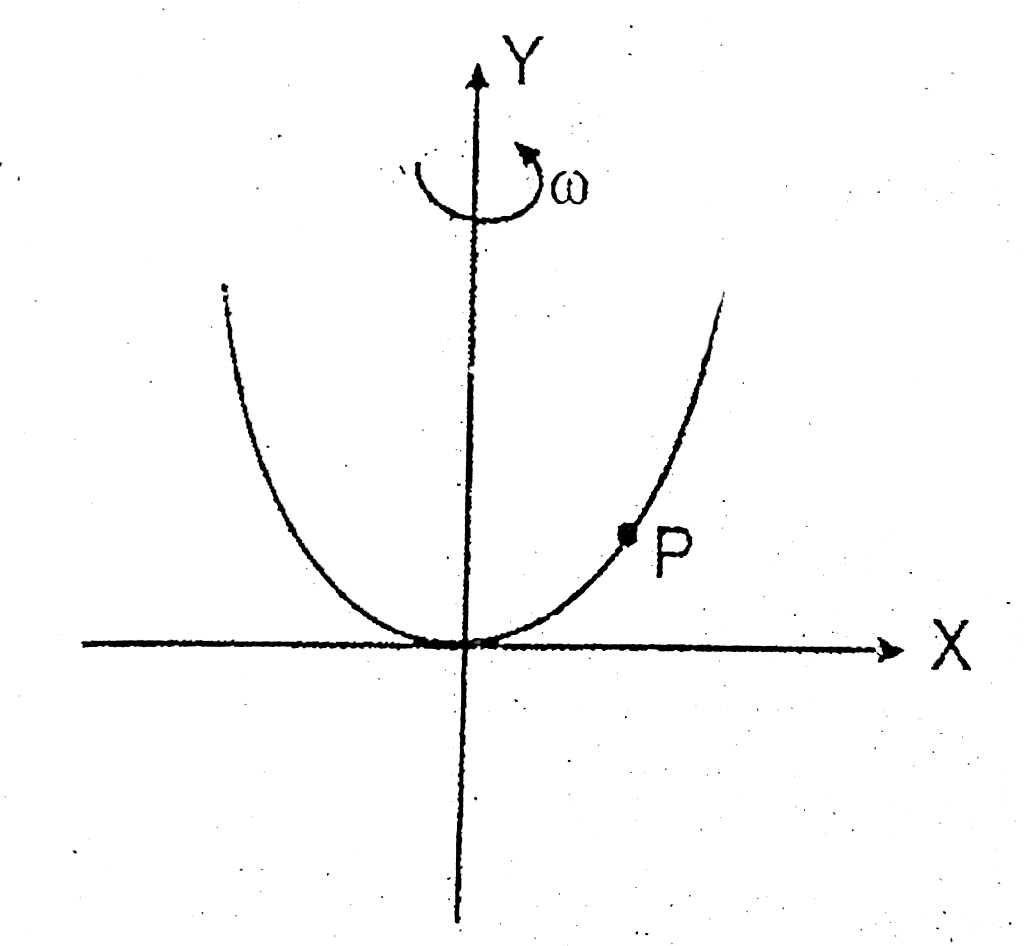 Aω=5rad/secBω=10rad/secCω=20rad/secDDepends of x-coordinate of particle
Aω=5rad/secBω=10rad/secCω=20rad/secDDepends of x-coordinate of particleA piece of wire is bent in the shape of a parabola y=Kx2 (y - axis vorical) with a bead of mass m on it . The beat can side on the wire without friction , it stays the wire is now accleated parallel to the bead , where the bead can stay at rest with repect to the wire from the y - axis is
AagkBa2gkC2agkDa4gk
A body Is placed on a turntable. The friction coefficient between the body and the table is μ.
(a) If turntable rotates at constant angular speed ω, find the maximum value of ω for which the block will not slip.
(b) if the angular speed is increased uniformly from rest with an angular acceleration α, at what speed will the block slip?

View SolutionA steel wire of negligible mass length L0 and cross sectional area A0 is kept on a smooth horizontal table with one end fixed. A ball of mass M is attached to the other end. The wire and ball are rotating with angular velocity ω . If elongation in the wire is ΔL, then the value of Young's modulus of elasticity will be
View SolutionA piece of wire is bent in the shape of a parabola y=kx2 (y-axis vertical) with a bead of mass m on it. The bead can slide on the wire without friction. It stays at the lowest point of the parabola when the wire is at rest. The wire is now accelerated parallel to the x-axis with a constant acceleration a. The distance of the new equilibrium position of the bead, where the bead can stay at rest with respect to the wire, from the y-axis is:
View SolutionA small ring P is threaded on a smooth wire bent in the form of a circle of radius a and centre O. The wire is rotating with constant angular speed ω about a vertical diameter xy, while the ring remains at rest relative to the wire at a distance a2 from xy. Then is equal to:
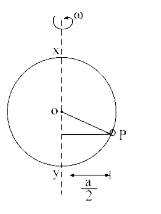
View SolutionA rod of mass m and length l is rotating about a fixed point in the ceiling with an angular velocity ω as shown in the figure. The rod maintains a constant angle θ with the vertical.
What will be the horizontal component of angular momentum of the rod about the point of suspension in terms of m, ω, l and θ.

View Solution
