Doubtnut Promotions Sticky

If the maximum value of accelerating potential provided by a radio frequency oscillator is 12 kV. The number of revolution made by a proton in a cyclotron to achieve one sixth of the speed of light is _______

Video Solution
Doubtnut Promotions Banner
Text Solution
Generated By DoubtnutGPT

To solve the problem, we need to determine the number of revolutions made by a proton in a cyclotron to achieve one sixth of the speed of light (v = c/6) when the maximum accelerating potential is 12 kV.

1. Identify Given Values:
- Maximum accelerating potential (V) = 12 kV = 12 × 10^3 V
- Speed of light (c) = 3 × 10^8 m/s
- Desired speed of proton (v) = c/6 = (3 × 10^8 m/s) / 6 = 5 × 10^7 m/s

2. Calculate Kinetic Energy of Proton:
The kinetic energy (KE) of the proton when it reaches the speed v is given by:
KE=12mv2
where m is the mass of the proton (approximately 1.67×10−27 kg).
KE=12×1.67×10−27×(5×107)2
KE=12×1.67×10−27×2.5×1015=2.0875×10−12 J

3. Calculate Energy Gained from the Electric Field:
The energy gained by the proton in one revolution due to the potential difference is given by:
Energy gained per revolution=qV
where q is the charge of the proton (approximately 1.6×10−19 C).
Energy gained per revolution=(1.6×10−19 C)×(12×103 V)=1.92×10−15 J

4. Relate Kinetic Energy to Energy Gained:
The total kinetic energy gained by the proton after n revolutions is:
KE=n×(qV)
Setting the kinetic energy equal to the energy gained:
2.0875×10−12=n×(1.92×10−15)

5. Solve for n:
n=2.0875×10−121.92×10−15≈1082.64
Rounding to the nearest whole number, we find:
n≈1083

Final Answer:
The number of revolutions made by a proton in a cyclotron to achieve one sixth of the speed of light is approximately 1083.

|
Updated on:8/8/2024
Class 12PHYSICSQUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • Question 1 - Select One

    A car accelerates uniformly from rest to a speed of 10m/s in a time of 5 s .The number of revolutions made by one of its wheels during this motion if the radius of the wheel is 1/π m .

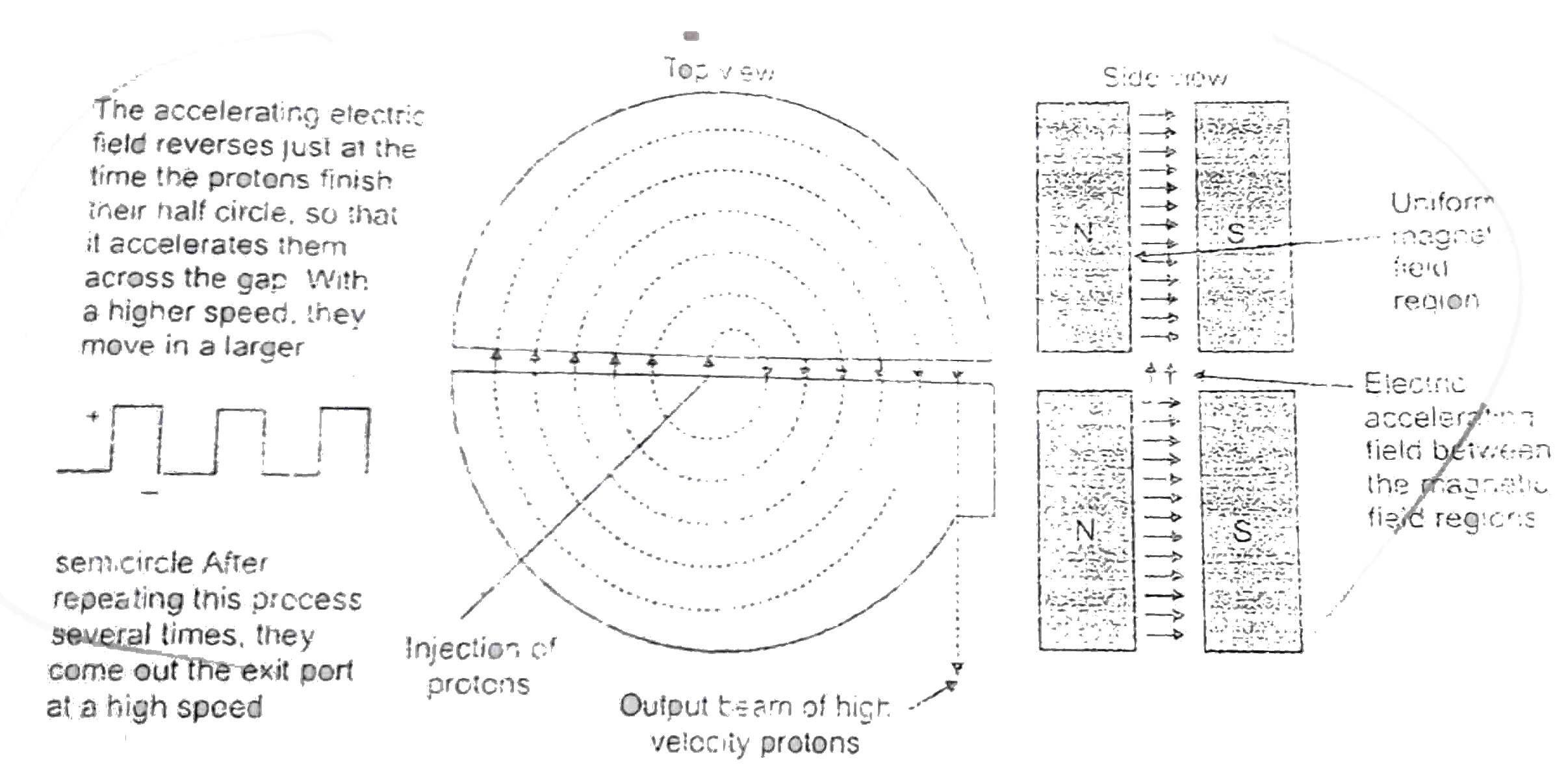
    A50
    B25
    C12.5
    D6.25
  • Question 2 - Select One

    In the given figure of a cyclotron, showing the particle source S and the dees.A uniform magnetic field is directed up form the plane of the page.Circulating protons spiral outward within the hollow dees gaining energy every time they cross the gap between the dees.Suppose that a proton, injected by source S at the centre of the centre of the cyclotron in figure initially moves toward a negatively charged dee.It will accelerate toward this dee and enter it.Once inside, it is shielded from electric field by the copper walls of the dee,that is the electric field does not enter the dee.The magnetic field, however, is not screened by the (nonmagnetic) copper dee, so the proton moves in circular path whose radius, which depends on its speed, is given by
    r=mvqB...(1)
    Let us assume that at the instant the proton emerges into the center gap from the first dee, the potential difference between the dees is reversed.Thus, the proton again faces a negatively charged dee and is again accelerated.Thus,the proton again faces a negatively charged dee and is again accelerated.This process continues, the circulating proton always being in step.with the oscillations of the dee potential, until the proton has spiraled out to the edge of the dee system.There a deflector plate sends it out through a portal.The key to the operation of the cyclotron is that the frequency f at which the proton circulates in the field (and that does not depend on its speed) must be equal to the fixed frequency fosc of the electrical oscilliator, or f=fosc(resonance condition)...(2)
    This resonance condition says that, if the energy of the circulating proton is to increase, energy must be fed to it at a frequency fosc that is equal to the natural frequency f at which the proton circulates in the magnetic field.
    Combining equation 1 and 2 allows us to write the resonance condition as
    qB=2πmfosc..(3)
    For the proton, q and m are fixed.The oscillator (we assume) is designed to work at a single fixed frequency foscWe then "tune" the cyclotron by barying B until eq. 3 is satisfied and then many protons circulate through the magnetic field, to emerge as a beam.
    For a given charge particle a cyclotron can be "tune" by:
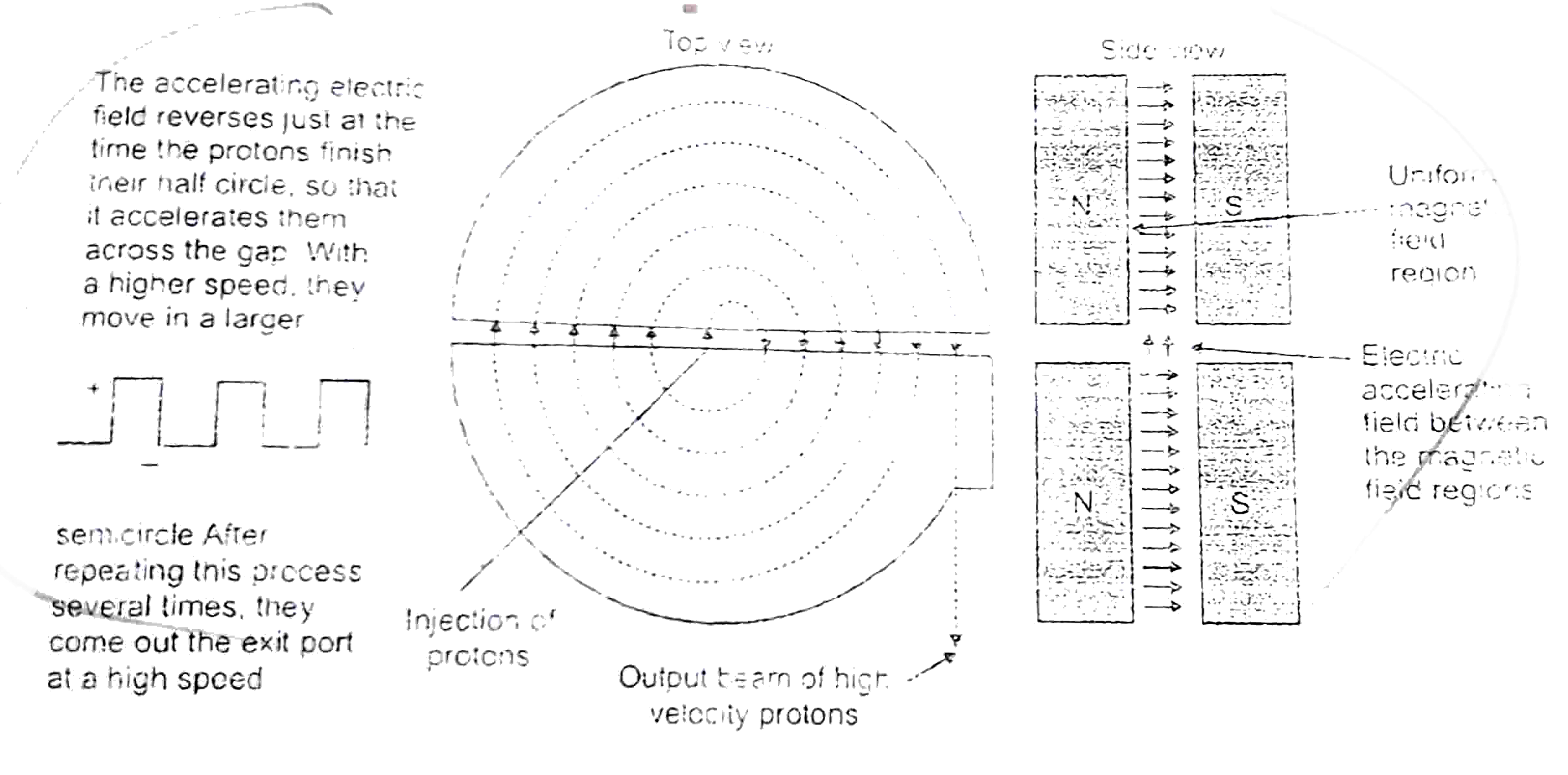
    ocr_image

    Achanging applied A.C. voltange only
    Bchanging applied A.C. voltange and magnetic field both
    Cchanging applied magnetic field only
    Dby changing frequency of applied A.C.
  • Question 3 - Select One

    In the given figure of a cyclotron, showing the particle source S and the dees.A uniform magnetic field is directed up form the plane of the page.Circulating protons spiral outward within the hollow dees gaining energy every time they cross the gap between the dees.Suppose that a proton, injected by source S at the centre of the centre of the cyclotron in figure initially moves toward a negatively charged dee.It will accelerate toward this dee and enter it.Once inside, it is shielded from electric field by the copper walls of the dee,that is the electric field does not enter the dee.The magnetic field, however, is not screened by the (nonmagnetic) copper dee, so the proton moves in circular path whose radius, which depends on its speed, is given by
    r=mvqB...(1)
    Let us assume that at the instant the proton emerges into the center gap from the first dee, the potential difference between the dees is reversed.Thus, the proton again faces a negatively charged dee and is again accelerated.Thus,the proton again faces a negatively charged dee and is again accelerated.This process continues, the circulating proton always being in step.with the oscillations of the dee potential, until the proton has spiraled out to the edge of the dee system.There a deflector plate sends it out through a portal.The key to the operation of the cyclotron is that the frequency f at which the proton circulates in the field (and that does not depend on its speed) must be equal to the fixed frequency fosc of the electrical oscilliator, or f=fosc(resonance condition)...(2)
    This resonance condition says that, if the energy of the circulating proton is to increase, energy must be fed to it at a frequency fosc that is equal to the natural frequency f at which the proton circulates in the magnetic field.
    Combining equation 1 and 2 allows us to write the resonance condition as
    qB=2πmfosc..(3)
    For the proton, q and m are fixed.The oscillator (we assume) is designed to work at a single fixed frequency foscWe then "tune" the cyclotron by barying B until eq. 3 is satisfied and then many protons circulate through the magnetic field, to emerge as a beam.
    If q/m for a charge particle is 106,frequency of applied AC is 106Hz.Then applied magnetic field is
    ocr_image

    A2π tesla
    Bπ tesla
    C2 tesla
    Dcan not be defined