A beaker contains water up to a height h1 and K oil above water up to another height h2. Find the apparent shift in the position of the bottom of the beaker when viewed from above. Refractive index of water is μ1 and that of K oil is μ2.
The apparent shift of the bottom due to the water is △t1=(1−1μ1)h1
and due to the K.oil is
△t2=(1−1μ2)h2
the total shift =△t1+△t2(1−1μ1)h1+(1−μ2)h2
Similar Questions
A vessel contains water up to a height of 20 cm and above it an oil up to another 20 cm. The refractive indices of the water and the oil are 1.33 and F30 respectively. Find the apparent depth of the vessel when viewed from above.
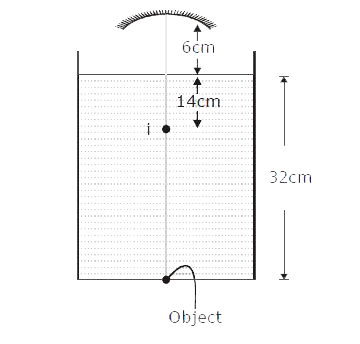
View SolutionA beaker contains water (μ=4/3) filled to a height of 32 cm. A concave mirror is fixed 6 cm above the surface of water as shown in figure. An object is placed at the bottom of the beaker and its image is formed 14 cm below the surface of water. The focal length of the mirror is
View Solution
Knowledge Check
A breaker contains water, up to a height h1 and kerosene of height h2 above water, so that the total height of ( water + kerosene ) is (h1+h2). Refractive index of water is μ1 and that of kerosene is μ2. The apparent shift in the position of the bottom of the beaker when viewed from above is
A(1−1μ1)h2+(1−1μ2)h1B(1+1μ1)h1+(1+1μ2)h2C(1−1μ1)h1+(1−1μ1)h2D(1+1μ1)h2−(1+1μ2)h1A beaker contains water up to a height h1 and kerosene of height h2 above water so that the total height of (water + kerosene) is (h1+h2) . Refractive index of water is μ1 and that of kerosene is μ2 . The apparent shift in the position of the bottom of the beaker when viewed from above is :-
A(1−1μ1)h2B(1−1μ1)h1+(1−1μ2)h2C(1−1μ1)h1D(1+1μ1)h2−(1+1μ2)h1A bird in air looks at a fish vertically below it and inside water. h1 is the height of the bird above the surface of water and h2, the depth of the fish below the surface of water. If refractive index of water with respect to air be μ, then the distance of the fish as observed by the bird is
Ah1+h2Bh1+h2μCμh1+h2Dμh1+μh2
In Fig. a plane mirror lies at a height h above the bottom of a beaker containingwater (refractive index μ) upto a height f. Find the position of the image of the
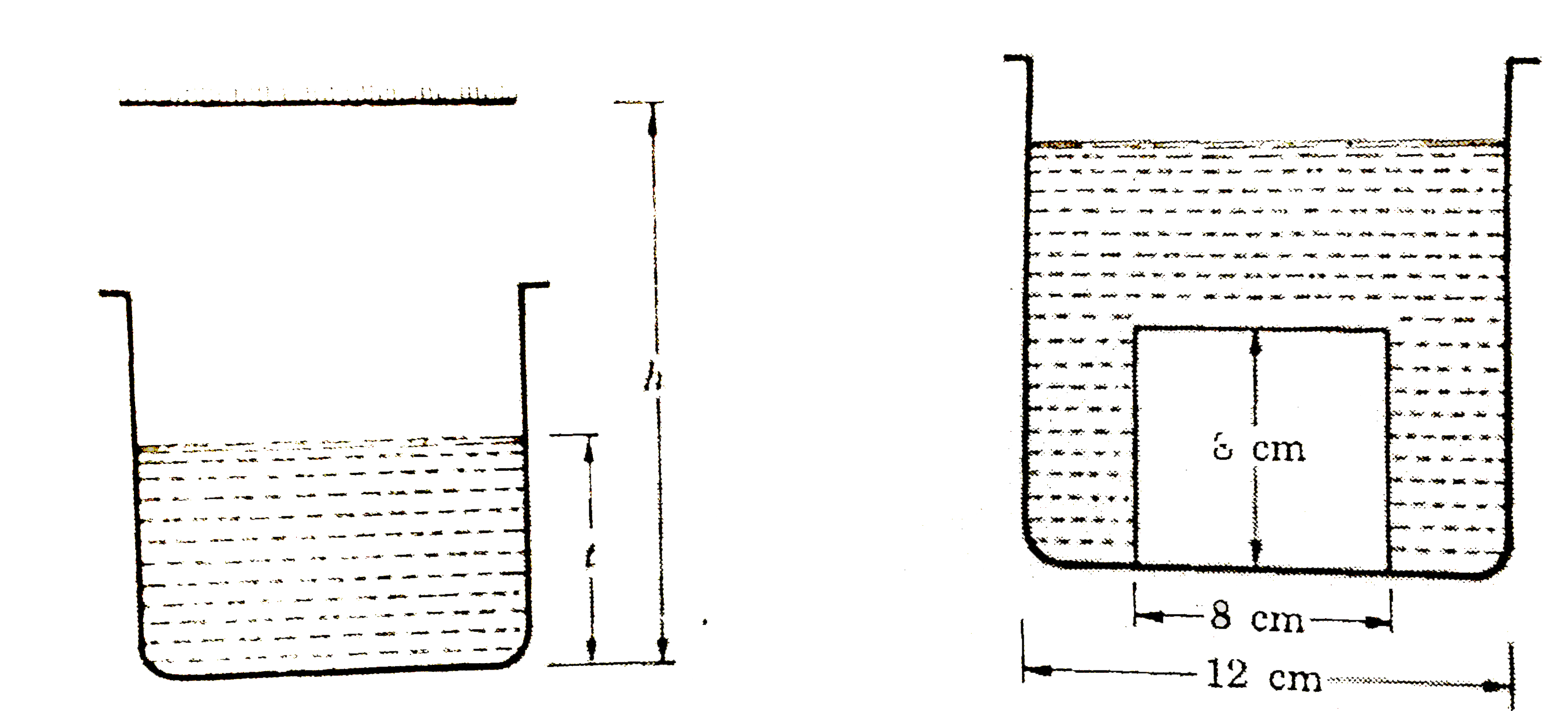
View SolutionBottom of a glass beaker is made of a thin equi-convex lens having bottom side silver polished as shown in the figure. Water is filled in the beaker upto a height 4m. The image of poin to bject,floating at middle point of beaker at the surface of water coincides with it. Find out ther adius of curvature of the lens.Given that refractive index of glass is 3/2 and that of water is 4/3.

View SolutionConsider a tin can of height h as shown in the figure. A coin lies on the botttom at the centre. From the position shown you can barely see the far side of the bottom of the can. When the can is slowly filled with water of refractive index μ, coin is just visible when the can is full. Show that the ratio of the height to radius is
hr=2√μ2−14−μ2

View SolutionA hole is made in the bottom of a container having water filled up to a height h. The velocity of water flowing out of the hole is :
View SolutionWater rises to a height h1 in a capillary tube in a stationary lift. If the lift moves up with uniform acceleration it rises to a height h2, then acceleration of the lift is
View Solution