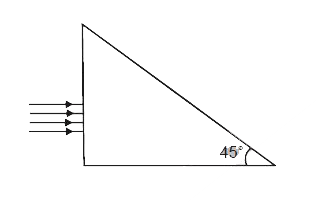
A beam of light consisting of red, green and blue colours is incident on a right angled prism, fig. The refractive indices of the material of the prism for the above red, green and blue wavelengths are 1.39, 1.44 and 1.47 respectively. The prism will
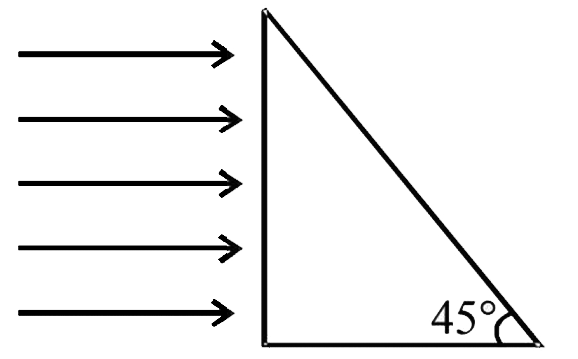
separate part of the colour from the green and blue colours
separate part of the blue colour from the red and green colours
separate all the three colours from one another
not separate even partially any colour from the other two colours
The correct Answer is:A
Step by step video, text & image solution for A beam of light consisting of red, green and blue colours is incident on a right angled prism, fig. The refractive indices of the material of the prism for the above red, green and blue wavelengths are 1.39, 1.44 and 1.47 respectively. The prism will by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Three light rays red (R), green (G) and blue (B) are incident on a right angled prism 'abc' at face 'ab'. The refractive indices of the material of the prism for red, green and blue wavelengths are 1.39 , 1.44 and 1.47 respectively. Out of the time three which colour ray will emerge out of face 'ac' ? Justify your answer. Trace the path of these rays after passing through face 'ab'

View SolutionThree rays of light, namely red (R), green (G) and blue (B) are incident on the face PQ of a right angled prism PQR as showns in the figure.
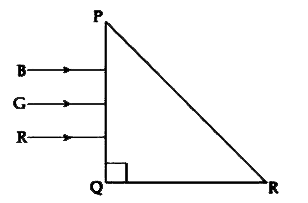
The refractive indices of the material of the prism for red green and blue wavelength are 1.27, 1.42 and 1.49 respectively. The colour of the ray(s) emerging out of the face PR is:
View Solution
Knowledge Check
A beam of light consisting of red, green and blue colours is incident on right angled prism. The refractive indices of the material of the prism for the above red, green and blue wavelengths are 1.39,1.44and1.47 respectively. The prism will.
 .ASeparate the red colour part from green and blue colours.BSeparate the blue colour part from the red and green colours.CSeparate all the three colours from one another.DNot separate the three colours at all.
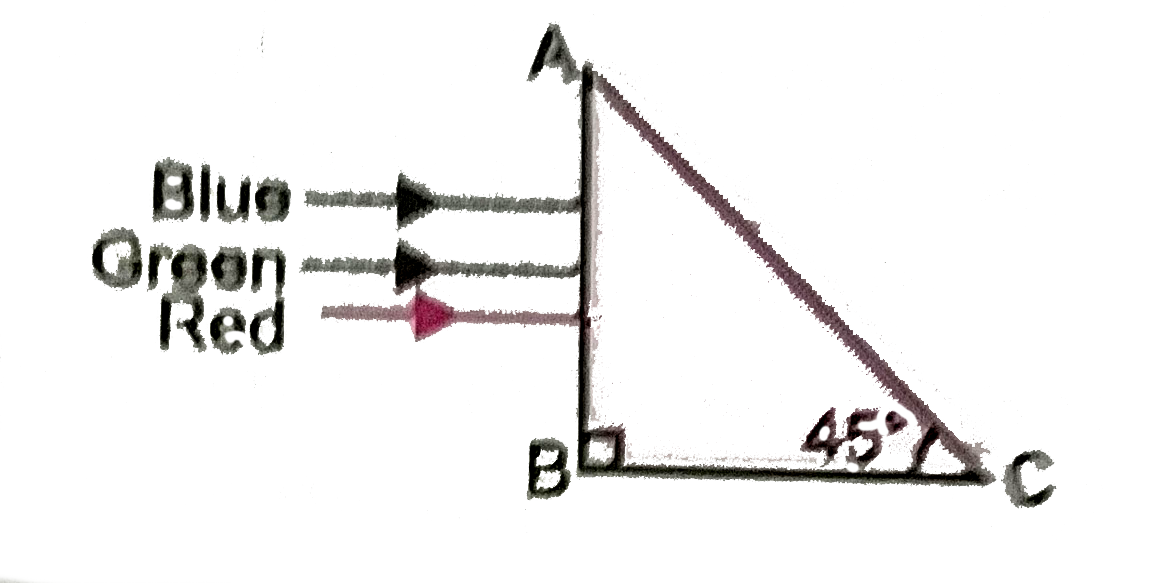
.ASeparate the red colour part from green and blue colours.BSeparate the blue colour part from the red and green colours.CSeparate all the three colours from one another.DNot separate the three colours at all.A beam of light consisting of red, green, and blue colors is incident on a right-angled prism. The refractive indices of the material of the prism for the above red, green and blue wavelengths are 1.39, 1.44 and 1.47, repectively. The prism will
 Aseparate part of the red color from the green and blue colorsBseparate part of the blue color from the red and green colorsCseparate all the three colors from one anotherDnot separate even partially any color from the other two colors
Aseparate part of the red color from the green and blue colorsBseparate part of the blue color from the red and green colorsCseparate all the three colors from one anotherDnot separate even partially any color from the other two colorsA beam of light consisting of red, green and blue colours is incident on a right angled prism. The refractive index of the material of the prism for the above red, green and blue wavelengths are 1.39, 1.44 and 1.47, respectively.
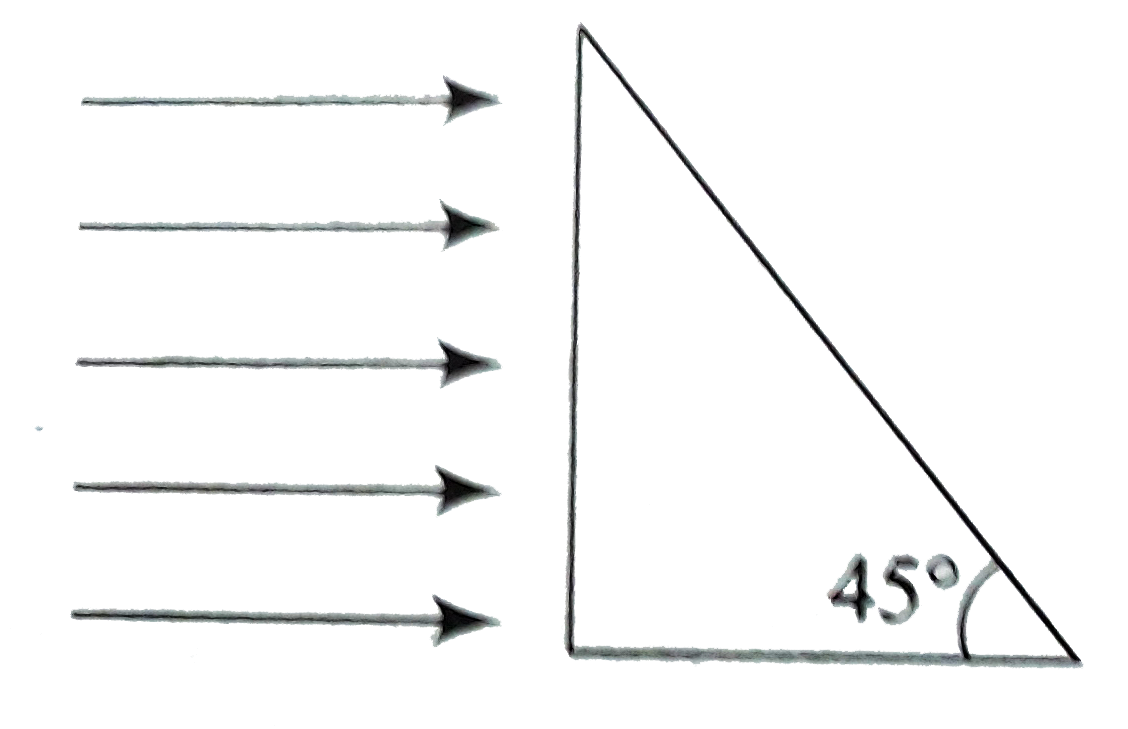
 Aseparate the blue colour part from the red and green coloursBseparate all the three colours from one anotherCnot separtate the three colours at allDseparate the red colour part from the green and blue colours
Aseparate the blue colour part from the red and green coloursBseparate all the three colours from one anotherCnot separtate the three colours at allDseparate the red colour part from the green and blue colours
A beam of light consisting of red, green and blue and is incident on a right angled prism. The refractive index of the material of the prism for the above red, green and blue wavelengths are 1.39, 1.44 and 1.47 respectively. The prism will :
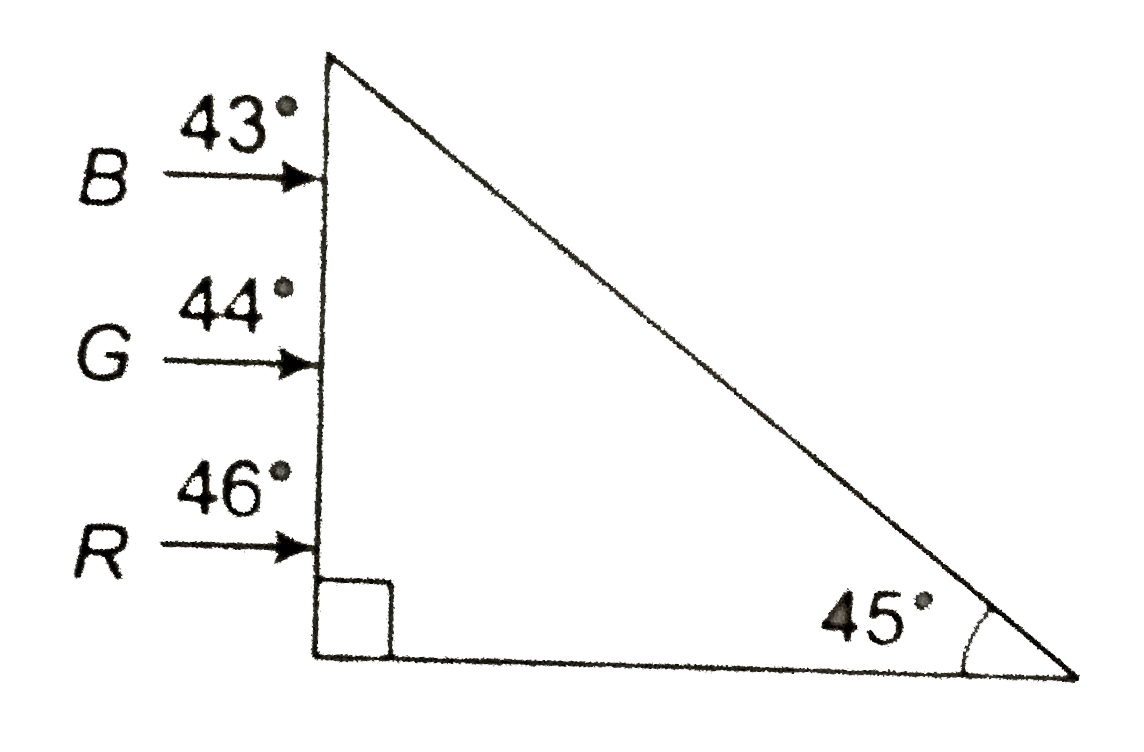
View SolutionFigure shows a mixture of blue, green and red coloured rays incident normally on a right angled prism. The critical angles of the material of the prism for red, green and blue are 46∘, 44∘ and 43∘ respectively. The arrangement will separate
View SolutionA ray of light containing both red and blue colours is incident on the refracting surface of a prism. Then.
View SolutionA thin glass prism has a refracting angle 6∘ . The refractive indices of the material of the prism for red and violet colours are 1.56 and 1.6 respectively . What is the angular dispersion ?
View SolutionIf the refractive indices of a prism for red, yellow and violet colours be 1.61,1.63 and 1.65 respectively, then the dispersive power of the prism will be
View Solution
