A beam of light has two wavelengths 4,972Åand6,216Å with a total intensity of 3.6×10−3Wm−2 equally distributed among the two wavelengths . The beam falls normally on an area of 1cm2 of clean metallic surface of work function 2.3 eV . Assume that there is no loss of light by reflection and that each capable photon ejects one electron. The number of photoelectrons liberated in 2 s is approximately
6×1011
9×1011
11×1011
15×1011
The correct Answer is:B
To solve the problem step by step, we will follow these steps:
Step 1: Determine the Intensity for Each Wavelength
The total intensity of the beam is given as 3.6×10−3W/m2. Since the intensity is equally distributed among the two wavelengths, we can calculate the intensity for each wavelength as follows:
I1=I2=3.6×10−32=1.8×10−3W/m2
Step 2: Calculate the Energy of Photons for Each Wavelength
The energy of a photon can be calculated using the formula:
E=hcλ
Where:
- h=6.63×10−34J s (Planck's constant)
- c=3×108m/s (speed of light)
- λ is the wavelength in meters.
First, we convert the wavelengths from angstroms to meters:
- λ1=4972Å=4972×10−10m
- λ2=6216Å=6216×10−10m
Now we can calculate the energy for each wavelength:
For λ1:
E1=(6.63×10−34)×(3×108)4972×10−10=2.49eV
For λ2:
E2=(6.63×10−34)×(3×108)6216×10−10=1.994eV
Step 3: Determine Which Wavelength Can Eject Electrons
The work function (ϕ) of the metallic surface is given as 2.3eV. We compare the energies of the photons with the work function:
- For λ1: E1=2.49eV>2.3eV (can eject electrons)
- For λ2: E2=1.994eV<2.3eV (cannot eject electrons)
Thus, only photons of wavelength λ1 can eject electrons.
Step 4: Calculate the Number of Photons Incident on the Surface
The number of photons incident on the surface can be calculated using the formula:
N=I⋅A⋅tE
Where:
- I=1.8×10−3W/m2 (intensity for λ1)
- A=1cm2=1×10−4m2 (area)
- t=2s (time)
- E=2.49eV=2.49×1.6×10−19J (energy of a photon in joules)
Calculating E:
E=2.49×1.6×10−19=3.984×10−19J
Now substituting into the formula for N:
N=(1.8×10−3)⋅(1×10−4)⋅23.984×10−19
Calculating N:
N=3.6×10−73.984×10−19≈9.04×1011
Step 5: Conclusion
The total number of photoelectrons liberated in 2 seconds is approximately 9×1011.
---
The total intensity of the beam is given as 3.6×10−3W/m2. Since the intensity is equally distributed among the two wavelengths, we can calculate the intensity for each wavelength as follows:
The energy of a photon can be calculated using the formula:
- h=6.63×10−34J s (Planck's constant)
- c=3×108m/s (speed of light)
- λ is the wavelength in meters.
- λ1=4972Å=4972×10−10m
- λ2=6216Å=6216×10−10m
E1=(6.63×10−34)×(3×108)4972×10−10=2.49eV
E2=(6.63×10−34)×(3×108)6216×10−10=1.994eV
The work function (ϕ) of the metallic surface is given as 2.3eV. We compare the energies of the photons with the work function:
- For λ2: E2=1.994eV<2.3eV (cannot eject electrons)
The number of photons incident on the surface can be calculated using the formula:
- I=1.8×10−3W/m2 (intensity for λ1)
- A=1cm2=1×10−4m2 (area)
- t=2s (time)
- E=2.49eV=2.49×1.6×10−19J (energy of a photon in joules)
E=2.49×1.6×10−19=3.984×10−19J
N=(1.8×10−3)⋅(1×10−4)⋅23.984×10−19
N=3.6×10−73.984×10−19≈9.04×1011
The total number of photoelectrons liberated in 2 seconds is approximately 9×1011.
Topper's Solved these Questions
- DUAL NATURE OF RADIATION AND MATTER BOOK - MODERN PUBLICATIONCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - COMPETITION FILE (OBJECTIVE TYPE QUESTIONS ( B - Multiple Choice Questions) (JEE (Advanced) for IIT Entrance))
15 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - MODERN PUBLICATIONCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - COMPETITION FILE (OBJECTIVE TYPE QUESTIONS ( C - Multiple Choice Questions) )
8 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - MODERN PUBLICATIONCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - COMPETITION FILE (OBJECTIVE TYPE QUESTIONS ( B - Multiple Choice Questions) (AIPMT/NEET & Other State Boards for Medical Entrance))
26 Videos
- CURRENT ELECTRICITYBOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - Chapter Practice Test
15 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - MODERN PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - Chapter Practice Test
15 Videos
Similar Questions
A beam of light has three wavelengths 4144Å, and 6216Å with a total instensity of 3.6×10−3Wm−2 equally distributed amongst the three wavelengths. The beam falls normally on an area 1.0cm2 of a clean metallic surface of work function 2.3 eV. Assume that there is no loss of light by reflection number of photoelectrons liberated in two seconds.
View SolutionA beam of light has three λ,4144Å,4972Åand6216Å with a total intensity of 3.6×10−3Wm−2 equally distributed amongst the three λ. The beam falls normally on an area 1.0cm2 of a cleam metallic surface of work function 2.3 eV. Assume that there is no loss of light by reflection etc. Calculate the no. of photoelectrons emitted in 2 sec, in scientific notation,x×10y find the value of y.
View Solution
Knowledge Check
A beam of light has three λ,4144Å,4972Åand6216Å with a total intensity of 3.6×10−3Wm−2 equally distributed amongst the three λ. The beam falls normally on an area 1.0cm2 of a cleam metallic surface of work function 2.3 eV. Assume that there is no loss of light by reflection etc. Calculate the no. of photoelectrons emitted in 2 sec, in scientific notation,x×10y find the value of y.
A2×109B1.075×1012C9×108D3.75×106A light beam of intensity 3.3×10−3jm2-s and wavelength 6000A∘ falls normally on a photosensitive surface of area 2cm2 and work function 2.0 eV assuming that there is no light loss due to reflection match the result given in column II for the physical quantities given in column I
 A
A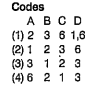 B
B C
C D
D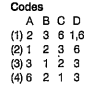
A beam of light has three wavelengths 4000Å,5000Å,6000Å with a total intensity 3×10−3W/m2 equally distributed amongst the three wavelenth. The beam falls normally on an area 2cm2 of clean metallic surface of work function 2.4eV. Calculate photo current. (Assume each energetically suitable photon emits one electron)
View SolutionA beam of light consists of four wavelength 4000Å,4800A,6000A and 7000Å, each of intensity 1.5×10−3Wm−2. The beam falls normally on an area 10−4m2 of a clean metalic surface of work function 1.9eV. Assuming no loss of light energy (i.e. each capable photon emits one electron) calculate the number of photoelectrons liberated per second.
View SolutionA beam of light has an power of 144 W equally distributed among three wavelengths of 4100Å, 4960Å and 6200Å. The beam is incident at an angle of incidence of 60° on an area of 1cm2 of a clean sodium surface, having a work function of 2.3 eV.Assuming that there is no loss of light by reflection and that each energetically capable photon ejects a photoelectron, find the saturation photocurrent. (Take hc/e=12400eVÅ)
View SolutionLight of wavelength 3000 Å falls on a metal surface having work function 2.3 eV. Calculate the maximum velocity of ejected electrons.
(Planck's constant , h=6.63×10−34 J.s. , velocity of light c=3×108m/s , mass of an electron = 9.1×10−31 kg )
View SolutionLight of wavelenght 5000Å fall on a metal surface of work function 1.9eV Find
a. The energy of photon
b. The kinetic energy of photoelectrons
View SolutionLight of wavelength 2000 Å falls on a metallic surface whose work function is 4.21 eV. Calculate the stopping potential
View Solution
