A bicyclist is riding at a constant speed along a straight-line path. The rider throws a ball straight up to a height a few meters above her head. Ignoring air resistance, where will the ball land?
Behind the rider
In front of the rider
In the same hand that threw the ball
In the opposite hand to the one that threw it.
The correct Answer is:C
To solve the problem of where the ball will land when thrown straight up by a bicyclist moving at a constant speed, we can break it down into a few logical steps:
1. Understanding the Initial Conditions:
- The bicyclist is moving at a constant speed (let's denote this speed as V).
- The ball is thrown straight up from the bicyclist's hand.
2. Analyzing the Motion of the Ball:
- When the ball is thrown upward, it has an initial vertical velocity (let's denote this as Vy0), which is the speed at which the ball is thrown upwards.
- However, the ball also retains the horizontal velocity of the bicyclist, which is V.
3. Vertical Motion:
- The vertical motion of the ball will be influenced by gravity, which acts downward with an acceleration of g.
- The ball will rise to a maximum height, where its vertical velocity becomes zero, and then it will fall back down.
4. Horizontal Motion:
- Since there is no horizontal acceleration acting on the ball (ignoring air resistance), it will continue to move horizontally at the same speed V as the bicyclist.
- This means that while the ball is in the air, it will travel horizontally the same distance as the bicyclist.
5. Time of Flight:
- The time the ball spends in the air is determined by its vertical motion. It will take some time to reach the maximum height and then the same amount of time to fall back down.
- During this time, the bicyclist continues to move forward at speed V.
6. Conclusion:
- Since both the ball and the bicyclist have the same horizontal velocity, when the ball comes back down, it will land directly back in the hand of the bicyclist.
Final Answer:
The ball will land directly back in the hand of the bicyclist.
---
- The bicyclist is moving at a constant speed (let's denote this speed as V).
- The ball is thrown straight up from the bicyclist's hand.
- When the ball is thrown upward, it has an initial vertical velocity (let's denote this as Vy0), which is the speed at which the ball is thrown upwards.
- However, the ball also retains the horizontal velocity of the bicyclist, which is V.
- The vertical motion of the ball will be influenced by gravity, which acts downward with an acceleration of g.
- The ball will rise to a maximum height, where its vertical velocity becomes zero, and then it will fall back down.
- Since there is no horizontal acceleration acting on the ball (ignoring air resistance), it will continue to move horizontally at the same speed V as the bicyclist.
- This means that while the ball is in the air, it will travel horizontally the same distance as the bicyclist.
- The time the ball spends in the air is determined by its vertical motion. It will take some time to reach the maximum height and then the same amount of time to fall back down.
- During this time, the bicyclist continues to move forward at speed V.
- Since both the ball and the bicyclist have the same horizontal velocity, when the ball comes back down, it will land directly back in the hand of the bicyclist.
The ball will land directly back in the hand of the bicyclist.
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - MOTION IN TWO AND THREE DIMENSIONSEXERCISE - PRACTICE QUESTIONS (MORE THAN ONE CORRECT CHOICE TYPE)3videos
MOTION IN TWO AND THREE DIMENSIONS
- BOOK - RESNICK AND HALLIDAYCHAPTER - MOTION IN TWO AND THREE DIMENSIONSEXERCISE - PRACTICE QUESTIONS (LINKED COMPREHENSION)14videos
MOTION IN TWO AND THREE DIMENSIONS
- BOOK - RESNICK AND HALLIDAYCHAPTER - MOTION IN TWO AND THREE DIMENSIONSEXERCISE - PROBLEMS50videos
MOTION IN TWO AND THREE DIMENSIONS
- BOOK - RESNICK AND HALLIDAYCHAPTER - MOTION ALONG A STRAIGHT LINEEXERCISE - PRACTICE QUESTIONS ( Integer Type )3videos
MOTION ALONG A STRAIGHT LINE
- BOOK - RESNICK AND HALLIDAYCHAPTER - OSCILLATIONSEXERCISE - Practice Questions57videos
OSCILLATIONS
Similar Questions
A ball rools at constant speed in a straight line along the ground. Jerry kicks the ball in the direction of its motion. As a result of Jerry's kick, speed of the ball will
View SolutionA man is standing on a rail road car travelling with a constant speed of v=10ms−1 (Fig . 5.34). He wishes to throw a ball through a stationary hoop 5m above the height of his hands in such a manner that the ball will move horizontally as it passes through the hoop. He throws the ball with a speed of 12.5ms−1 w.r.t. himself.
(a) What must be the vertical component of the initial velocity of the ball ?
(b) How many seconds after he releases the ball will it pass through the hoop ?
( c) At what horizontal distance in front of the loop must he release the ball ?
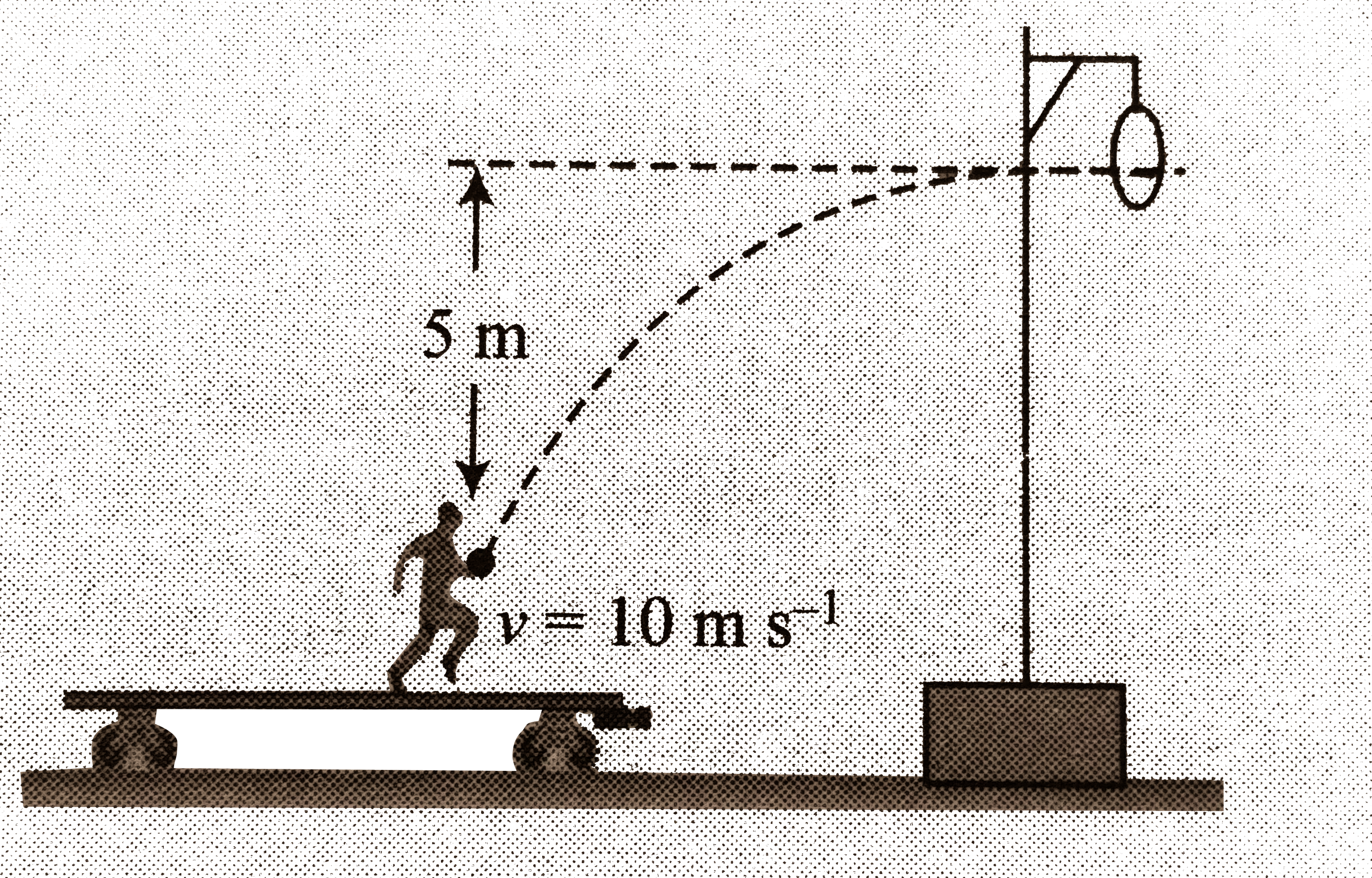 .View Solution
.View Solution
Knowledge Check
- Question 1 - Select One
A particle is moving with a constant speed along a straight line path. A force is not requied to
Aincreased its speedBDecrease the momentumCchange the directionDkeep it moving with uniform velocity - Question 2 - Select One
A particle is moving with a constant speed along a straight line path. A force is not required to
AIncrease its speedBDecrease the momentumCChange the directionDKeep it moving with uniform velocity - Question 3 - Select One
A person sitting in a train moving with a constant velocity along a straight line throws a ball vertically upwards, then the ball will
Afull onwards the trainBbehind the thrower's handCreturn to thrower's handDnothing can be decided
A man of height h is walking at constant speed v0 along edge of a straight horizontal road. There is a lamp post of height H=2h on the other edge as shown. If speed of tip of shadow of his head is nv0 then find n.
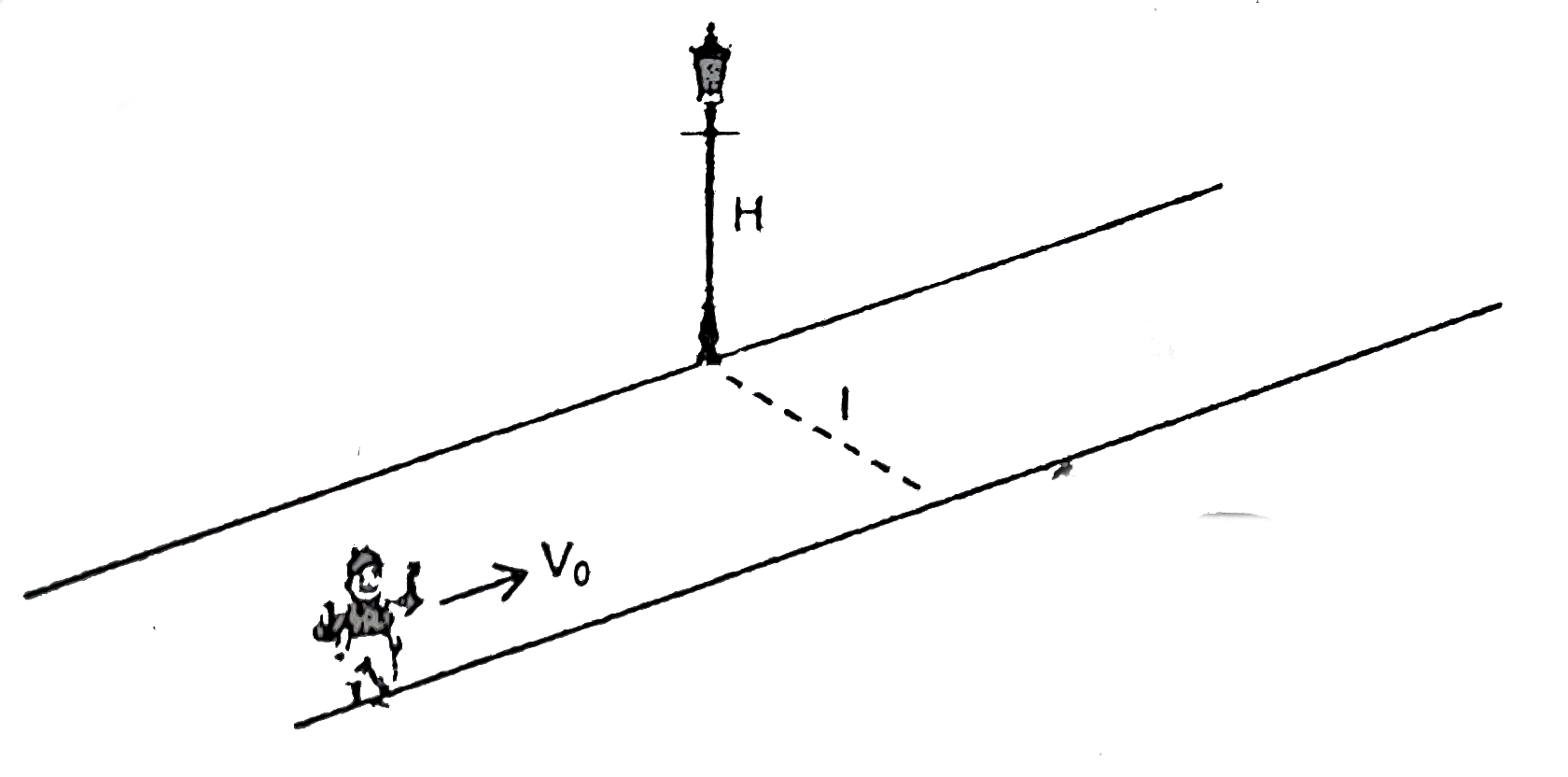 View Solution
View SolutionA man is riding on a flat car travelling with a constant speed of 10m/s.He wishes to throw a ball through a stationary hoop 15m above the height of his hands in such a manner that the ball will move horizontally as it passes through the hoop. He throws the ball with a speed of 12.5m/s w.r.t himself.
How many seconds after he release the ball will it pass through the hoop?View SolutionA man is riding on a flat car travelling with a constant speed of 10m/s.He wishes to throw a ball through a stationary hoop 15m above the height of his hands in such a manner that the ball will move horizontally as it passes through the hoop. He throws the ball with a speed of 12.5m/s w.r.t himself.
At what horizontal distance in front of the hoop must he release the ball?View SolutionA basketball player is running at a constant speed of 2.5 m/s when a player tosses a basketball upward with a speed of 6.0 m/s. How far does the player run before he catches the ball? Ignore air resistance.
View SolutionA ball is thrown straight upward with a speed v from a point h meter above the ground. The time taken for the ball to strike the ground is
View Solution

