A man of height h is walking at constant speed v0 along edge of a straight horizontal road. There is a lamp post of height H=2h on the other edge as shown. If speed of tip of shadow of his head is nv0 then find n. 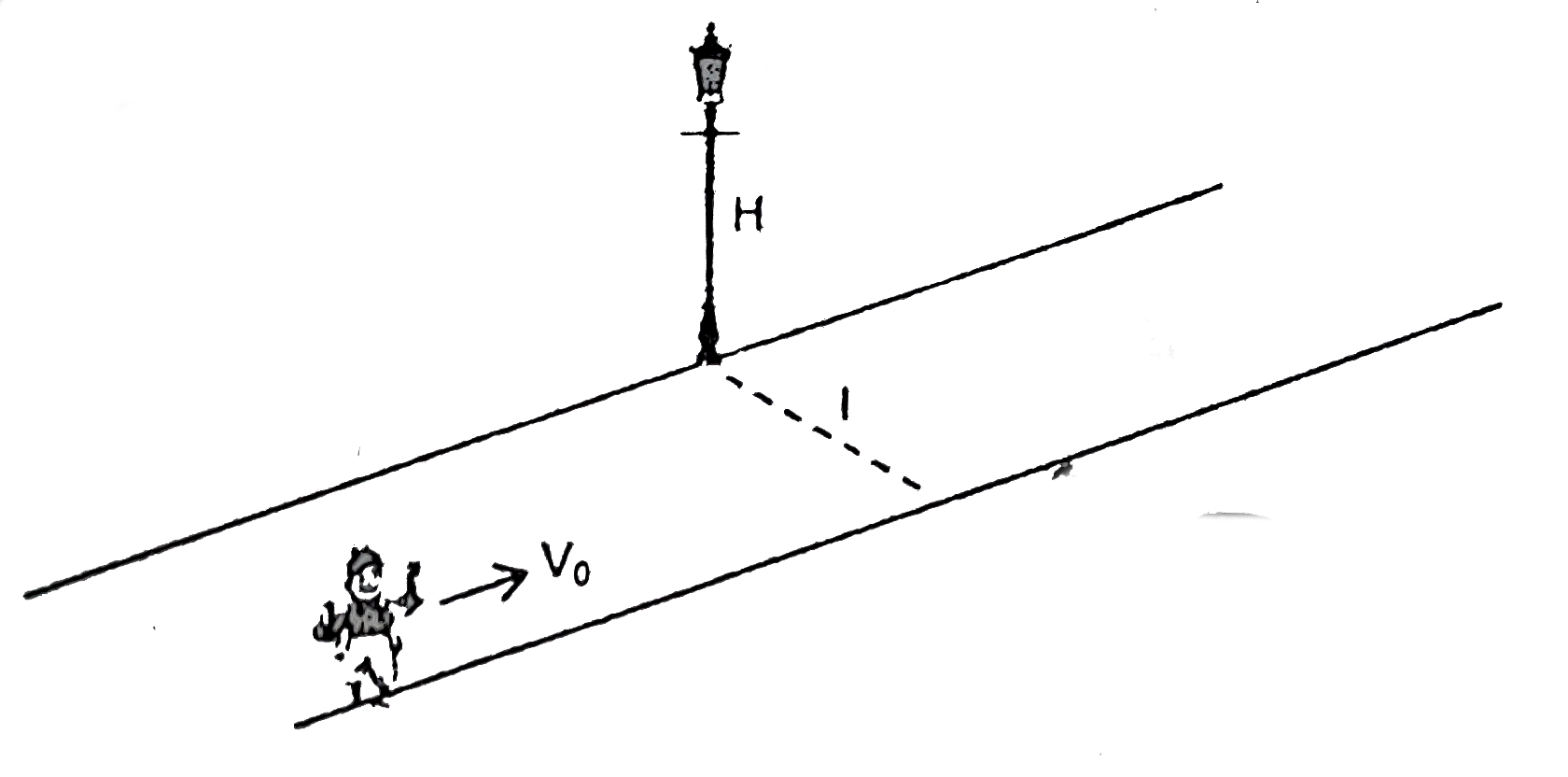
The correct Answer is:2
x=HH−hI 
y=(HH−h)y′
dxdt=0 & dydt=(HH−h)V0
Topper's Solved these Questions
Similar Questions
A person of height 1.6m is walking away from a lamp post of height 4 m along a straight path on the flat ground. The lamp post and the person are always perpendicular to the ground. If the speed of the person is 60cms−1, the speed of the tip of the person’s shadow on the ground with respect to the person is _______ cms−1 .
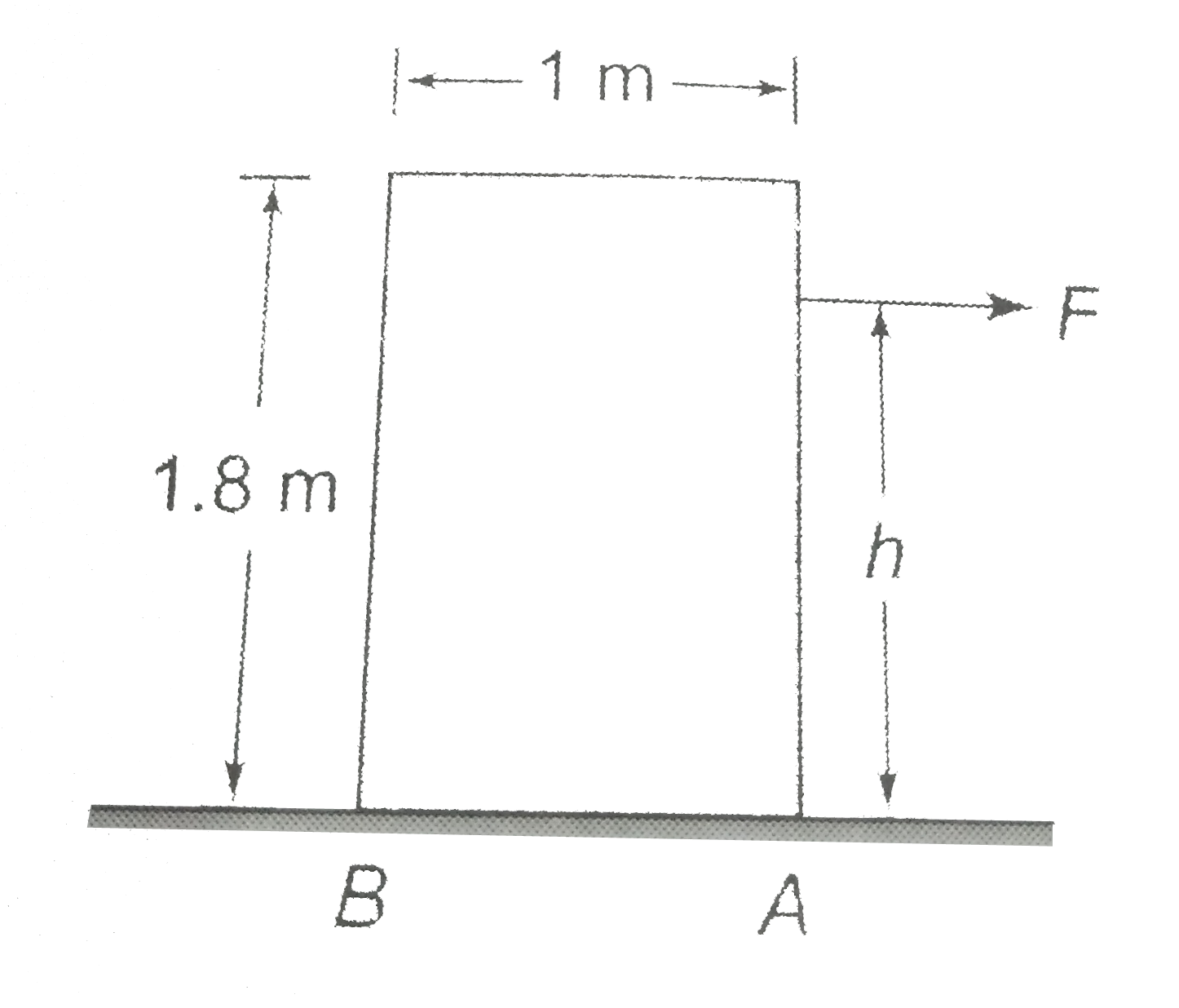
View SolutionA rectangular block of square base (1m×1m) and height 1.8m is moving with constant speed on a rough horizontal surface (μk=0.5) due to horizontal force F as shown. If the mass of block is 40kg, find
(a) the value of F1
(b) the value of h at which the block just starts to tip
(c) If force F is applied at h/2, find the perpendicular distance of normal reaction from O (center of mass).
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A man of height h walks in a straight path towards a lamp post of height H with uniform velocity u. Then , the velocity of the edge of the shadow on the ground will be
AhuH−hBHuH+hCH−hHuDH+hHu - Question 2 - Select One
A man of height h walks in a straight path towards a lamp post of height H with uniform velocity u. Then , the velocity of the edge of the shadow on the ground will be
AhuH−hBHuH+hCH−hHuDH+hHu - Question 3 - Select One
man of height h walks in a straight path towards a lamp post of height H with uniform velocity u. Then the velocity of the edge of the shadow on the ground will be :-
AHu(H−h)BHu(H+h)C(H−h)HuD(H+h)Hu
A man of height 'h' is walking away from a street lamp with a constant speed 'v'. The height of the street lamp is 3h. The rate at which the length of the man's shadow is increasing when he is at a distance 10 h from the base of the street lamp is
View SolutionA 2−m wide truck is moving with a uniform speed v0=8ms−1 along a straight horizontal road. A pedestrian starts to cross the road with a uniform speed v when the truck is 4m away from him, The minimum value of v so that he can cross the road safely is .
View SolutionA man of height 'h'is walking away from a street lamp with a constant speed'v'.The height of the street lamp is 3hThe rate at which of the length of man's shadow is increasingwhen he is at a distance 10hfrom the base of the street lamp is:
View SolutionA 2−m wide truck is moving wigh a uniform speed v0=8ms−1 along a straight horizontal road. A pedestrian starts to cross the road with a uniform speed v when the truck is 4m away from him, The minimum value of v so that he can cross the road safely is .
View SolutionA man of height 2m walks directly away from a lamp of height 5 m on a level road at 3m/s. The rate at which the length of his shadow is increasing is
View Solution

