
A billiard ball, initially at rest, is given a sharp impulse by a cue. The cue is held horizontally a distance above the centre line as shown in figure. The ball leaves the cue with a speed and because of its backward slipping eventually acquires a final
speed show that
Where is the radius of the ball.
Let be the linear velocity and be the angular velocity imparted.
Linear impulse
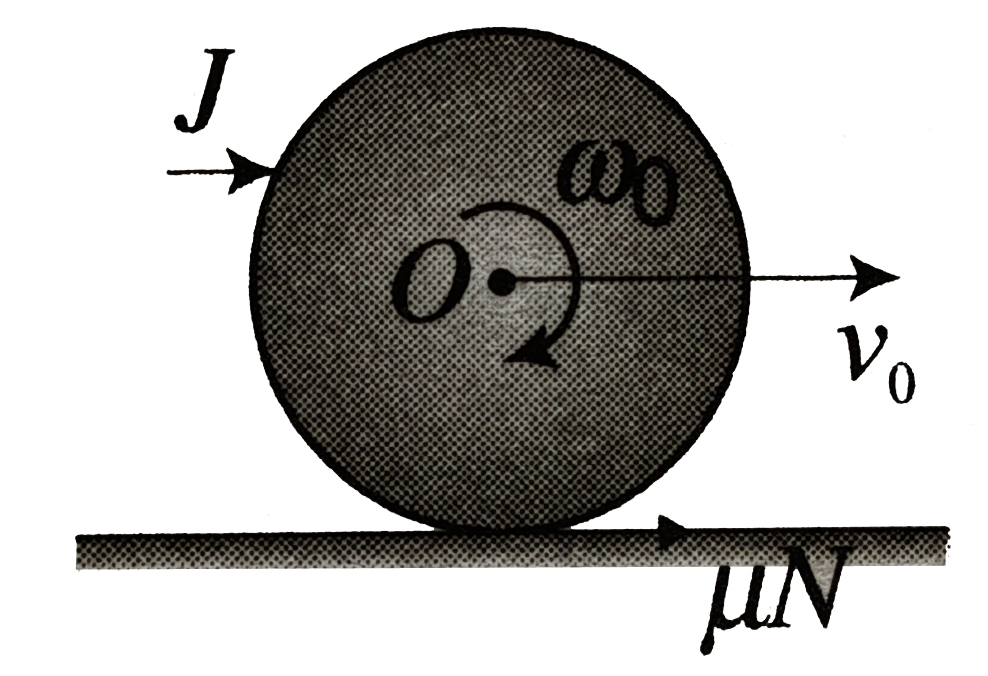
Angular impulse
..........i
As the linear velocity increases to , friction must be in forwrd directiion and hence it opposes angular motion.
For lilnear motion. Friction increases the velocity. Hecne,
Let be the time when rolling starts.
For rotation: Friction torque opposes rotation and hence decreases .
After time
Combining all the equations, we get
(eliminating )
Substituting for from eqn i we get
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Solved Examples12videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Exercise 3.111videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer11videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer16videos
SOUND WAVES AND DOPPLER EFFECT
Similar Questions

A billiard ball, initially at rest, is given a sharp impulse by a cue. The cue is held horizontally a distance h above the centre line as shown in figure. The ball leaves the cue with a speed v0 and because of its forward english (backward slipping) eventually acquires a final
speed 97v0 show that h=45R
Where R is the radius of the ball.View SolutionThe cue stick hits a cue ball horizontally a distance x above the centre of the ball. Find the value of x for which the cue ball will instantaneously roll without slipping. Calculate the answer in terms of the radius R of the ball.
 View Solution
View SolutionA billiard ball of mass m and radius r, when hit in a horizontal direction by a cue at a height h above its centre, acquired a linear velocity v0. The angular velocity ω0 acquired by the ball is
View Solution_E01_216_Q01.png)
A syringe containing water is held horizontally with its nozzle at a height h above the ground as shown in fig the cross sectional areas of the piston and the nozzle are A and a respectively the piston is pushed with a constant speed v. Find the horizontal range R of the stream of water on the ground.View SolutionA uniform disc of radius R is in pure rolling on a fixed horizontal surface with constant speed v0 as shown in the figure. For what value of θ, speed of point P will be v02√(5+2√3) ? (OP= R/2 and O is the centre of disc)
 View Solution
View SolutionFive balls are placed one after the other along a straight line as shown in the figure. Initially, all the balls are at rest. Then the second ball has been projected with speed v0 towards the third ball. Mark the correct statements, (Assume all collisions to be head-on and elastic.)
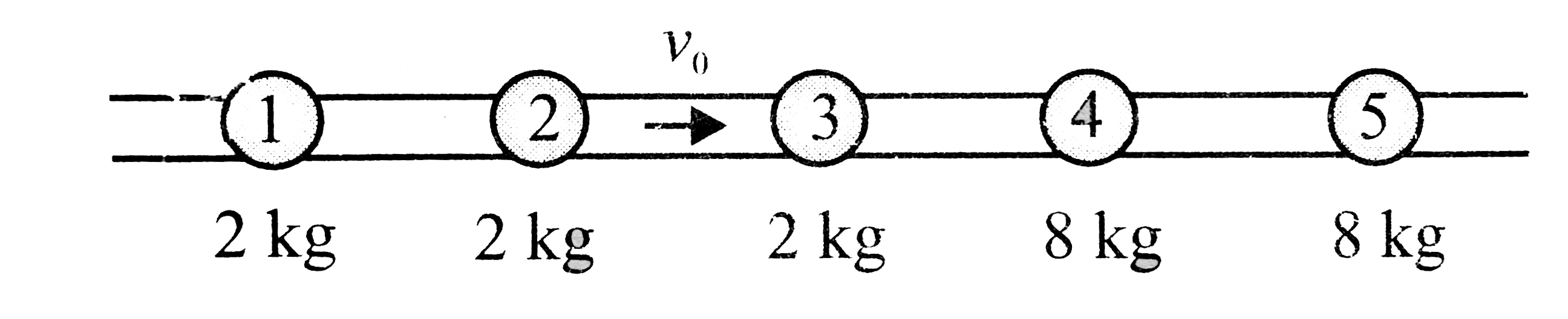 View Solution
View SolutionA solid spherical ball of radius R collides with a rough horizontal surface as shown in figure. At the time of collision its velocity is v0 at an angle θ to the horizontal and angular velocity ω0 as shown . After collision, the angular velocity of ball may
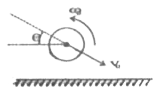 View Solution
View SolutionTwo motor boats A and B move from same point along a circle of radius 10 m in still water. The boats are so designed that they can move only with constant speeds. The boats A and B take 16 and 8 sec respectively to complete one circle in stationary water. Now water starts flowing at t=0 with a speed 4ms in a fixed direction. Find the distance between the boats after t=8 sec.
View Solution(a) With what velocity (v0) should a ball be projected horizontally from the top of a tower so that the horizontal distance on the ground is ηH, where H is the height of the tower ?
(b) Also determine the speed of the ball when it reaches the ground.
 .View Solution
.View SolutionA horizontal circular platform of radius 0.5 m and mass axis. Two massless spring toy-guns, each carrying a steel ball of mass 0.05 kg are attached to the platform at a distance 0.25m from the centre on its either sides along its diameter (see figure). Each gun simultaneously fires the balls horizontally and perpendicular to the diameter in opposite directions. After leaving the platform, the balls have horizontal speed of 9ms−1 with respect to the ground. The rotational speed of the platform in rads−1 after the balls leace the platform is
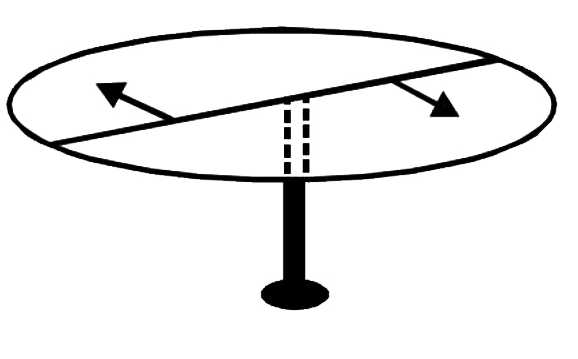 View Solution
View Solution
