A uniform disc of radius R is in pure rolling on a fixed horizontal surface with constant speed v0 as shown in the figure. For what value of θ, speed of point P will be v02√(5+2√3) ? (OP= R/2 and O is the centre of disc) 
30°
45°
60°
53°
Step by step video & image solution for A uniform disc of radius R is in pure rolling on a fixed horizontal surface with constant speed v_0 as shown in the figure. For what value of theta, speed of point P will be v_0/2√(5+2√3) ? (OP= R/2 and O is the centre of disc) by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
A disc of radius R is rolling purely on a flat horizontal surface, with a constant angular velocity. The angle between the velocity ad acceleration vectors of point P is

View Solution
A disc of radius R is rolling purely on a flat horizontal surface, with a constant angular velocity the angle between the velocity ad acceleration vectors of point P is
View SolutionA disc of radius R is moving on a rough horizontal surface with velocity v and angular speed ω at an instant as shown in figure. Choose the correct statement.

View SolutionA disc of radius R is rolling purely on a flat horizontal surface, with a constant angular velocity. The angle between the velocity and acceleration vectors of point P is
 .
.
View Solution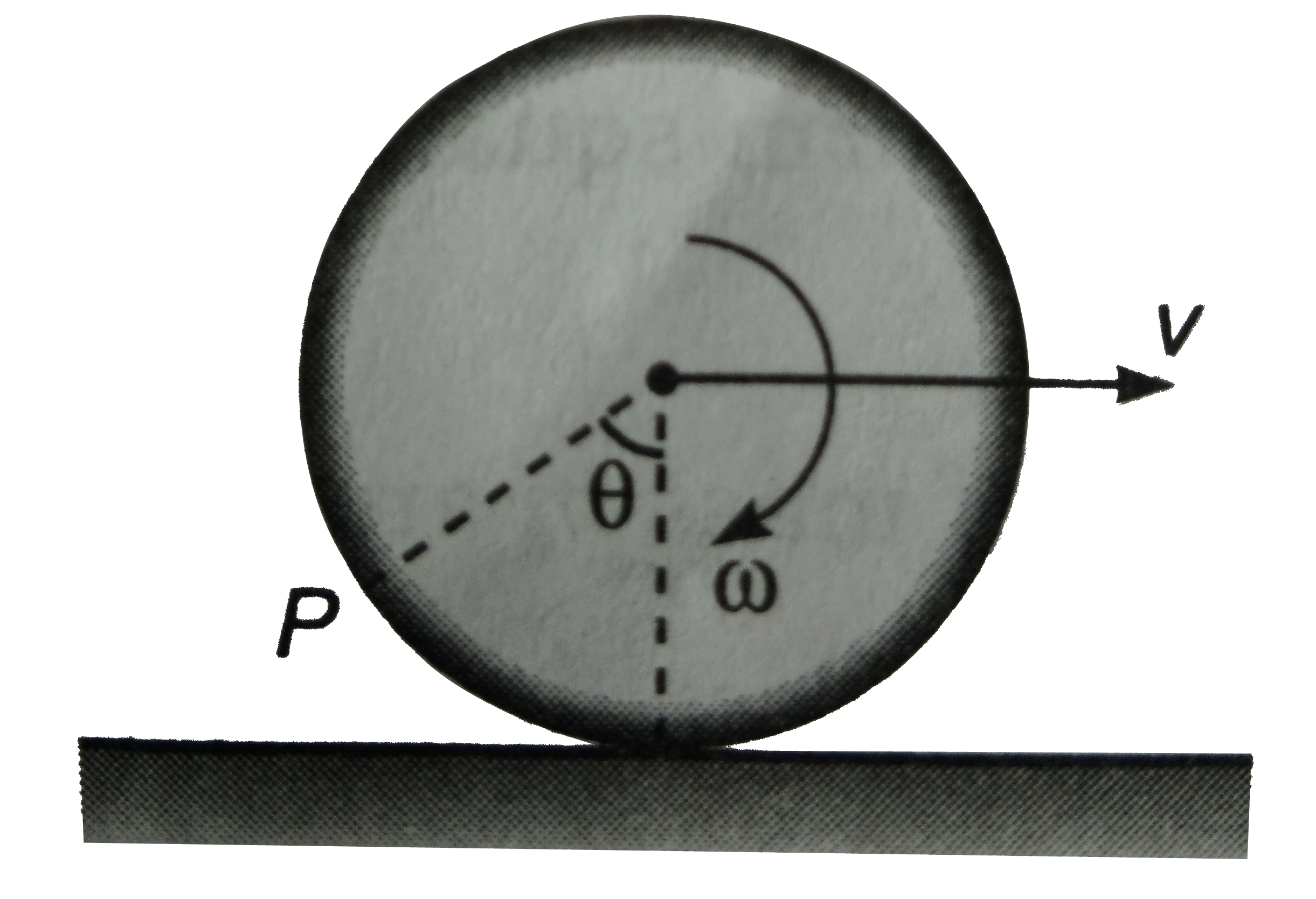
A ring of radius R rolls on a horizontal ground with linear speed v and angular speed ω. For what value of θ the velocity of point P is in vertical direction (v<Rω).
View SolutionA disc is in the condition of pure rolling on the horizontal surface. The velocity of center of mass isV0 If radius of disc is R then the speed of point P is (OP=R3)
View SolutionA circular disc of radius R rolls without slipping along the horizontal surface with constant velocity v0 . We consider a point A on the surface of the disc. Then, the acceleration of point A is
View SolutionA wheel of radius R=2m performs pure rolling on a rough horizontal surface with speed v=10 m/s . In the figure shown, angle θ is angular position of point P on wheel reaches the maximum height from ground. Find the value of secθ (take g=10m/s2).
View SolutionA disc of mass M and radius R rolls on a horizontal surface and then rolls up an inclined plane as shown in the figure. If the velocity of the disc is v, the height to which the disc will rise will be:

View SolutionFrom a uniform disc of radius R, an equilateral triangle of side √3R is cut as shown in the figure. The new position of centre of mass is :

View Solution
