A bimetalic strip is made of two strips A and B, having co-efficeint of linear expansion as αA and αB. If αA>αB which of the following describes the behavior fo the metallic strip when heated?
It will bend but will not elongate
It will bend the metal A s the outer side
It will bend with metal B as the outer side
It will not bend
To solve the problem regarding the behavior of a bimetallic strip made of two metals A and B when heated, we can follow these steps:
Step 1: Understand the Concept of Linear Expansion
When a material is heated, it expands. The amount of expansion depends on the coefficient of linear expansion (α) of the material. The formula for linear expansion is given by:
ΔL=L⋅α⋅ΔT
where:
- ΔL = change in length,
- L = original length,
- α = coefficient of linear expansion,
- ΔT = change in temperature.
Step 2: Identify the Coefficients of Linear Expansion
In this case, we have two metals:
- Metal A with coefficient of linear expansion αA,
- Metal B with coefficient of linear expansion αB.
According to the problem, it is given that:
αA>αB
Step 3: Calculate the Change in Length for Both Metals
When the bimetallic strip is heated, both metals will expand, but by different amounts due to their coefficients of linear expansion.
The change in length for metal A is:
ΔLA=L⋅αA⋅ΔT
The change in length for metal B is:
ΔLB=L⋅αB⋅ΔT
Step 4: Compare the Changes in Length
Since αA>αB, it follows that:
ΔLA>ΔLB
This means that metal A will expand more than metal B when heated.
Step 5: Analyze the Physical Behavior of the Bimetallic Strip
Since the two metals are bonded together at one end, they cannot expand freely. When heated, metal A (with greater expansion) will try to expand more than metal B. This will cause the bimetallic strip to bend.
Step 6: Determine the Direction of Bending
Given that metal A expands more, it will be on the outer side of the bend, while metal B, which expands less, will be on the inner side. Therefore, when the strip is heated, it will bend such that:
- Metal A is on the outer side,
- Metal B is on the inner side.
Conclusion
The correct description of the behavior of the bimetallic strip when heated is that it will bend with metal A on the outer side.
Final Answer
The bimetallic strip will bend with metal A on the outer side.
---
When a material is heated, it expands. The amount of expansion depends on the coefficient of linear expansion (α) of the material. The formula for linear expansion is given by:
ΔL=L⋅α⋅ΔT
where:
- ΔL = change in length,
- L = original length,
- α = coefficient of linear expansion,
- ΔT = change in temperature.
In this case, we have two metals:
- Metal A with coefficient of linear expansion αA,
- Metal B with coefficient of linear expansion αB.
αA>αB
When the bimetallic strip is heated, both metals will expand, but by different amounts due to their coefficients of linear expansion.
ΔLA=L⋅αA⋅ΔT
ΔLB=L⋅αB⋅ΔT
Since αA>αB, it follows that:
ΔLA>ΔLB
This means that metal A will expand more than metal B when heated.
Since the two metals are bonded together at one end, they cannot expand freely. When heated, metal A (with greater expansion) will try to expand more than metal B. This will cause the bimetallic strip to bend.
Given that metal A expands more, it will be on the outer side of the bend, while metal B, which expands less, will be on the inner side. Therefore, when the strip is heated, it will bend such that:
- Metal A is on the outer side,
- Metal B is on the inner side.
The correct description of the behavior of the bimetallic strip when heated is that it will bend with metal A on the outer side.
The bimetallic strip will bend with metal A on the outer side.
Topper's Solved these Questions
- HEAT AND THERMAL EXPANSIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - HEAT AND THERMAL EXPANSIONEXERCISE - NUMERICAL MCQs SINGLE OPTIONS CORRECT
81 Videos
- HEAT AND THERMAL EXPANSIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - HEAT AND THERMAL EXPANSIONEXERCISE - ADVANCE MCQs WITH ONE OR MORE OPTIONIS CORRECT
24 Videos
- HEAT AND THERMAL EXPANSIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - HEAT AND THERMAL EXPANSIONEXERCISE - DISCUSSION QUESTION
24 Videos
- GEOMETRICAL OPTICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - GEOMETRICAL OPTICSEXERCISE - Unsolved Numerical Problems
107 Videos
- HEAT TRANSFER BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - HEAT TRANSFER EXERCISE - Unsolved Numerical Problems for Preparation of NSEP,INPhO&IPhO
66 Videos
Similar Questions
A bimetallic strip is made up of two metals with different α
View SolutionTwo straight metallic strips each of thickness t and length l are rivetted together. Their coefficients of linear expansions areα1andα2. If they are heated through temperature ΔT, the bimetallic strip will bend to form an arc of radius
View Solution
Knowledge Check
A bimetallic is made of two strips A and B having coefficients of linear expansion α4andαB. If αA<αB, then on heating, the strip will
ABend with A on outer sideBBend with B on outer sideCNot bend at allDNone of the aboveA bimetallic is made of two strips A and B having coefficients of linear expansion α4andαB. If αA<αB, then on heating, the strip will
ABend with A on outer sideBBend with B on outer sideCNot bend at allDNone of the aboveWhen a strip made or iron (α1) and copper (α2),(α2>α1) is heated
Aits length does not changeBit gets twistedCit bends with iron on concave sideDit bends with iro on convex side
A bimetalis strip conists of two metakl strips with diffesrent coefficients of linear expansion α1 and α2 each of small thickness d and length L0 at T0. They are bonded together and, with a change in temperature De<AT, will curve in a circular arc, as shown in figure. Show that the radius of curvature R is given approximately be
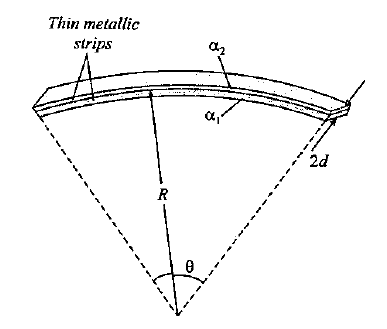
R=d(α2−α1)ΔT
View SolutionTwo mettalic strips each of length l0 and thickness d, temperature T0 are riveted together so that their ends coincide. One strip is maxe of a metal of coeficient of expansioin α1 and the other of a metal with a coefficient α2, where α2>α1. When this bimetallic strip is heated to a temperature T0+ΔT, find the radius of curvature R of the strip.
View SolutionTwo rods of length L1 and L2 are made of materials of coefficients of linear expansions α1 an α2 respectively such that L1α1=L2α2. The temperature of the rods is increased by ΔT and correspondingly the change in their respective lengths be ΔL1 and ΔL2
View SolutionA bimetallic strip is formed out of two identical strips one of copper and the other of brass. The co-efficients of linear expansion of the two metals are αC and αB. On heating, the the strip bends to form an are of radius of curvature R. Then R is
View SolutionSTATEMENT - 1 : A metallic rod placed upon smooth surface is heated. The strain produced is ZERO.
STATEMENT - 2 : Strain is non-zero only when stress is developed in the rod.
STATEMENT - 3 : Two metallic rods of length l1 and l2 and coefficient of linear expansion α1 and α2 are heated such that the difference of their length ramains same at ALL termperatures Then α1α2=l2l1
View Solution
