The heat (Q) supplied to a solid, which is otherwise thermally isolated from it surrounding, is plotted as a function of its absolute temperature, $θ$ . If is found that they are related by the equation $Q = a θ^{2} + b θ^{4}$ ( a, b are constants). The heat capacity of the solid is,

$a \frac{θ^{3}}{3} + b \frac{θ^{5}}{5}$

$a θ + b θ^{3}$

$a \frac{θ}{3} + b \frac{θ^{5}}{5}$

$2 a θ + 4 b θ^{3}$

Video Solution

Text Solution

Generated By DoubtnutGPT

To find the heat capacity of the solid given the relation $Q = a θ^{2} + b θ^{4}$ , we can follow these steps:
1. Understand the Relationship: We start with the equation given in the problem:
$Q = a θ^{2} + b θ^{4}$
Here, $Q$ is the heat supplied, $θ$ is the absolute temperature, and $a$ and $b$ are constants.
2. Define Heat Capacity: The heat capacity $C$ of a substance is defined as the amount of heat required to change its temperature by one degree. Mathematically, it can be expressed as:
$C = \frac{d Q}{d θ}$
This means we need to differentiate $Q$ with respect to $θ$ .
3. Differentiate $Q$ : We will differentiate the expression for $Q$ :
$\frac{d Q}{d θ} = \frac{d}{d θ} (a θ^{2} + b θ^{4})$
Using the power rule of differentiation, we get:
$\frac{d Q}{d θ} = 2 a θ + 4 b θ^{3}$
4. Final Expression for Heat Capacity: Thus, the heat capacity $C$ of the solid is:
$C = 2 a θ + 4 b θ^{3}$
Conclusion:
The heat capacity of the solid is given by:
$C = 2 a θ + 4 b θ^{3}$

Updated on:7/8/2024

Class 12 PHYSICS HEAT AND THERMAL EXPANSION

Topper's Solved these Questions

Knowledge Check

Question 1 - Select One
Curved surface of a uniform rod is isolated from surrounding. Ends of the rod are maintained at temperatures $T_{1}$ and $T_{2} (T_{1} > T_{2})$ for a long time. At an instant, temperature $T_{1}$ starts to decrease at a constant and slow rate. If thermal capacity of material of the rod is considered, then which of thefollowing statements is/are correct ?
A) At an instant,rate of heat flow near the hotter end is equal to that near the other end
BRate of heat flow through the rod starts to decrease near the hotter end and remains constant near the other end
CRate of heat flow is maximum at mid section of the rod
DNone of these
Question 2 - Select One
A substance is in the solid from at $0^{\circ} C$ . The amount of heat added to this substance and its temperature is plotted in the graph . The specific heat capacity of the solid substance is $0.5 cal / g^{\circ} C$ .

Specific heat capacity in the liquid state is -
A $\frac{5}{27} cal / g^{\circ} C$
B $\frac{5}{27} cal / g K$
C $\frac{10}{27} cal / g^{\circ} C$
DCan't say
Question 3 - Select One
Figure shows an electrical calorimeter to determine specific heat capacity of an unknown liquid, First of all, the mass of empty calorimeter (a copper container) is measured and suppose it is $m_{1}$ . Then the unknown liquid is poured in it. Now the combined mass of calorimeter+liquid system is measured and let it be $m_{2}$ . So the mass of liquid is $(m_{2} - m_{1})$ . Initially both were at room temperature ( $θ_{0}$ ).
Now a heater is immeresed in if for time interval $t$ . The voltage drop across the heater is $V$ and current passing through it is $I$ . Due to heat supplied, the temperature of both the liquid and calorimeter will rise simultaneously. After $t sec$ , heater was switched off, and final temperature is $θ_{r}$ . If there is no heat loss to surroundings. Heat supplied by the heater=Heat absorbed by the liquid+heat absorbed by the calorimeter $(V I) t = (m_{2} - m_{1}) S_{1} (θ_{f} - θ_{0}) + m_{1} S_{c} (θ_{f} - θ_{0})$
The specific heat of the liquid $S_{1} = \frac{\frac{(V I) t}{θ_{f} - θ_{0}} - m_{1} S_{c}}{(m_{2} - m_{1})}$

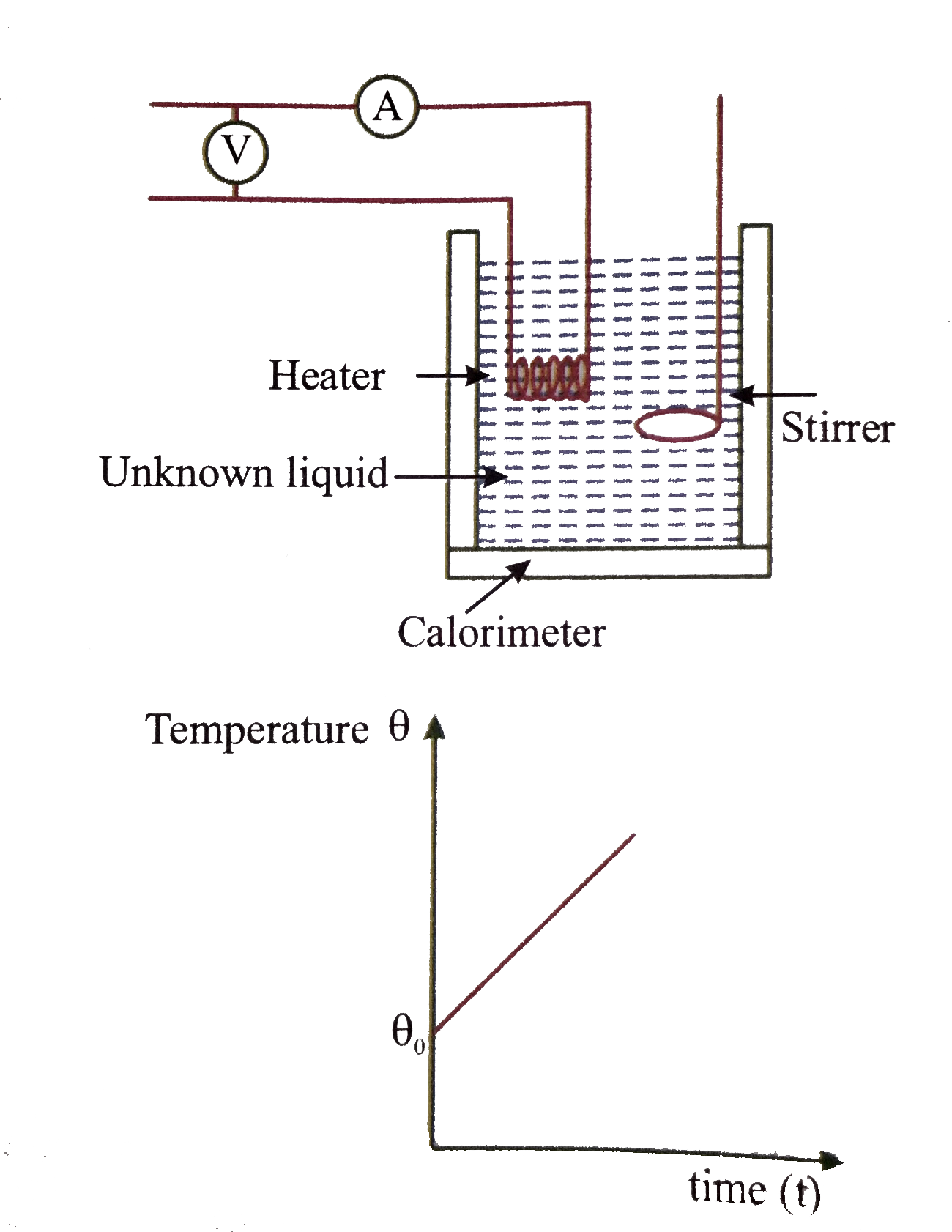
Radiation correction: There can be heat loss to environment. To compensate this loss, a correction is introduced.
Let the heater was on for $t sec$ , and then it is switched off. Now the temperature of the mixture falls due to heat loss to environment. The temperature of the mixture is measured $t / 2 sec$ . after switching off. Let the fall in temperature during this time is $ɛ$
Now the corrected final temperature is taken as $θ_{f} = θ_{f} + ɛ$
If mass and specific heat capacity of calorimeter is negligible, what would be maximum permissible error in $S_{l}$ . Use the date mentioned below.
$m_{1} \to$ , $S_{l} \to 0$ , $m_{2} = 1.00 k g$ ,
$V = 10.0 V$ , $I = 10.0 A$ ,
$t = 1.00 \times 10^{2} sec$ , $θ_{0} = 15^{\circ} C$ ,
Corrected $θ_{1} = 65^{\circ} C$
A $4 %$
B $5 %$
C $8 %$
D $12 %$

PHYSICS GALAXY - ASHISH ARORA-HEAT AND THERMAL EXPANSION-CONCEPTUAL MCQs SINGLE OPTION CORRECT

Home
Ask Doubt
Profile

The heat (Q) supplied to a solid, which is otherwise thermally isolated from it surrounding, is plotted as a function of its absolute temperature, θ. If is found that they are related by the equationQ=aθ2+bθ4 ( a, b are constants). The heat capacity of the solid is,

Topper's Solved these Questions

Similar Questions

Knowledge Check

A substance is in the solid from at 0∘C. The amount of heat added to this substance and its temperature is plotted in the graph . The specific heat capacity of the solid substance is 0.5cal/g∘C. Specific heat capacity in the liquid state is -

PHYSICS GALAXY - ASHISH ARORA-HEAT AND THERMAL EXPANSION-CONCEPTUAL MCQs SINGLE OPTION CORRECT

The heat (Q) supplied to a solid, which is otherwise thermally isolated from it surrounding, is plotted as a function of its absolute temperature, $θ$ . If is found that they are related by the equation $Q = a θ^{2} + b θ^{4}$ ( a, b are constants). The heat capacity of the solid is,

A substance is in the solid from at $0^{\circ} C$ . The amount of heat added to this substance and its temperature is plotted in the graph . The specific heat capacity of the solid substance is $0.5 cal / g^{\circ} C$ .

Specific heat capacity in the liquid state is -