A block A of mass 2kg rests on another block B of mass 8kg which rests on a horizontal floor. The coefficient of friction between A and B is 0.2 while that between B and floor is 0.5.When a horizontal floor F of 25N is applied on the block B the force of friction between A and B is
(a)3N
(b)4N
(c)2N
(d)zero
The correct Answer is:D
To solve the problem, we need to determine the force of friction between block A and block B when a horizontal force of 25 N is applied to block B. Here’s a step-by-step breakdown of the solution:
Step 1: Identify the masses and coefficients of friction
- Mass of block A (m_A) = 2 kg
- Mass of block B (m_B) = 8 kg
- Coefficient of friction between A and B (μ_AB) = 0.2
- Coefficient of friction between B and the floor (μ_BF) = 0.5
Step 2: Calculate the normal force acting on block B
The normal force (N) acting on block B is the combined weight of both blocks A and B.
N=(mA+mB)⋅g
Where g is the acceleration due to gravity, approximately 10m/s2.
Substituting the values:
N=(2kg+8kg)⋅10m/s2=10kg⋅10m/s2=100N
Step 3: Calculate the maximum frictional force between B and the floor
The maximum frictional force (F_friction_BF) that can act between block B and the floor is given by:
Ffriction\_BF=μBF⋅N
Substituting the values:
Ffriction\_BF=0.5⋅100N=50N
Step 4: Determine the applied force and compare it with the frictional force
An external force of 25 N is applied to block B. The frictional force between block B and the floor can resist up to 50 N. Since the applied force (25 N) is less than the maximum frictional force (50 N), block B will not move.
Step 5: Analyze the effect on block A
Since block B does not move, block A will also not move relative to block B. Therefore, the force of friction between block A and block B will be equal to the force required to keep block A stationary with respect to block B.
Step 6: Calculate the force of friction between A and B
Since block A is at rest relative to block B, the force of friction between them must be equal to the force that would be required to keep block A from sliding off block B. However, since block B is not moving, the frictional force between A and B is effectively zero.
Thus, the force of friction between block A and block B is:
Ffriction\_AB=0N
Final Answer
The force of friction between block A and block B is 0 N.
---
- Mass of block A (m_A) = 2 kg
- Mass of block B (m_B) = 8 kg
- Coefficient of friction between A and B (μ_AB) = 0.2
- Coefficient of friction between B and the floor (μ_BF) = 0.5
The normal force (N) acting on block B is the combined weight of both blocks A and B.
N=(mA+mB)⋅g
Where g is the acceleration due to gravity, approximately 10m/s2.
N=(2kg+8kg)⋅10m/s2=10kg⋅10m/s2=100N
The maximum frictional force (F_friction_BF) that can act between block B and the floor is given by:
Ffriction\_BF=μBF⋅N
Substituting the values:
Ffriction\_BF=0.5⋅100N=50N
An external force of 25 N is applied to block B. The frictional force between block B and the floor can resist up to 50 N. Since the applied force (25 N) is less than the maximum frictional force (50 N), block B will not move.
Since block B does not move, block A will also not move relative to block B. Therefore, the force of friction between block A and block B will be equal to the force required to keep block A stationary with respect to block B.
Since block A is at rest relative to block B, the force of friction between them must be equal to the force that would be required to keep block A from sliding off block B. However, since block B is not moving, the frictional force between A and B is effectively zero.
Ffriction\_AB=0N
The force of friction between block A and block B is 0 N.
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Objective Question
32 Videos
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Comprehension
9 Videos
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Assertion And Reason
28 Videos
- KINEMATICS 1BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE
15 Videos
- LAWS OF THERMODYNAMICSBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 2 Subjective
18 Videos
Similar Questions
A block A of mass 2kg is placed over smooth block B of mass 4kg which is placed over a smooth horizontal floor The coefficient of friction between A and B is 0.4 when a horizontal forces of magnitude 10N is applied on A the acceleration of block of A and B are

View SolutionA block of mass 2 kg is at rest on a floor . The coefficient of static friction between block and the floor is 0.54. A horizonatl force of 2.8 N is applied to the block . What should be the frictional force between the block and the floor ? ( take , g=10m/s2)
View SolutionA block A of mass m kg lies on a block B of mass m kg. B in turn lies on smooth horizontal plane. The coefficient of friction between A and B is μ. Both the blocks are initially at rest. A horizontal force F is applied to lower block B at t = 0 till the lower block B undergoes a displacement of magnitude L. Match the statements in Table-1 with the results in Table-2.

View SolutionA small block of mass 20kg rests on a bigger block of mass 30kg, which lies on a smooth horizontal plane. Initially the whole system is at rest. The coefficient of friction between the blocks is 0.5. The horizontal force F=50N is applied on the lower block.
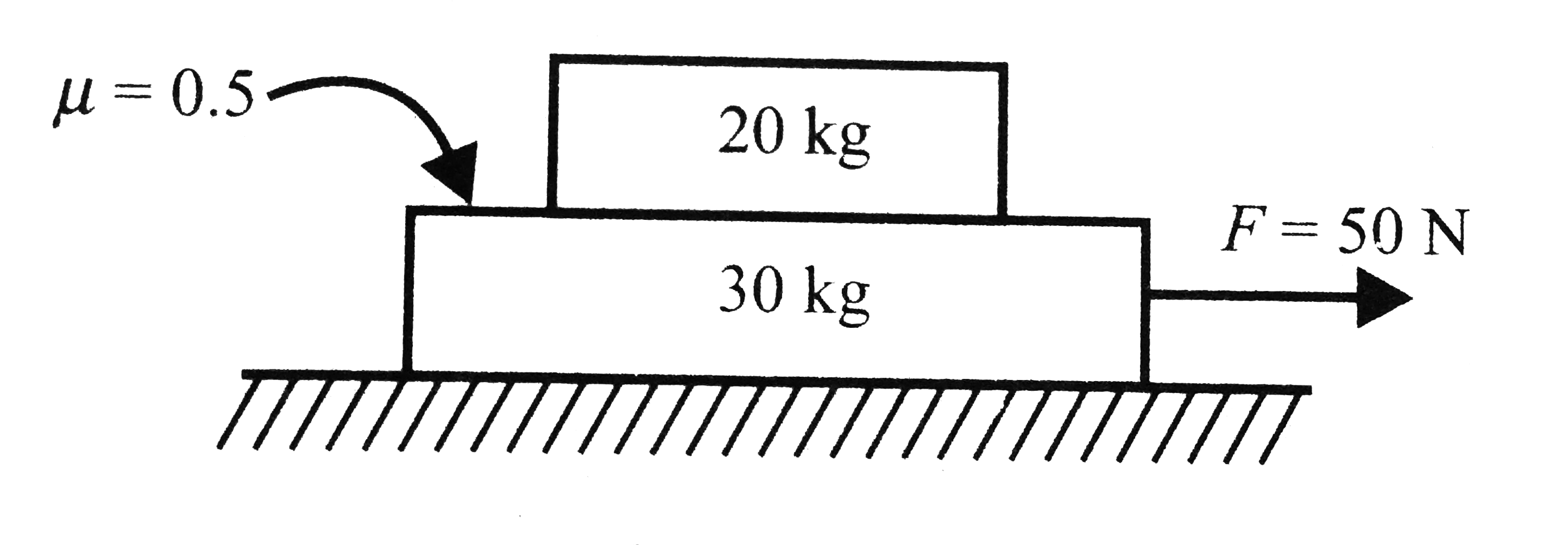
a. Find the work done by fricitonal force on upper block and on the lower block in t=2s.
b. Is the magnitude of work done by the frictional force on upper and lower blocks same?
c. Is the work done by the frictional force on the upper block converted to heat or mechanical energy or both?
View SolutionBlock A of mass m rests on the plank B of mass 3m which is free to slide on a frictionless horizo-ntal surface. The coefficient of friction between the block and plank is 0.2. If a horizontal force of magnitude 2 mg is applied to the plank B, the acceleration of A relative to the plank and relative to the ground respectively, are:

View SolutionBlock A of mass 2kg is placed over a block B of mass 8kg . The combination is placed on a rough horizontal surface. If g=10ms−2 , coefficient of friction between B and floor =0.5 , coefficient of friction between B and floor =0.5 , coefficient of friction between A and B=0.4 and a horizontal force of 10N is applied on 8kg block, then the force of friction between A and B is.

View SolutionBlock A of mass 2kg is placed over a block B of mass 8kg . The combination is placed on a rough horizontal surface. If g=10ms−2 , coefficient of friction between B and floor =0.5 , coefficient of friction between B and floor =0.5 , coefficient of friction between A and B=0.4 and a horizontal force of 10N is applied on 8kg block, then the force of friction between A and B is.

View SolutionA block A with mass 100kg is resting on another block B of mass 200kg. As shown in figure a horizontal rope tied to a wall hold it. The coefficient of friction between A and B is 0.2 while coefficient of friction between B and the ground is 0.3 . the minimum required force F to start moving B will be.

View SolutionA block A with mass 100kg is resting on another block B of mass 200kg. As shown in figure a horizontal rope tied to a wall hold it. The coefficient of friction between A and B is 0.2 while coefficient of friction between B and the ground is 0.3 . the minimum required force F to start moving B will be.

View SolutionA block A with mass 100kg is resting on another block B of mass 200kg. As shown in figure a horizontal rope tied to a wall hold it. The coefficient of friction between A and B is 0.2 while coefficient of friction between B and the ground is 0.3 . the minimum required force F to start moving B will be.

View Solution