A block A of mass m is tied to a fixed point C on a horizontal table through a string passing round a mass less smooth pulley B.A force F is applied by the pulley B as shown in
(b) Find the accelerations of the pulley and mass A.
The correct Answer is:aA=F/2mandaB=F/4m
To solve the problem of finding the accelerations of the pulley B and mass A, we can follow these steps:
Step 1: Identify the Forces Acting on the Pulley
The pulley B is subjected to:
- An applied force F in the forward direction.
- Two tensions T acting backward due to the string on both sides of the pulley.
Step 2: Write the Equation of Motion for the Pulley
Since the pulley is massless, we can apply Newton's second law:
F−2T=0
This implies:
F=2T
From this, we can express the tension T:
T=F2
Step 3: Analyze the Forces Acting on Mass A
For mass A, the only force acting on it is the tension T in the string. According to Newton's second law:
T=m⋅aA
where aA is the acceleration of mass A. Substituting the expression for T:
F2=m⋅aA
Thus, we can solve for the acceleration of mass A:
aA=F2m
Step 4: Relate the Accelerations of the Pulley and Mass A
Next, we need to relate the acceleration of the pulley aB to the acceleration of mass A. When the pulley moves a distance x forward, the length of the string on either side of the pulley changes. The relationship can be established as:
If the pulley moves forward by x, then mass A moves backward by 2x.
Thus, the acceleration of the pulley aB is half of the acceleration of mass A:
aB=12aA
Step 5: Substitute the Expression for aA
Substituting the expression for aA into the equation for aB:
aB=12(F2m)=F4m
Final Results
Thus, the accelerations of the pulley and mass A are:
- Acceleration of mass A:
aA=F2m
- Acceleration of pulley B:
aB=F4m
The pulley B is subjected to:
- An applied force F in the forward direction.
- Two tensions T acting backward due to the string on both sides of the pulley.
Since the pulley is massless, we can apply Newton's second law:
F−2T=0
This implies:
F=2T
From this, we can express the tension T:
T=F2
For mass A, the only force acting on it is the tension T in the string. According to Newton's second law:
T=m⋅aA
where aA is the acceleration of mass A. Substituting the expression for T:
F2=m⋅aA
Thus, we can solve for the acceleration of mass A:
aA=F2m
Next, we need to relate the acceleration of the pulley aB to the acceleration of mass A. When the pulley moves a distance x forward, the length of the string on either side of the pulley changes. The relationship can be established as:
If the pulley moves forward by x, then mass A moves backward by 2x.
Thus, the acceleration of the pulley aB is half of the acceleration of mass A:
aB=12aA
Substituting the expression for aA into the equation for aB:
aB=12(F2m)=F4m
Thus, the accelerations of the pulley and mass A are:
- Acceleration of mass A:
aA=F2m
- Acceleration of pulley B:
aB=F4m
Topper's Solved these Questions
- FORCE AND NEWTONS LAWS OF MOTIONBOOK - GRB PUBLICATIONCHAPTER - FORCE AND NEWTONS LAWS OF MOTIONEXERCISE - Objective Questions
134 Videos
- FORCE AND NEWTONS LAWS OF MOTIONBOOK - GRB PUBLICATIONCHAPTER - FORCE AND NEWTONS LAWS OF MOTIONEXERCISE - More than one choice is correct
15 Videos
- FORCE AND NEWTONS LAWS OF MOTIONBOOK - GRB PUBLICATIONCHAPTER - FORCE AND NEWTONS LAWS OF MOTIONEXERCISE - Problem
33 Videos
- BASIC MATHEMATICSBOOK - GRB PUBLICATIONCHAPTER - BASIC MATHEMATICSEXERCISE - Problems For Practice
35 Videos
- FRICTION AND CIRCULAR MOTION BOOK - GRB PUBLICATIONCHAPTER - FRICTION AND CIRCULAR MOTION EXERCISE - Comprehension type
11 Videos
Similar Questions
A block A of mass m is tied to a fixed point C on a horizontal table through a string passing round a massless smooth pulley B. A force F is applied by the experimenter to the pulley. Show tht if the pulley is displaced by a distance x theblock will be displaced by 2x. Find the acceleration of the block and the pulley.

View SolutionA block of mass 20 kg is set into motion on a frictionless horizontal surface with the help of massless smooth pulley and rope as shown in the figure. Find the acceleration of the pulley
_PHY_E05_192_Q05.png)
View Solution
Knowledge Check
A block of mass M is pulled on a smooth horizontal table by a string making an angle θ with the horizontal as shown in figure. If the acceleration of the block is a find the force applied by the string and by the table N on the block.
 AT=Matanθ , N=(Mg−Matanθ)BT=Mgcosθ , N=(Mg−Matanθ)CT=Macosθ , N=(Mg−Macosθ)DT=Macosθ , N=(Mg−Matanθ)
AT=Matanθ , N=(Mg−Matanθ)BT=Mgcosθ , N=(Mg−Matanθ)CT=Macosθ , N=(Mg−Macosθ)DT=Macosθ , N=(Mg−Matanθ)A block of mass m is attached at the end of an inextensible string which is wound over a rough pulley of mass M and radius R. Assume the string does not slide over the pulley. Find the acceleration of the block when released.
Amg2m+MB2mgm+MCmgm+MD2mg2m+M
Two blocks A and B of masses m and M are attached with ideal string and pulley, and placed on smooth horizontal surface. Force F is applied horizontally as shown in figure. Find the ratio of the acceleration of A to that of B.

View SolutionA block of mass M is placed on a horizontal surface. It is tied with an inextensible string that passes through ideal pulleys. A mass m is connected to the pulley as shown. For what value of m, the block M will accelerate towards the fixed pulley ?
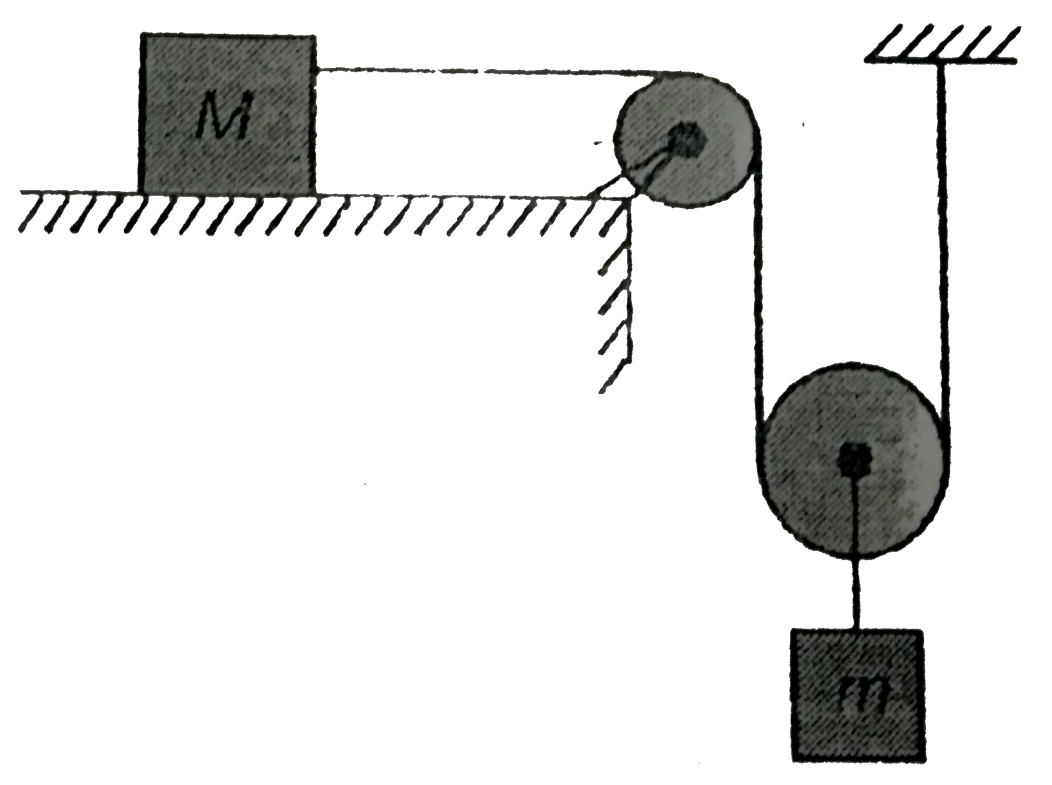
View SolutionIn the arrangement shown, the pulleys and the strings are ideal.The acceleration of the block B is
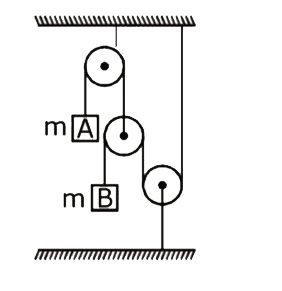
View SolutionFigure shows two blocks of mass m and m connected by a string passing over a pulley. The horizontal table over which the mass m slides is smooth. The pulley (uniform disc) has mass m and it can freely rotate about this axis. Find the acceleration of the mass m assuming that the string does not slip on the pulley.
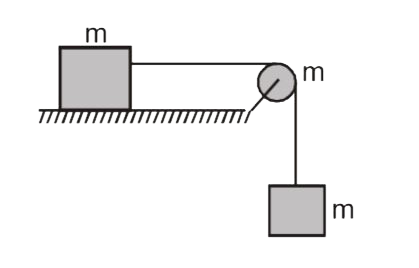
View SolutionTwo blocks A and B of equal masses are attached to a string passing over a smooth pulley fixed to a wedge as shown in figure. Find the magnitude of acceleration of centre of mass of the two blocks when they are released from rest. Neglect friction.

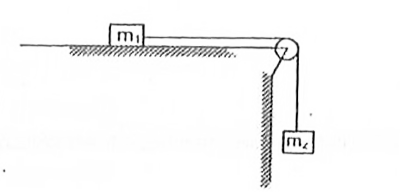
View SolutionA block of mass m1=2 kg is kept on a smooth horizontal table. Another block of mass m2=1 kg is connected to m1 by a light inextensible string passing over a smooth pulley as shown in the figure. If the blocks are released, what will be the (a) acceleration of each block (b) tension in the string?
View Solution
