Question

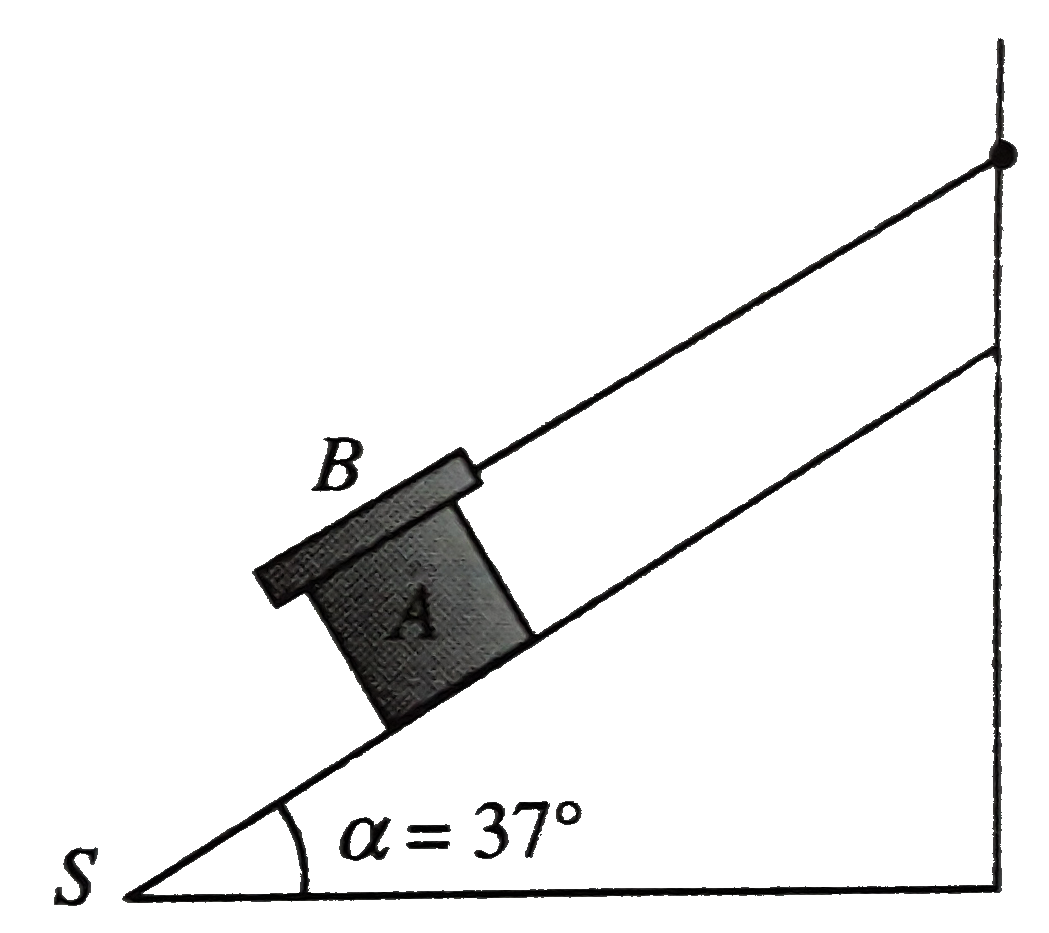
A block A of weight $W$ slide down an inclined plane S of slope ${37}^{\circ }$at a constant velocity, while the plank B also of weight $W$ rests on top of $A$. The plank B is attached by a cord to the top of plane .The coefficient of kinetic friction $\mu$ is the same between the surface A and B and between S and A Determine the value of $1/\mu$

Answer

4

Explanation

Since A tends to slip down ,frictional force act on it from both sides up the plane
Let N be the reaction of the plank on A and N be the mutual normal action - rection between A and B
From the free-body diagram ofA
`N= mg cos alpha = N and mg sin alpha = mu (N + N)`
From the free-body diagram of B

`N = mg cos alpha`
`mg sin alpha = mu N = T`
`:. 2 mg cos alpha = N `
`and mg sin alpha = mu(2mg cos alpha + mg cos alpha)`
`or mu = (1)/(3) tan alpha = (1)/(3) xx (3)/(4) = 0.25 or (1)/(m) = 4`