A block can slide on a smooth inclined plane of inclination θ kept on the floor of a lift. When the lift is descending with a retardation a , the acceleration of the block relative to the incline is
(g+a)sinθ
(g−a)
gsinθ
(g−a)sinθ
The correct Answer is:A
To find the acceleration of the block relative to the inclined plane when the lift is descending with a retardation a, we will follow these steps:
Step 1: Understand the Forces Acting on the Block
When the lift is descending with retardation a, we can consider the effective acceleration acting on the block due to gravity and the retardation of the lift. The gravitational force acting on the block is mg (where m is the mass of the block and g is the acceleration due to gravity).
Step 2: Define the Effective Acceleration
Since the lift is descending with retardation a, we can consider this as an upward acceleration of a for the block relative to the lift. Therefore, the effective acceleration acting on the block can be expressed as:
geffective=g+a
This is because the block experiences an additional upward pseudo force due to the retardation of the lift.
Step 3: Resolve Forces Along the Incline
The block is on an inclined plane with an angle θ. The component of the effective gravitational force acting down the incline can be calculated using:
Fdown incline=(g+a)⋅sin(θ)
This is the force that causes the block to accelerate down the incline.
Step 4: Apply Newton's Second Law
According to Newton's second law, the net force acting on the block along the incline is equal to the mass of the block multiplied by its acceleration relative to the incline:
F=m⋅arelative
Substituting the expression for the force down the incline, we have:
m⋅(g+a)⋅sin(θ)=m⋅arelative
Step 5: Solve for the Acceleration of the Block Relative to the Incline
We can cancel the mass m from both sides of the equation (assuming m≠0):
(g+a)⋅sin(θ)=arelative
Thus, the acceleration of the block relative to the incline is given by:
arelative=(g+a)⋅sin(θ)
Final Answer
The acceleration of the block relative to the incline is:
arelative=(g+a)⋅sin(θ)
When the lift is descending with retardation a, we can consider the effective acceleration acting on the block due to gravity and the retardation of the lift. The gravitational force acting on the block is mg (where m is the mass of the block and g is the acceleration due to gravity).
Since the lift is descending with retardation a, we can consider this as an upward acceleration of a for the block relative to the lift. Therefore, the effective acceleration acting on the block can be expressed as:
geffective=g+a
This is because the block experiences an additional upward pseudo force due to the retardation of the lift.
The block is on an inclined plane with an angle θ. The component of the effective gravitational force acting down the incline can be calculated using:
Fdown incline=(g+a)⋅sin(θ)
This is the force that causes the block to accelerate down the incline.
According to Newton's second law, the net force acting on the block along the incline is equal to the mass of the block multiplied by its acceleration relative to the incline:
F=m⋅arelative
Substituting the expression for the force down the incline, we have:
m⋅(g+a)⋅sin(θ)=m⋅arelative
We can cancel the mass m from both sides of the equation (assuming m≠0):
(g+a)⋅sin(θ)=arelative
Thus, the acceleration of the block relative to the incline is given by:
arelative=(g+a)⋅sin(θ)
The acceleration of the block relative to the incline is:
arelative=(g+a)⋅sin(θ)
Topper's Solved these Questions
- NEWTONS LAWS OF MOTIONBOOK - ERRORLESS CHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Assertion & Reason
25 Videos
- MOTION IN TWO DIMENSIONBOOK - ERRORLESS CHAPTER - MOTION IN TWO DIMENSIONEXERCISE - Exercise
319 Videos
- ROTATIONAL MOTIONBOOK - ERRORLESS CHAPTER - ROTATIONAL MOTIONEXERCISE - Practice Problems (Problems based on motion of connected mass)
10 Videos
Similar Questions
A block is released on an smooth inclined plane of inclination θ. After how much time it reaches to the bottom of the plane?

View SolutionA block of mass m is placed on a rough inclined plane of inclination θ kept on the floor of the lift. The coefficient of friction between the block and the inclined plane is μ. With what acceleration will the block slide down the inclined plane when the lift falls freely ?
View Solution
Knowledge Check
A block can slide on a smooth inclined plane of inclination θ kept on the floor of a lift. When the lift is descending with a retardation a , the acceleration of the block relative to the incline is
AThe acceleration of block relative to inclined is (g−a)sinθBThe normal force on block by the incline is m(g+a)cosθCThe acceleration of block relative to ground is gDThe acceleration of block relative to incline is (g+a)sinθThe acceleration of 10kg block on the inclined plane is
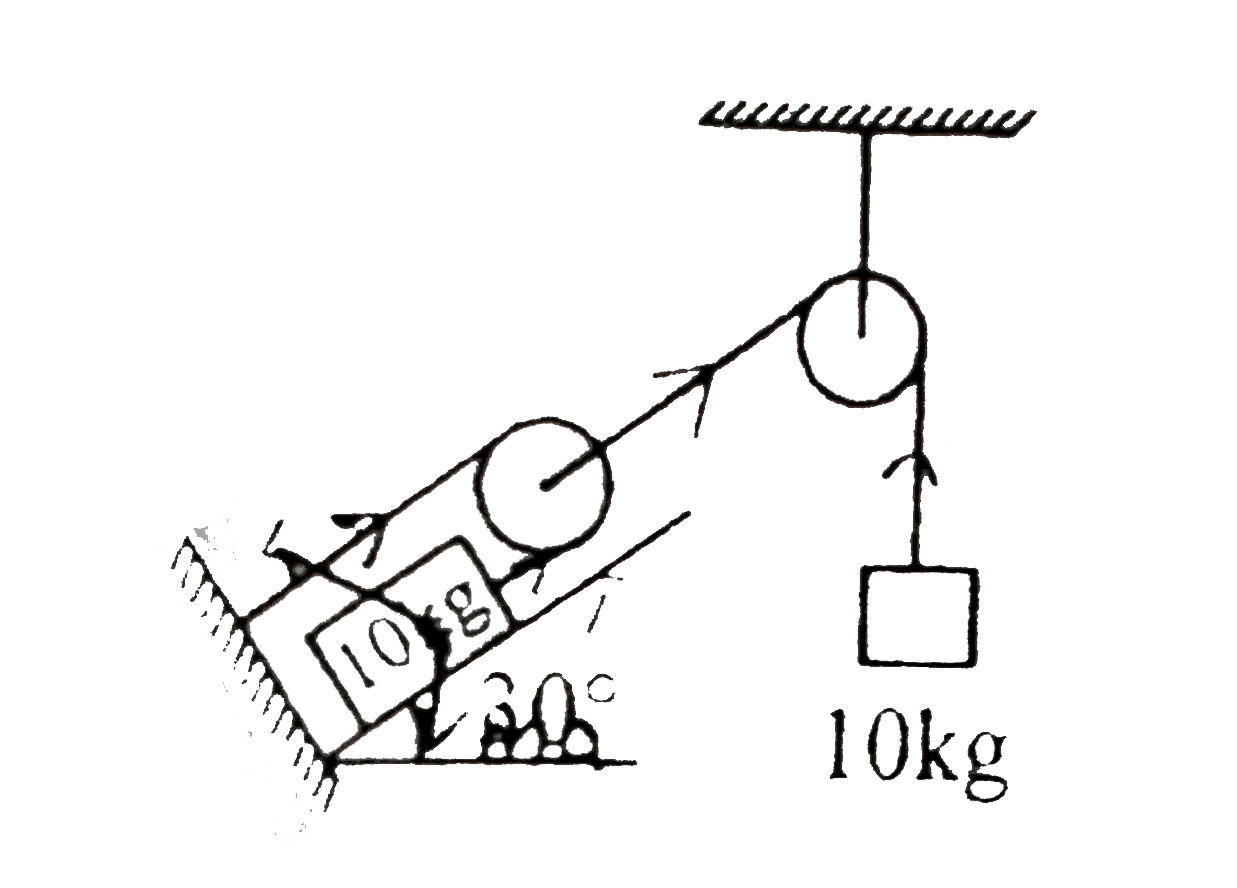 AzeroB4m/s2C6m/s2DNone of these
AzeroB4m/s2C6m/s2DNone of theseA block of mas m begins to slide down on an inclined plane of inclination θ. The force of friction will be
AmgBmgcosθCmgsinθDmgtanθ
A block is kept on a smooth inclined plane of angle of inclination θ that moves wuth a contact acceleration so that the block does not slide relative to the inclined plane. If the inclined plane stops the normal contact force offered by the plane on the block changes by a factor
View SolutionA block of mass m is placed on a smooth inclined plane of inclination θ with the horizontal. The force exerted by the plane on the block has a magnitude
View SolutionA small block of mass 2kg is kept on a rough inclined surface of inclination θ=30∘ fixed in a lift. The lift goes up with a uniform speed of 1ms−1 and the block does not slide relative to the inclined surface. The work done by the force of friction on the block in a time interval of 2s is
View SolutionA body of mass m is placed over a smooth inclined plane of inclination θ, which is placed over a lift which is moving up with an acceleration a0 . Base length of the inclined plane is L. Calculate the velocity of the block with respect to lift at the bottom, if it is allowed to slide down from the top of the plane from rest :-
View SolutionA body of mass m is placed over a smooth inclined plane of inclination theta. Which iis placed over a lift which is moving up with an acceleration a0 . Base length o f the inclined plane is L . Calculate the velocity of the block with respect to lift at the bottom, if it is allowed to slide down from the top o fthe plane from rest.
View Solution
