A block has a L shaped stand fixed to it. Mass of the block with the stand is M. At the free end of the stand there is a spring which carries a ball of mass m. With the spring in its natural length, the ball is released. It begins to oscillate and the stand is tall enough so that the ball does not hit the block.
(a) Find maximum value of mass (m) of the ball for which the block will not lose contact with the ground?
(b) If the stand is not tall enough and the ball makes elastic impact with the block, will your answer to part (a) change?

The correct Answer is:For both (a) and (b) the block will not lose contact with the ground for any value of m.
Step by step video, text & image solution for A block has a L shaped stand fixed to it. Mass of the block with the stand is M. At the free end of the stand there is a spring which carries a ball of mass m. With the spring in its natural length, the ball is released. It begins to oscillate and the stand is tall enough so that the ball does not hit the block. (a) Find maximum value of mass (m) of the ball for which the block will not lose contact with the ground? (b) If the stand is not tall enough and the ball makes elastic impact with the block, will your answer to part (a) change? by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBook:ARIHANTChapter:SIMPLE HARMONIC MOTIONExercise:Level 3
Explore 9 Videos
- SIMPLE HARMONIC MOTIONBook:ARIHANTChapter:SIMPLE HARMONIC MOTIONExercise:Level 3
Explore 9 Videos
- ROTATIONAL MOTIONBook:ARIHANTChapter:ROTATIONAL MOTIONExercise:PHYSICS
Explore 159 Videos
- SURFACE TENSIONBook:ARIHANTChapter:SURFACE TENSIONExercise:Surface tension
Explore 33 Videos
Similar Questions
Knowledge Check
Two blocks are connected to the two free ends of a spring of spring constant K . Both the blocks are moved apart to extend the psring beyond its natural length and then released . In subsequent motion
AAccelerations of both the objects are equal and opposite of each other .BVelocities of both the bjects are equal and opposite of each other .CForces acting on both the objects are equal and opposite of each otherDLinear momenta of both the objects are equal and opposite of each other .A block of mass m is attached to a spring of force constant k whose other end is fixed to a horizontal surface. Initially the spring is in its natural length and the block is released from rest. The average force acting on the surface by the spring till the instant when the block has zero acceleration for the first time is
 AmgπB2mgπC3mgπD4mgπ
AmgπB2mgπC3mgπD4mgπA block of mass 'm' is attached to a spring in natural length of spring constant 'k'. The other end A of the spring is moved with a constat velocity v away from the block . Find the maximum extension in the spring.
 A14√mv2kB√mv2kC12√mv2kD2√mv2k
A14√mv2kB√mv2kC12√mv2kD2√mv2k
All surfaces are smooth. The ball of mass m is released from A. Find the distance travelled by the block of mass M.
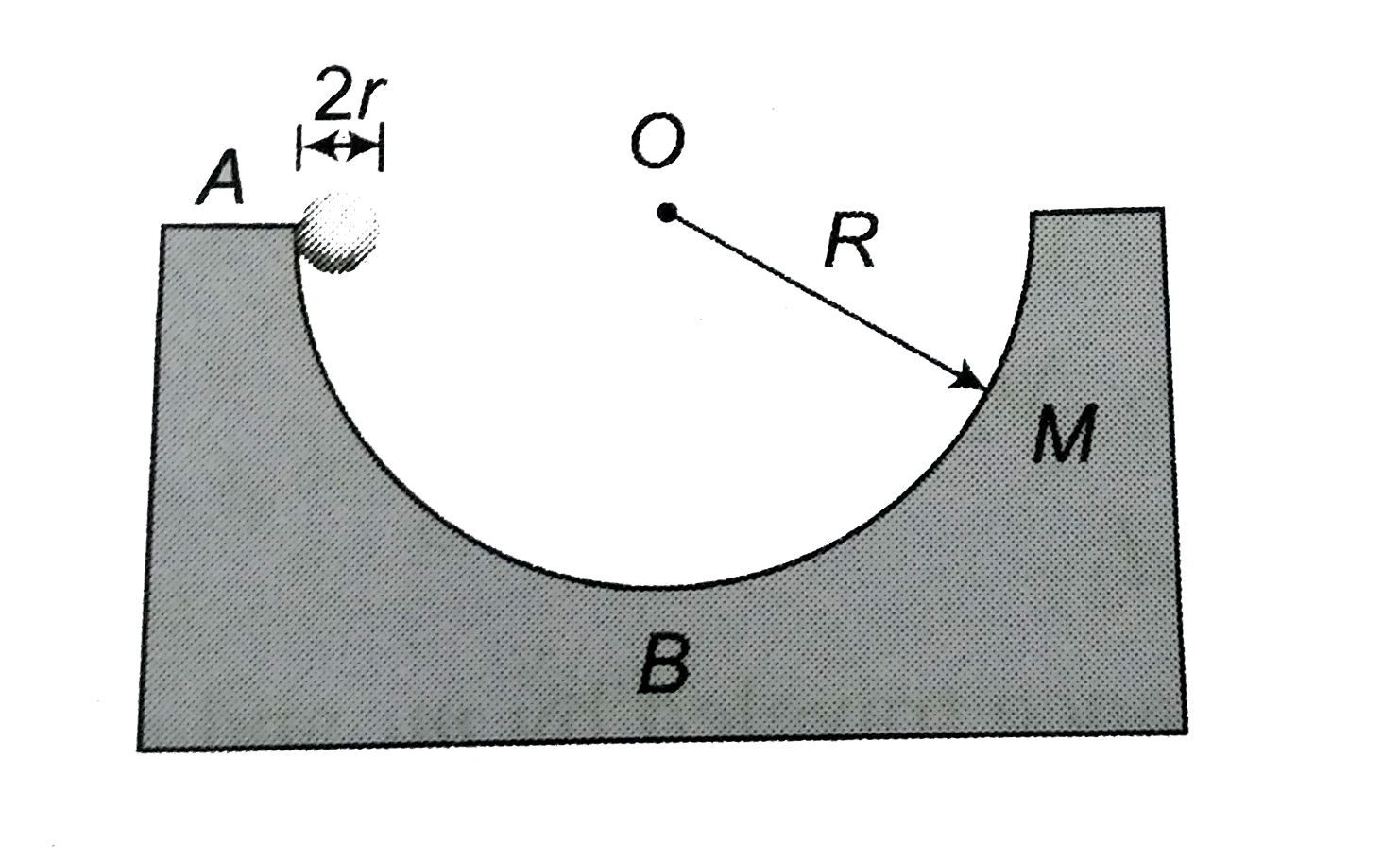
View Solution
A block of mass m is pushed against a spring of spring constant k fixed at one end to a wall.The block can slide on a frictionless table as shown in the figure. The natural length of the spring is L0 and it is compressed to one fourth of natural length and the block is released.Find its velocity as a function of its distance (x) from the wall and maximum velocity of the block. The block is not attached to the spring.
View SolutionIn the figure shown a block of masss m is atteched at ends of two spring The other ends of the spring are fixed The mass m is released in the vertical plane when the spring are released The velocity of the block is maximum when
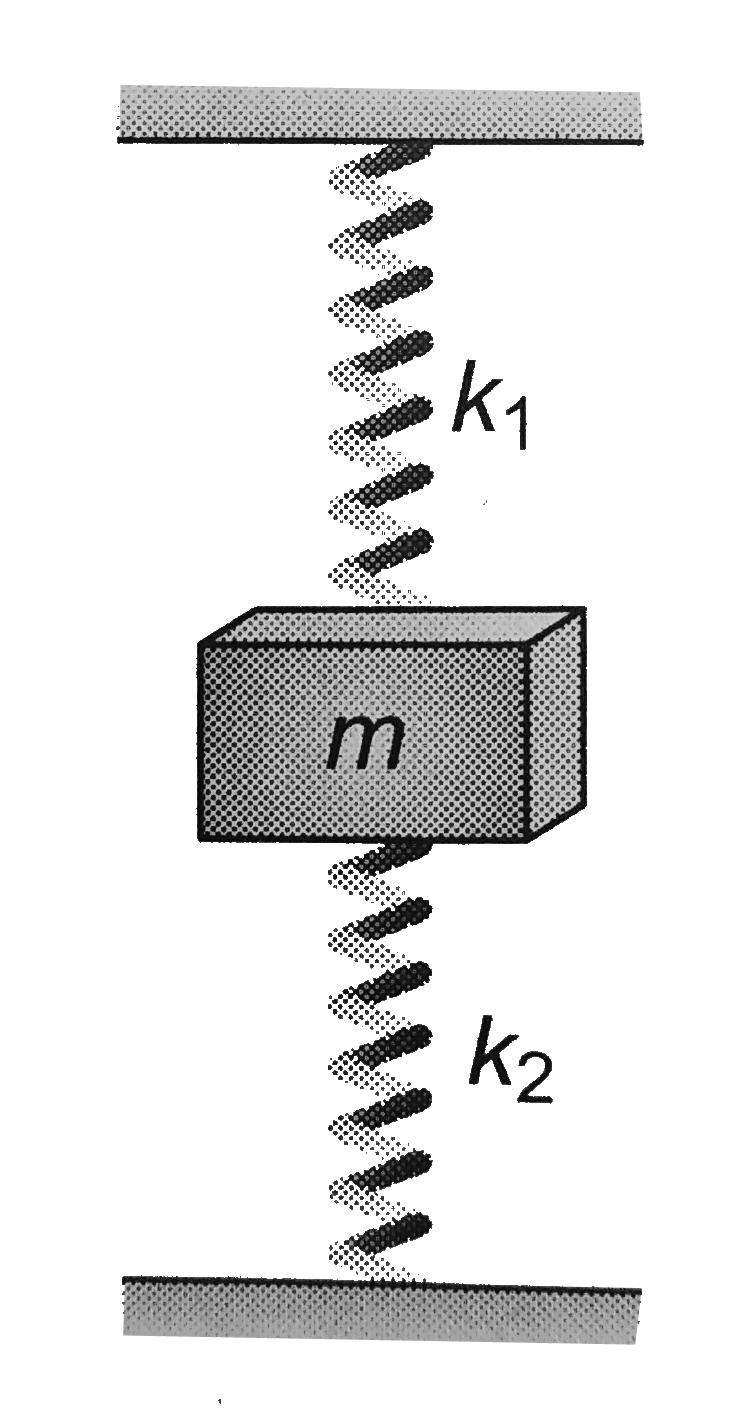
View SolutionIn the adjoining diagram the ball A is released from rest when the spring is at its natural length (neither stretched nor compressed) For the block B of mass M to leave contact with the ground at some time, the minimum mass of A must be:

View SolutionIn a gravity free space, man of mass M standing at a height h above the floor, throws a ball of mass m straight down with a speed u. When the ball reaches the floor, the distance of the man above the floor will be.
View Solution
