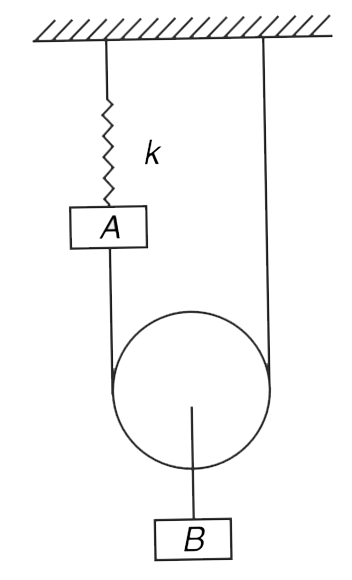
(i) In the system shown in figure, find the time period of vertical oscillations of the block A. Both the blocks A and B have equal mass of m and the force constant of the ideal spring is k. Pulley and threads are massless
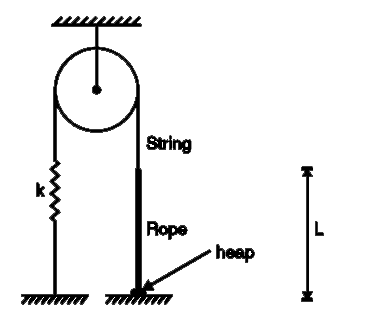
(ii) In the arrangement shown in the figure the spring, string and the pulley are mass less. The force constant of the spring is k. A rope of mass per unit length equal to λ(kgm−1) hangs from the string as shown. In equilibrium a length L of the rope is in air and its bottom part lies in a heap on the floor. The rope is very thin and size of the heap is negligible though the heap contains a fairly long length of the rope. The rope is raised by a very small distance and released. Show that motion will be simple harmonic and calculate the time period. Assume that the hanging part of the rope does not experience any force from the heap or the floor (For example there is no impact force while the rope hits the floor while moving downward and there is no impulsive pull when the vertical part jerks a small element of heap into motion).
The correct Answer is:(i) T=π√5mk,(ii)T=2π√λLk+lmadag
Step by step video, text & image solution for (i) In the system shown in figure, find the time period of vertical oscillations of the block A. Both the blocks A and B have equal mass of m and the force constant of the ideal spring is k. Pulley and threads are massless (ii) In the arrangement shown in the figure the spring, string and the pulley are mass less. The force constant of the spring is k. A rope of mass per unit length equal to lamda (kg m^(-1)) hangs from the string as shown. In equilibrium a length L of the rope is in air and its bottom part lies in a heap on the floor. The rope is very thin and size of the heap is negligible though the heap contains a fairly long length of the rope. The rope is raised by a very small distance and released. Show that motion will be simple harmonic and calculate the time period. Assume that the hanging part of the rope does not experience any force from the heap or the floor (For example there is no impact force while the rope hits the floor while moving downward and there is no impulsive pull when the vertical part jerks a small element of heap into motion). by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - ARIHANTCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 39videos
SIMPLE HARMONIC MOTION
- BOOK - ARIHANTCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 39videos
SIMPLE HARMONIC MOTION
- BOOK - ARIHANTCHAPTER - ROTATIONAL MOTIONEXERCISE - PHYSICS159videos
ROTATIONAL MOTION
- BOOK - ARIHANTCHAPTER - SURFACE TENSIONEXERCISE - Surface tension33videos
SURFACE TENSION
Similar Questions
The string, spring and the pulley shown in figure are light. Find the time period of the mass m.
 View Solution
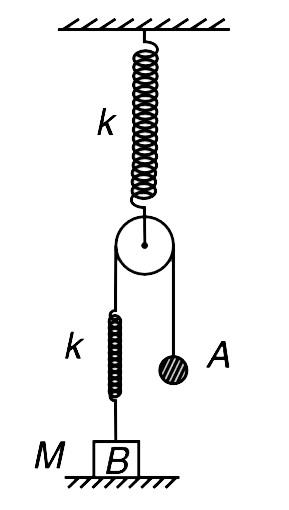
View SolutionIn the arrangement shown in the fig. string, springs and the pulley are mass less. Both the springs have a force constant of k and the mass of block B resting on the table is M. Ball A is released from rest when both the springs are in natural length and just taut. Find the minimum value of mass of A so that block B leaves contact with the table at some stage
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
In the situation as shown in figure time period of small vertical oscillation of block will be - (String, springs and pulley are ideal)
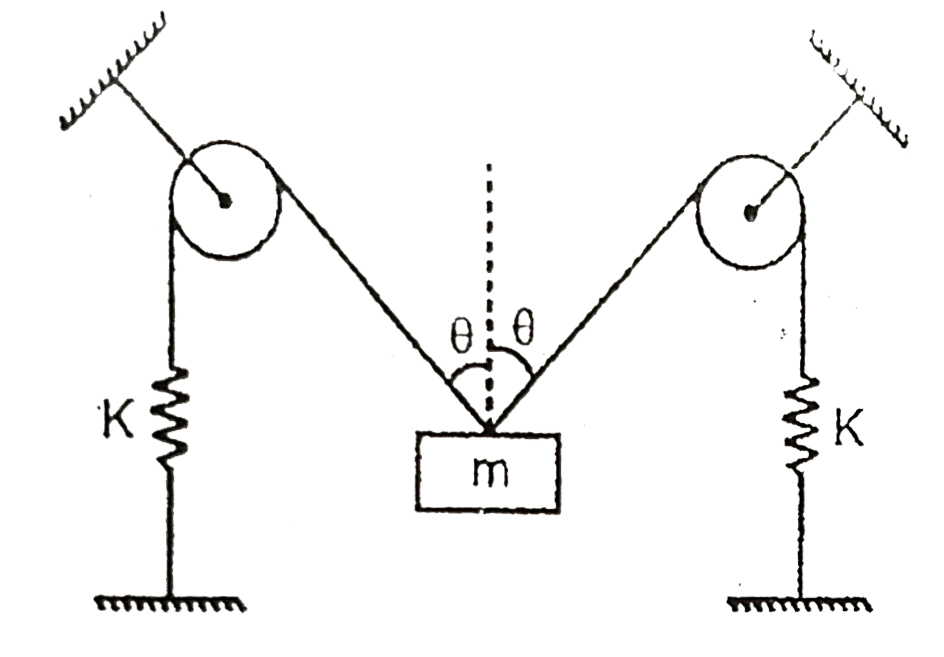 A2πcosθ√m2kB2πsecθ√m2kC2πsinθ√m2kD2πcosecθ√m2k
A2πcosθ√m2kB2πsecθ√m2kC2πsinθ√m2kD2πcosecθ√m2k - Question 2 - Select One
Find the time period of oscillation of block of mass m. Spring, and pulley are ideal. Spring constant is k.
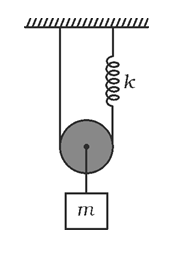 A2π√mkBπ√mkC4π√mkD2π√m2k
A2π√mkBπ√mkC4π√mkD2π√m2k - Question 3 - Select One
The period of the free oscillations of the system shown here if mass m1 is pulled down a little and force constant of the spring is k and masses of the fixed pulleys are negligible, is
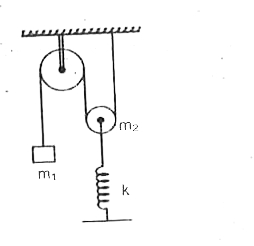 AT=2π√m1+m2kBT=2π√m1+4m2kCT=2π√4m1+m2kDT=2π√3m1+m2k
AT=2π√m1+m2kBT=2π√m1+4m2kCT=2π√4m1+m2kDT=2π√3m1+m2k
The string, the spring and the pulley shown in figure are light. Find the time period of the mass m.
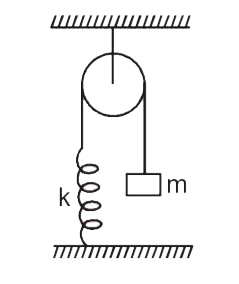 View Solution
View SolutionWhat would be the period of the free oscillations of the system shown here if mass M1 is pulled down a little force constant of the spring is k, mass of fixed pulley is negligible and movable pulley is smooth
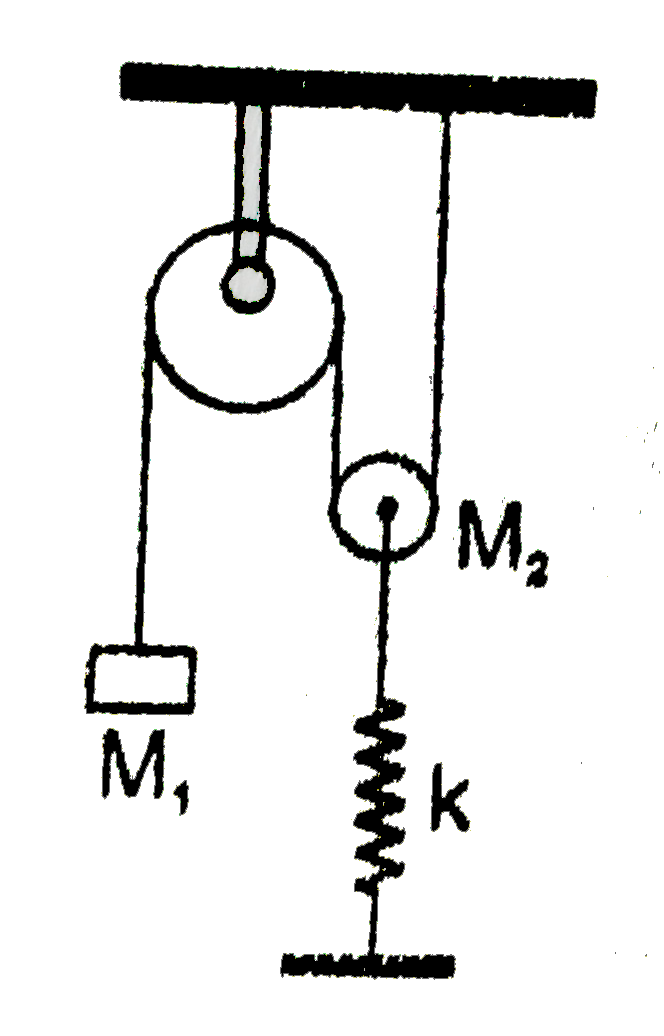 View Solution
View SolutionFind the acceleration of the block of mass m in the arrangement shown in the following figures. The masses of the pulleys and the threads, as well as the friction are assumed to be negligible.
 View Solution
View SolutionIn the arrangement shown in figure, pulleys are light and spring are ideal. K1, k2, k3and k4 are force constant of the spring. Calculate period of small vertical oscillations of block of mass m.
 View Solution
View SolutionBoth the blocks shown in figure have same mass 'm'. All the pulley and strings are massiess.
 View Solution
View Solution

