A block is being pulled slowly along a frictionless incline1 , [Fig. 3E. .3(a}.
( a) Show that the gravitationalforce is conservative . .
(b) Now.consider the incline tb be rough to show that frictional force is non-conservative...
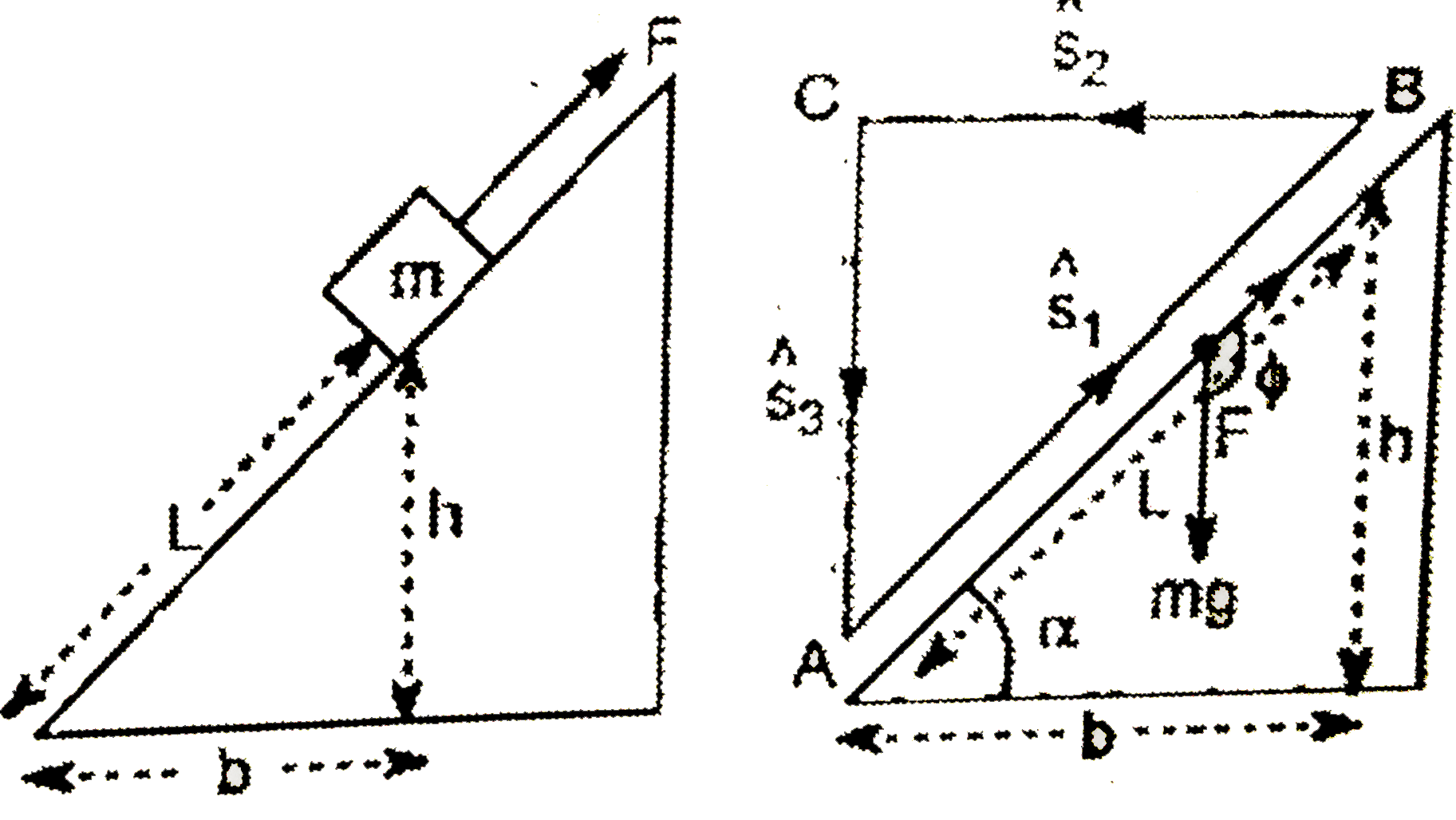
Step by step video & image solution for A block is being pulled slowly along a frictionless incline1 , [Fig. 3E. .3(a}. ( a) Show that the gravitationalforce is conservative . . (b) Now.consider the incline tb be rough to show that frictional force is non-conservative... by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- WORK AND ENERGYBOOK - ANURAG MISHRACHAPTER - WORK AND ENERGYEXERCISE - Level 1
53 Videos
- WORK AND ENERGYBOOK - ANURAG MISHRACHAPTER - WORK AND ENERGYEXERCISE - Level 2
18 Videos
- WORK AND ENERGYBOOK - ANURAG MISHRACHAPTER - WORK AND ENERGYEXERCISE - Matching types problems
14 Videos
- UNIT AND DIMENSIONSBOOK - ANURAG MISHRACHAPTER - UNIT AND DIMENSIONSEXERCISE - Matching Type Problem
4 Videos
Similar Questions

A block of mass 1 kg is pulled slowly along the curve path ACB by a tangential force as shown in figure. The magnitude of work done by the frictional force when the block moves from A to B is
View SolutionA block rests on a rough inclined plane as shown in Fig. 7.93 . A horizontal force is applied to it . (a) Find out the force of reaction .
(b) Can the force of friction be zero ? If yes , when ? (c) Assuming that , friction is not zero , find it magnitude and the direction of its limiting value .

View Solution
Knowledge Check
A block of mass m is being pulled up a rough incline by an agent delivering constant power P. The coefficient of friction between the block and the incline is μ. The maximum speed of the block during the course of ascent is
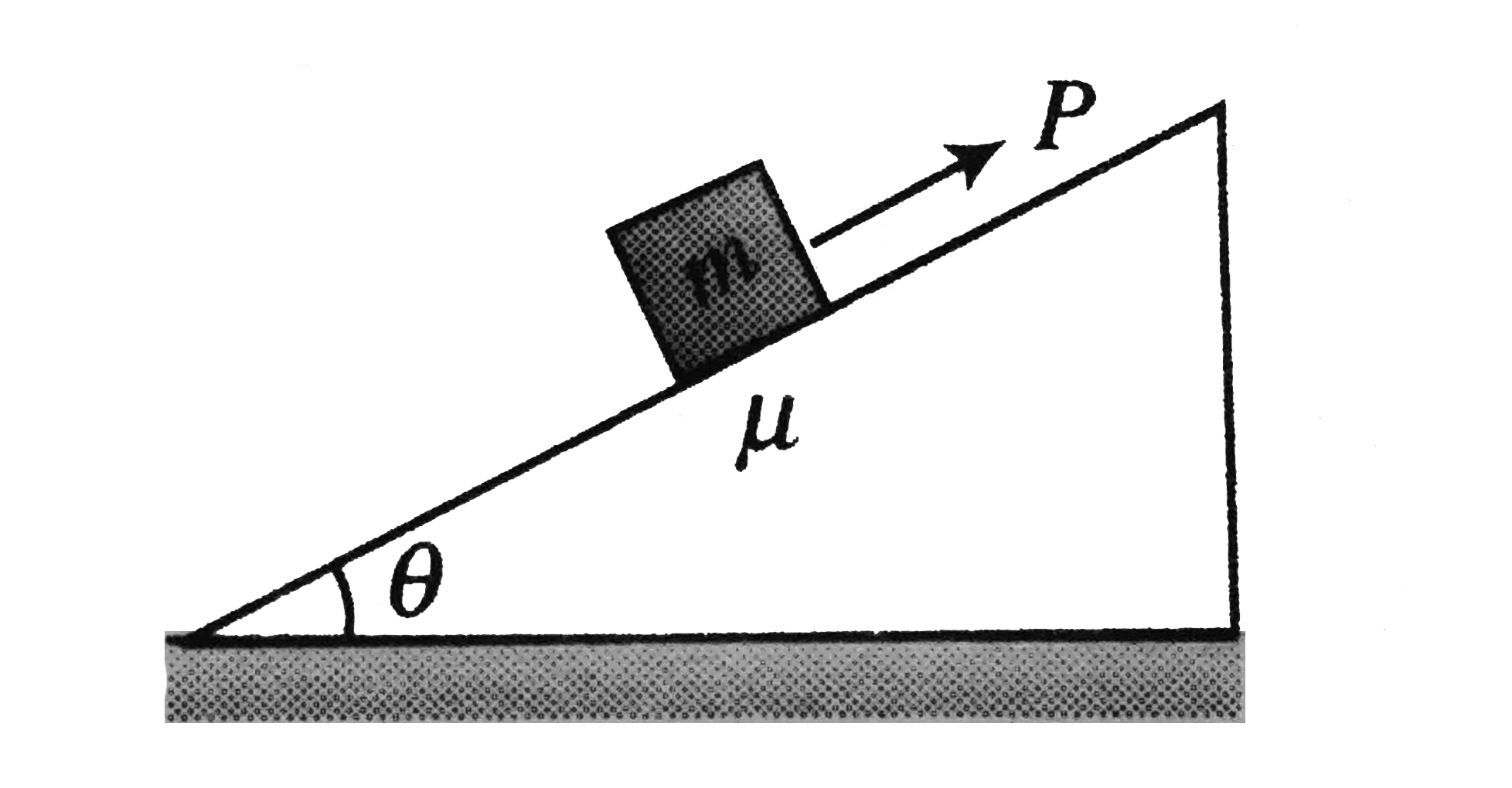 A(a) Pmgsinθ+μmgcosθB(b) Pmgsinθ−μmgcosθC(c) 2Pmgsinθ−μmgcosθD(d) 3Pmgsinθ−μmgcosθ
A(a) Pmgsinθ+μmgcosθB(b) Pmgsinθ−μmgcosθC(c) 2Pmgsinθ−μmgcosθD(d) 3Pmgsinθ−μmgcosθ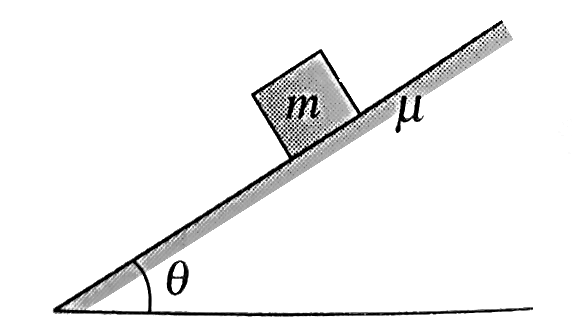 A block of mass m is placed on a rough inclined plane. The corfficient of friction between the block and the plane is μ and the inclination of the plane is θ.Initially θ=0 and the block will remain stationary on the plane. Now the inclination θ is gradually increased . The block presses theinclined plane with a force mgcosθ. So welding strength between the block and inclined is μmgcosθ, and the pulling forces is mgsinθ. As soon as the pulling force is greater than the welding strength, the welding breaks and the blocks starts sliding, the angle θ for which the block start sliding is called angle of repose (λ). During the contact, two contact forces are acting between the block and the inclined plane. The pressing reaction (Normal reaction) and the shear reaction (frictional force). The net contact force will be resultant of both.
A block of mass m is placed on a rough inclined plane. The corfficient of friction between the block and the plane is μ and the inclination of the plane is θ.Initially θ=0 and the block will remain stationary on the plane. Now the inclination θ is gradually increased . The block presses theinclined plane with a force mgcosθ. So welding strength between the block and inclined is μmgcosθ, and the pulling forces is mgsinθ. As soon as the pulling force is greater than the welding strength, the welding breaks and the blocks starts sliding, the angle θ for which the block start sliding is called angle of repose (λ). During the contact, two contact forces are acting between the block and the inclined plane. The pressing reaction (Normal reaction) and the shear reaction (frictional force). The net contact force will be resultant of both.
Answer the following questions based on above comprehension:
Q. If μ=34 then what will be frictional force (shear force) acting between the block and inclined plane when θ=30∘:A3√38mgBmg2C√32mgDzero A block of mass m is placed on a rough inclined plane. The corfficient of friction between the block and the plane is μ and the inclination of the plane is θ.Initially θ=0 and the block will remain stationary on the plane. Now the inclination θ is gradually increased . The block presses theinclined plane with a force mgcosθ. So welding strength between the block and inclined is μmgcosθ, and the pulling forces is mgsinθ. As soon as the pulling force is greater than the welding strength, the welding breaks and the blocks starts sliding, the angle θ for which the block start sliding is called angle of repose (λ). During the contact, two contact forces are acting between the block and the inclined plane. The pressing reaction (Normal reaction) and the shear reaction (frictional force). The net contact force will be resultant of both.
A block of mass m is placed on a rough inclined plane. The corfficient of friction between the block and the plane is μ and the inclination of the plane is θ.Initially θ=0 and the block will remain stationary on the plane. Now the inclination θ is gradually increased . The block presses theinclined plane with a force mgcosθ. So welding strength between the block and inclined is μmgcosθ, and the pulling forces is mgsinθ. As soon as the pulling force is greater than the welding strength, the welding breaks and the blocks starts sliding, the angle θ for which the block start sliding is called angle of repose (λ). During the contact, two contact forces are acting between the block and the inclined plane. The pressing reaction (Normal reaction) and the shear reaction (frictional force). The net contact force will be resultant of both.
Answer the following questions based on above comprehension:
Q. For what value of θ will the block slide on the inclined plane:Aθ>tan−1μBθ<tan−1μCθ>cot−1μDθ<cot−1μ
In fig Block m2 is loaded on block m1 . If there is no relative sliding between the block and the inclined plane is smooth , find the friction force between the block

View SolutionAn inclined plane of angule a is fixed onto a horizontal turntable with its line of greater slope in same plane as a diameter of forntable .A small block is placed on the inclined plane a distance r from the axis the coefficient of fraction between the block and the inclined plane is μ The turntable along with incline plane spins about its axis with constant minimum angular velocity ω
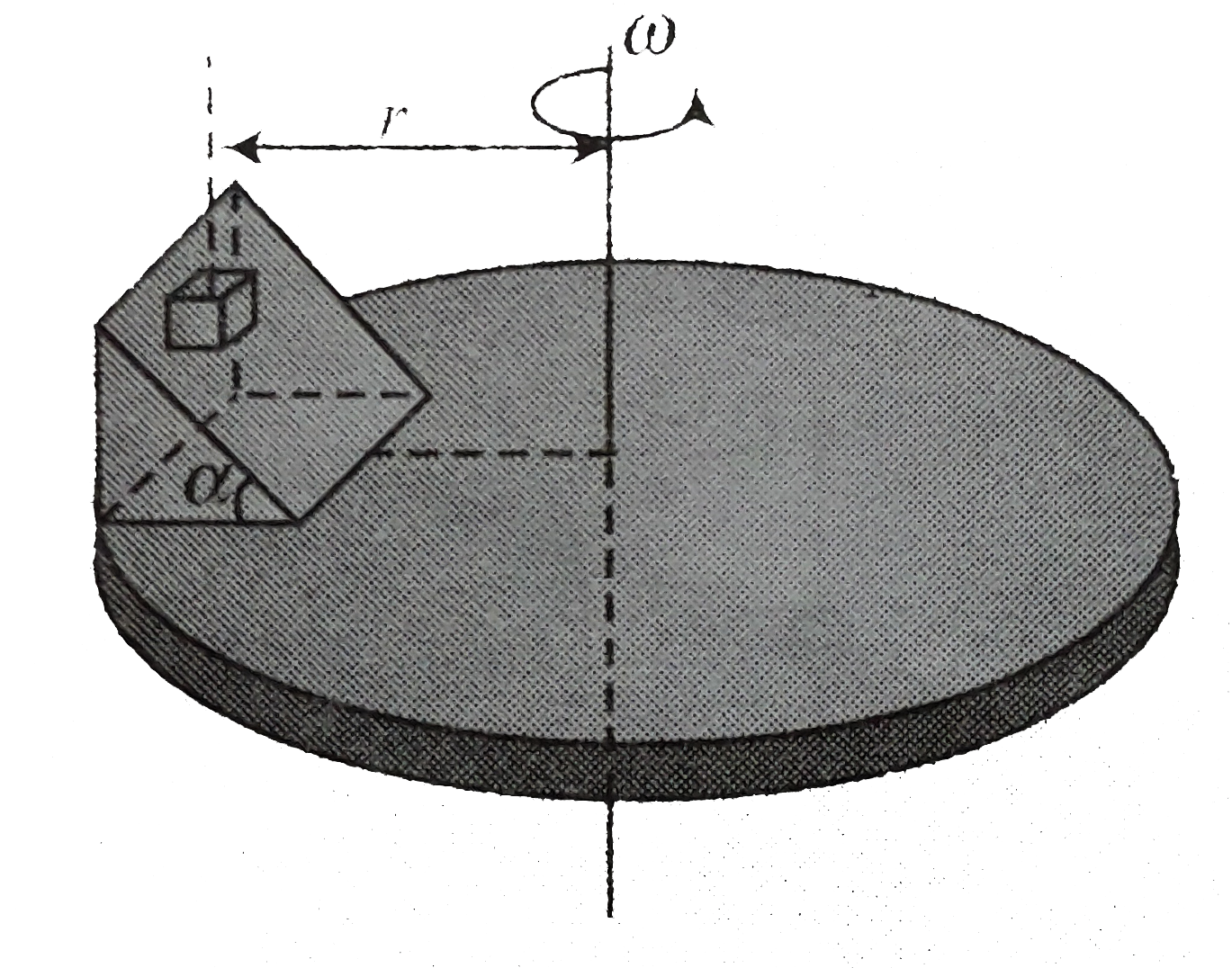
a. Find an capression for the minimum angular velocity ω to prevent the block from sliding down the plane in term of g,r,μ and the plane ω
b. Now a block of mass but having coefficient friction (with inclined plane)2μ is kept instead of the original block . find the radius of friction force acting between block and incline now to the friction force active in part (a)
View SolutionA long chain of mass of mass M length L is being pulled with constant velocity on a rough incline with coefficient of friction μ. What rate frictional force on chain is increasing

View Solution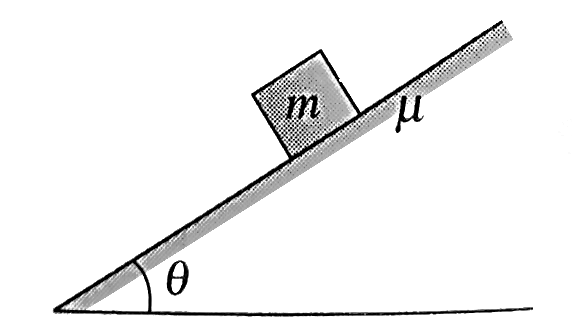 A block of mass m is placed on a rough inclined plane. The corfficient of friction between the block and the plane is μ and the inclination of the plane is θ.Initially θ=0 and the block will remain stationary on the plane. Now the inclination θ is gradually increased . The block presses theinclined plane with a force mgcosθ. So welding strength between the block and inclined is μmgcosθ, and the pulling forces is mgsinθ. As soon as the pulling force is greater than the welding strength, the welding breaks and the blocks starts sliding, the angle θ for which the block start sliding is called angle of repose (λ). During the contact, two contact forces are acting between the block and the inclined plane. The pressing reaction (Normal reaction) and the shear reaction (frictional force). The net contact force will be resultant of both.
A block of mass m is placed on a rough inclined plane. The corfficient of friction between the block and the plane is μ and the inclination of the plane is θ.Initially θ=0 and the block will remain stationary on the plane. Now the inclination θ is gradually increased . The block presses theinclined plane with a force mgcosθ. So welding strength between the block and inclined is μmgcosθ, and the pulling forces is mgsinθ. As soon as the pulling force is greater than the welding strength, the welding breaks and the blocks starts sliding, the angle θ for which the block start sliding is called angle of repose (λ). During the contact, two contact forces are acting between the block and the inclined plane. The pressing reaction (Normal reaction) and the shear reaction (frictional force). The net contact force will be resultant of both.
Answer the following questions based on above comprehension:
Q. If the entire system, were accelerated upward with acceleration a the angle of repose, would:
View SolutionA block of mass m is being pulled up the rough incline , inclined at angle θ with horizontal by an agent delivering constant power P. The coefficient of friction between block & incline is μ. Then during the upward motion along the inclined plane , maximum velocity of the block will be :
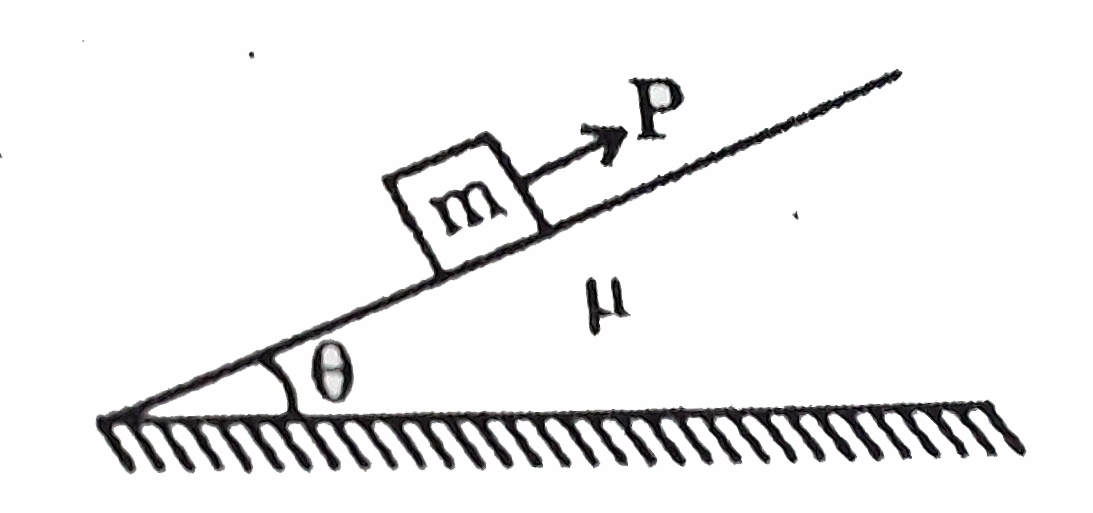
View Solution
