A block is mass m moves on as horizontal circle against the wall of a cylindrical room of radius R. The floor of the room on which the block moves is smooth but the friction coefficient between the wall and the block is μ. The block is given an initial speed v0. As a function of the speed v write a. the normal force by the wall on the block. b. the frictional force by the wall and c. the tangential acceleration of the block. d. Integrate the tangential acceleration (dvdt=vdvds) to obtain the speed of the block after one revoluton.Solution in Tamil
The correct Answer is:A, B, C, D
A block of mass m mioves on a horizontla circle against the wall of a cylindrical room of radius R.
Friction coefficient between wall annd the block is m.
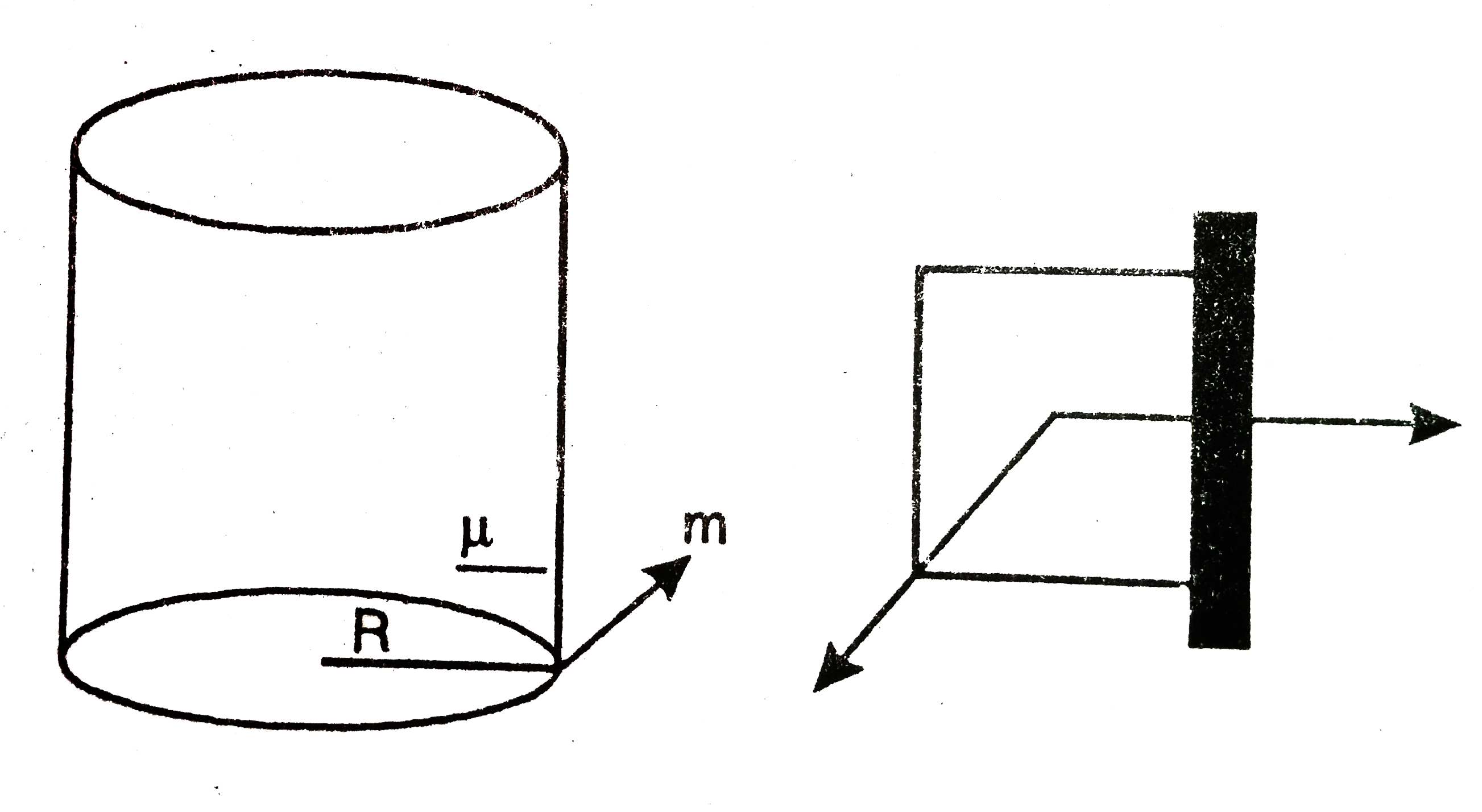 a. Normal reaction by the wall on the block is =mv2r
a. Normal reaction by the wall on the block is =mv2r
b. ∴FrictioNAlforcebywall<br>=(mumv^2)/r<br>c.(mumv^2)/R=ma<br>→a=−μv2R (Deceleration)
d. Now ((dv)/(dt)=v((dv)/(ds))=-(muv^2)/R<br>rarr ds=-r/mu (dv)/v<br>rarr s=-R/mu In v+c<br>Ats=0,v=v_0<br>Therefore,c=R/muIn v_0<br>So,s=-R/mu In v/v_0<br>rarr v/v_0=e^((mus)/R)<br>rarr For one rotation
s=2πR
So,v=v0e−2πμ
Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - HC VERMACHAPTER - CIRCULAR MOTIONEXERCISE - Objective -2
7 Videos
- CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONBOOK - HC VERMACHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Exercises
64 Videos
- FLUID MECHANICSBOOK - HC VERMACHAPTER - FLUID MECHANICSEXERCISE - All Questions
96 Videos
Similar Questions
An object follows a curved path. The following quantities may remain constant during the motion
View SolutionThree particles of masses 1.0 kg 2.0 kg and 3.0 kg are placed at the corners A,B and C respectively of an equilateral triangle ABC of edge 1m. Locate the centre of mass of the system.
View SolutionWater is filled in a flask up to a height of 20 cm. The bottom of the flask is circular with radius 10 cm. If the atmospheric pressure is 1.01×105 Pa, find the force exerted by the water on the bottom. Take g=10ms−2 and density of water =1000 kgm^-3.
View SolutionA block of mass 0.1 is held against a wall applying a horizontal force of 5N on block. If the coefficient of friction between the block and the wall is 0.5, the magnitude of the frictional force acting on the block is:
View SolutionA block mass m moves on a horizontal circle against the wall of a cylinderical room of radius R . The floor of the room, on which the block moves, is smooth but the friction coefficient between the wall and the block is mu . The block is given an initial speed V_(0) . the power developed by the resultant force acting on the block as a function of distance travelled s is
View Solutionएक बेलनाकार कमरे की दीवार से सटकर एक छोटा गुटका फर्श पर वृत्ताकार पथ में घूम रहा है। कमरे की त्रिज्या R तथा गुटके का द्रव्यमान m है। कमरे का फर्श घर्षणरहित माने तथा दीवार तथा गुटके के बीच घर्षण गुणांक μ ले। गुटके को प्रारंभिक चाल v0 देकर छोड़ दिया जाता है और वृत्ताकार पथ पर उसकी चाल घटती जाती है। गुटके की चाल के पदों में निकाले (a) दीवार द्वारा गुटके पर लगाया गया अभिलंब बल , (b) दीवार द्वारा गुटके पर लगाया गया घर्षण बल, (c) गुटके का स्पर्शरेखीय त्वरण तथा (d) समीकरण dvdt=vdvds को अनुकलित (integrate) कर एक चक्कर के बाद गुटके की चाल।
View Solutionकिसी दीवार के विरुद्ध एक गुटके को स्थिर बनाये रखने के लिए 10 न्यूटन के क्षैतिज बल की आवश्यकता होती है | यदि दीवार और गुटके के मध्य घर्षण गुणांक 0.2 हो , तो गुटके का भार होगा -
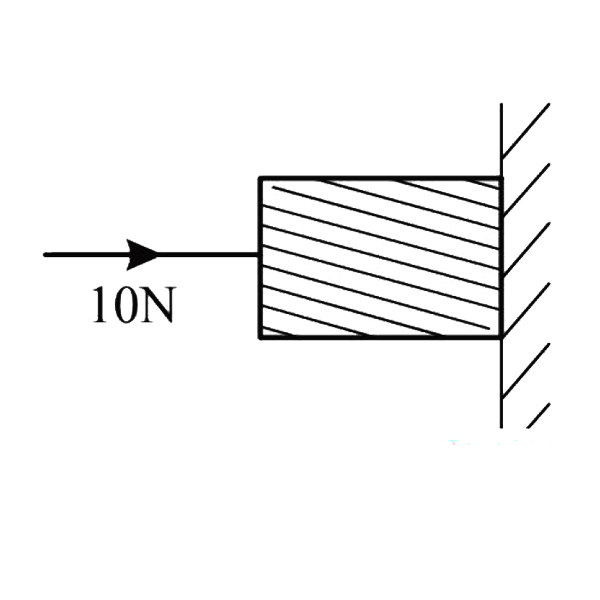
View SolutionA block of mass 1kg is pressed against a wall by applying a horizontal force of 10N on the block. If the coefficient of friction between the block and the wall is 0.5 ,magnitude of the frictional force acting on the block is
View Solutionकिसी M द्रव्यमान के एक गुटके को उंगलियों से दबाते हुए किसी ऊर्ध्वाधर दीवार से सटाकर रखा गया है। यदि गुटके व दीवार के मध्य घर्षण गुणांक μ है तथा गुरुत्वीय त्वरण g है, तो बताइए कि दीवार के विरुद्ध गुटके को उंगलियों से थामे रखने हेतु कितने न्यूनतम बल को आरोपित करने की आवश्यकता होती है?
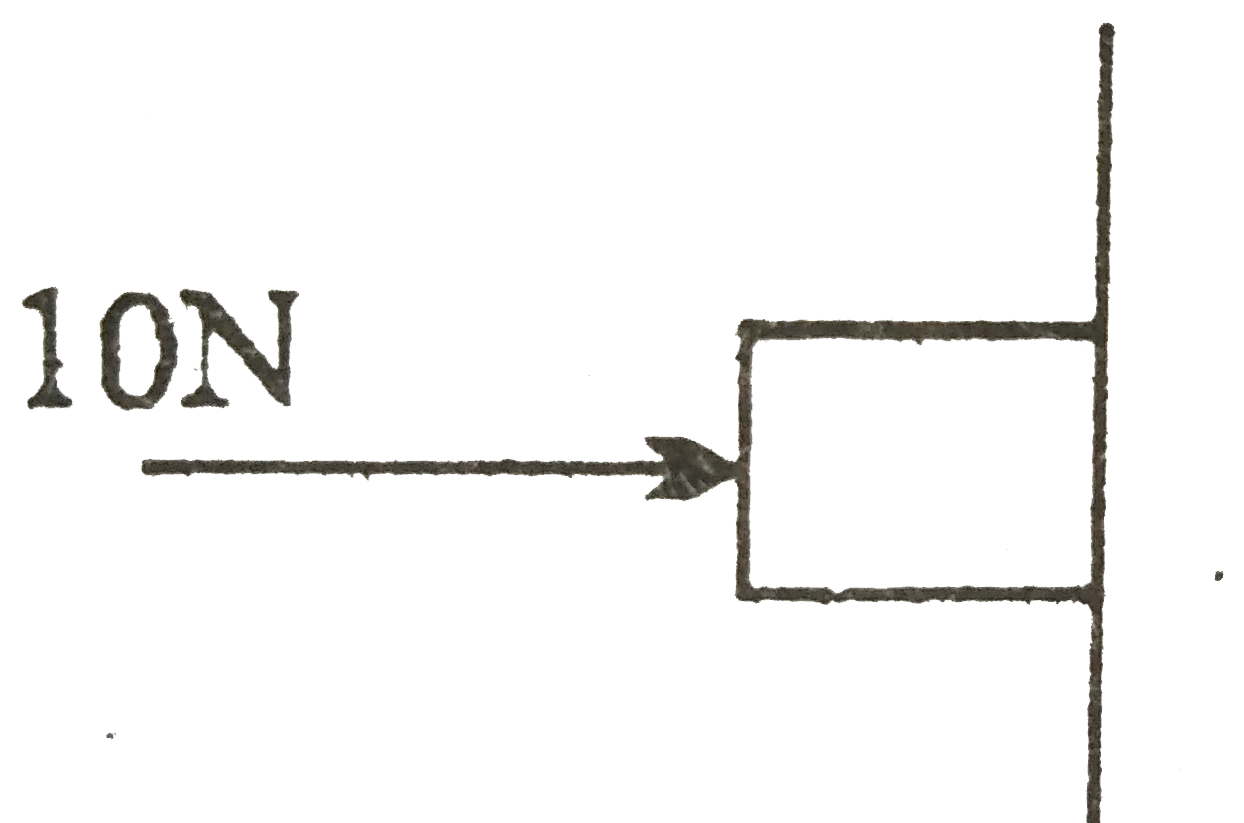
View SolutionA horizontal force of 10 N is necessary to just hold a block stationary against a wall. The coefficient of friction between the block and the wall is 0.2. The weight, of the block is:

View SolutionA block of mass 1 kg is pressed against a wall by applying a horizontal force of 10N on the block. If the coefficient of friction between the block and the wall is 0.5, magnitude of the frictional force acting on the block is
View SolutionA horizontal force of 10N is necessary to just hold a block stationary against as well. The coefficient of friction between the block and the wall is 0.2. The weight of the block is
View SolutionA horizontal force of 10 N is necessary to just hold a block stationary against a wall. The coefficient of friction between the block and the wall is 0.2. The weight of the block is
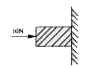
View SolutionA block of mass 1 kg is pressed against a wall by applying a horizontal force of 10 N on the block. If the coefficient of friction between the block and the wall is 0.5, magnitude of the frictional force acting on the block is
View SolutionA block of mass 0.1 kg is held against a wall by applying a horizontal force of 5N on the block. If the coefficient of friction between the block and the wall is 0.5, what is the magnitude of the frictional force acting on the block?
View SolutionA block of mass 0.1 kg is held against a wall applying a horizontal force of 5 N on the block. If the coefficient of friction between the block and the wall is 0.5, the magnitude of the frictional force acting on the block is :
View Solution
