A block mass m moves on a horizontal circle against the wall of a cylinderical room of radius R. The floor of the room, on which the block moves, is smooth but the friction coefficient between the wall and the block is μ. The block is given an initial speed V0. the power developed by the resultant force acting on the block as a function of distance travelled s is
μm30Re−3sμ
μmV30Re−3μsR
μmV30R
μmV30Re−3sR
The correct Answer is:B
f=−ma
⇒μN=−ma
=→μmV2R=−m×VdVdS
⇒μVR=−dVdS
⇒dVV=−μRdS
⇒∫VV0dVV=−μR∫S0dS
⇒ln∣∣∣VV0∣∣∣=−μR(S)
⇒V=V0e−μSR....(1)
Now power consumed by friction,
P=−f.V
=−μNV
=−μmV2RV
=−μmV3R......(2)
substituting the value of V from eq (1), we get
P=−μmRV30e−3μSR
Topper's Solved these Questions
- SYSTEM OF PARTICLESBOOK - NARAYNACHAPTER - SYSTEM OF PARTICLESEXERCISE - Level-V
72 Videos
- PHYSICAL WORLDBOOK - NARAYNACHAPTER - PHYSICAL WORLDEXERCISE - C.U.Q
10 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - EXERCISE - IV
39 Videos
Similar Questions
A block os mass m moves on as horizontal circle against the wall of a cylindrical room of radius R. The floor of the room onwhich the block moves is smoth but the friction coefficient between the wall and the block is μ. The block is given an initial speed v0. As a function of the speed v write a. the normal force by the wall on the block. b. thefrictional force by the wall and c. the tangential acceleration of the block. d. Integrate the tangential acceleration (dvdt=vdvds) to obtain the speed of the block after one revoluton.
View SolutionFind out the distance travelled by the block as shown in figure. If the initial speed of the block is v and μ is the friction coefficient between the surface of block and ground.
View Solution
Knowledge Check
A block of mass m is pulled by a force of constant power P placed on a rough horizontal plane. The friction coefficient between the block and the surface is μ. Then
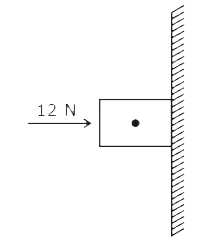
AThe maximum velocity of the block during the motion is PμmgBThe maximum velocity of the block during the motion is P2μmgCThe block's speed is never decreasing and finally becomes constantDThe speed of the block first increases to a maximum value and then decreasesA block of weight 5 N is pushed against a vertical wall by a force 12 N . The coefficient of friction between the wall and block is 0.6 . Find the magnitude of the force exerted by the wall on the block :
 A12 NB13 NC17 ND16 N
A12 NB13 NC17 ND16 NA block of mass 4 kg is kept on a rough horizontal surface. The coefficient of static friction is 0.8. If a force of 19 N is applied on the block parallel to the floor, then the force of friction between the block and floor is
A32 NB18 NC19 ND9.8 N
A 250 g block slides on aeroug horizontal table. Find the work donen by the frictinal force in bringing the block to rest if it is initially moving at a speed of 40 cm/s. If the friction coefficient between te table and the block is 0.1 how far does the block move before coming to rest?
View SolutionA block of mass 1kg is pressed against a wall by applying a horizontal force of 10N on the block. If the coefficient of friction between the block and the wall is 0.5 ,magnitude of the frictional force acting on the block is
View SolutionA block of mass m is kept on a horizontal table. If the static friction coefficient is μ., find the frictional force acting on the block.
View SolutionA block of weight 5N is pushed against a vertical wall by a force 12 N. The coefficient of friction between the wall and block is 0.6. The magnitude of the force exerted by the wall on the block is
View SolutionA force of 100N is applied on a block of mass 3kg as shown below. The coefficient of friction between wall and the block is 1/4. The friction force acting on the block is :
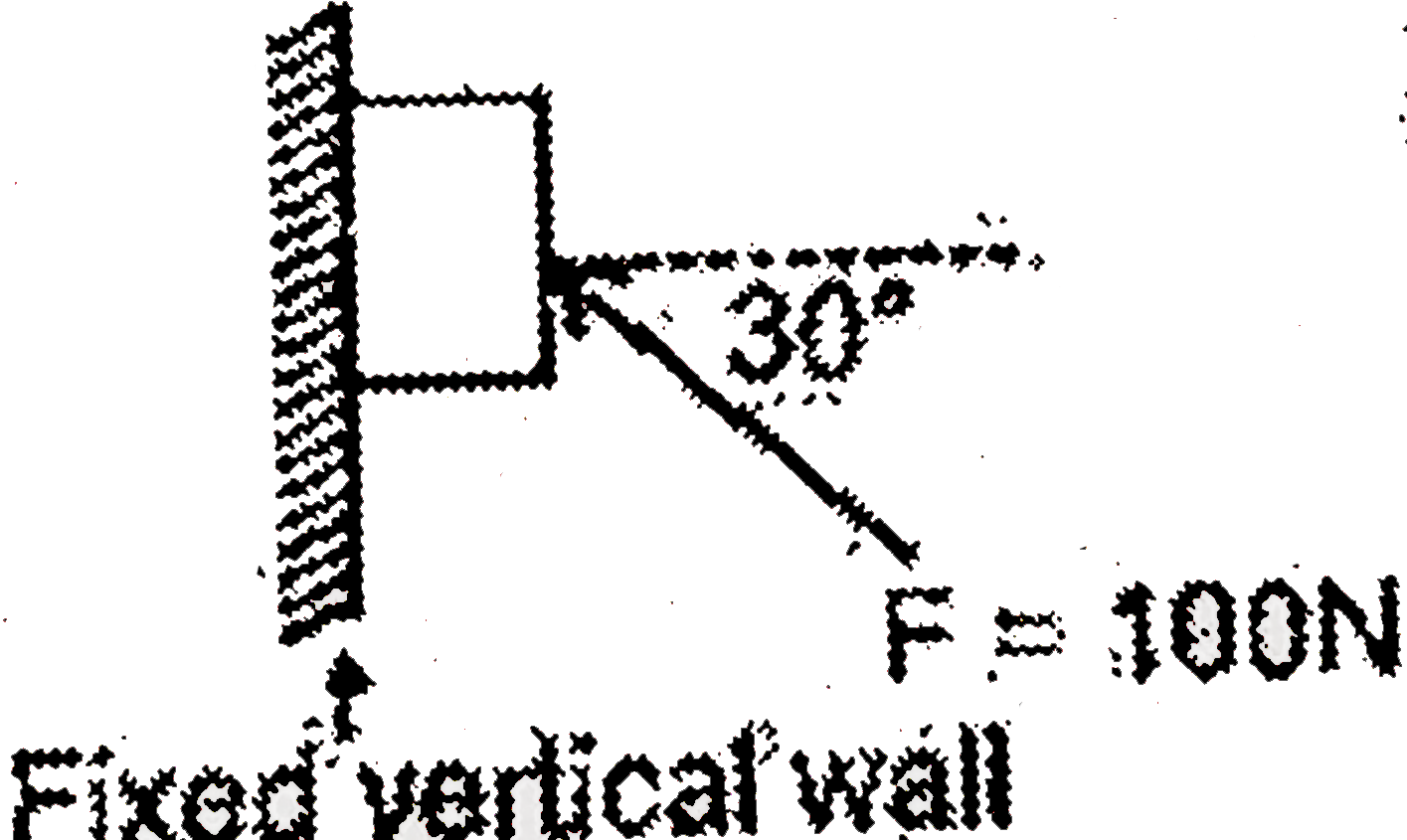
View Solution
