A block is placed on a horizontal surface. The block is pushed by applying a force F which acts at an angle of with the vertical . How much force will be required to move the block if friction coefficient ? Discuss the fact it .
Normal reaction force , N = (mg+Fcos)
Minimum required force (horizontal ) to move the block, )
Now,
If than
]
i.e.,
The block remains static.

Topper's Solved these Questions
- FRICTION BOOK - CHHAYA PUBLICATIONCHAPTER - FRICTION EXERCISE - EXAMINATION ARCHIVE with solutions (WBJEE )
3 Videos
- FRICTION BOOK - CHHAYA PUBLICATIONCHAPTER - FRICTION EXERCISE - EXAMINATION ARCHIVE with solutions ( JEE Main )
2 Videos
- FRICTION BOOK - CHHAYA PUBLICATIONCHAPTER - FRICTION EXERCISE - ENTRANCE CORNER ( Integer answer type )
1 Videos
- FIRST AND SECOND LAW OF THERMODYNAMICSBOOK - CHHAYA PUBLICATIONCHAPTER - FIRST AND SECOND LAW OF THERMODYNAMICSEXERCISE - CBSE SCANNER
18 Videos
- HYDROSTATICSBOOK - CHHAYA PUBLICATIONCHAPTER - HYDROSTATICSEXERCISE - CBSE SCANNER
1 Videos
Similar Questions
A block placed on a horizontal surface is being pushed by a force F making an angle θ with the vertical. If the friction coefficient is μ. How much force is needed to get the block just started. Discuss the situation when tanθ<μ.
View SolutionA block placed on a horizotnal surface is being pushed by a force F making an angle θ with the vertical. If the friction coefficient is μ. How much force is needed to get the block just started. Discuss the situation when tanθ<μ.
View Solution
Knowledge Check
A block of mass m is placed at rest on a horizontal rought surface with angle of friction ϕ. The block is pulley with a force F at an angle θ with the horizontal. The minimum value of F required to move the block is
Amgsinϕcos(θ−ϕ)Bmgcosϕcos(θ−ϕ)CmgtanϕDmgsinϕA block of mass m is lying on horizontal surface of coefficient of friction μ. A force is applied to the block at an angle θ with the horizontal. The block will move with a minimum force F if
Aμ=tanθBμ=cosθCμ=sinθDμ=cotθA block of mass m is pulled along a horizontal surface by applying a force at an angle θ with the horizontal. If the block travels with a uniform velocity and has a displacement d and the coefficient of friction is μ, then the work done by the applied force is
Aμmgdcosθ+μsinθBμmgdcosθcosθ+μcosθCμmgdsinθcosθ+μsinθDμmgdcosθcosθ−μsinθ
A block of mass m is placed at rest on a horizontal rough surface with angle of friction ϕ. The block is pulled with a force F at an angle θ with the horizontal. The minimum value of F required to move the block is
View SolutionA block of mass m is placed at rest on a horizontal rough surface with angle of friction ϕ. The block is pulled with a force F at an angle θ with the horizontal. The minimum value of F required to move the block is
View SolutionA block placed on a horizotnal surface is being pushed by a force F making an angle θ with the vertical. If the friction coefficient is μ. How much force is needed to get the block just started. Discuss the situation when tanθ<μ.
View SolutionA block placed on a horizontal surface is being pushed by a force F making an angle θ with the vertical as shown in Fig. 7.39 . The coefficient of friction between block and surface is μ . (a) Find the force required to slide the block with uniform velocity on the floor . (b) Show that if θ is smaller than a certain

angle θ0 , the block cannot be made to slide across the floor , no matter how great the force be .
View SolutionA block of mass m lying on a rough horizontal plance is acted upon by a horizontal force P and another force Q inclined at an angle θ to the vertical. The block will remain in equilibrium, if the coefficient of friction between it and the surface is
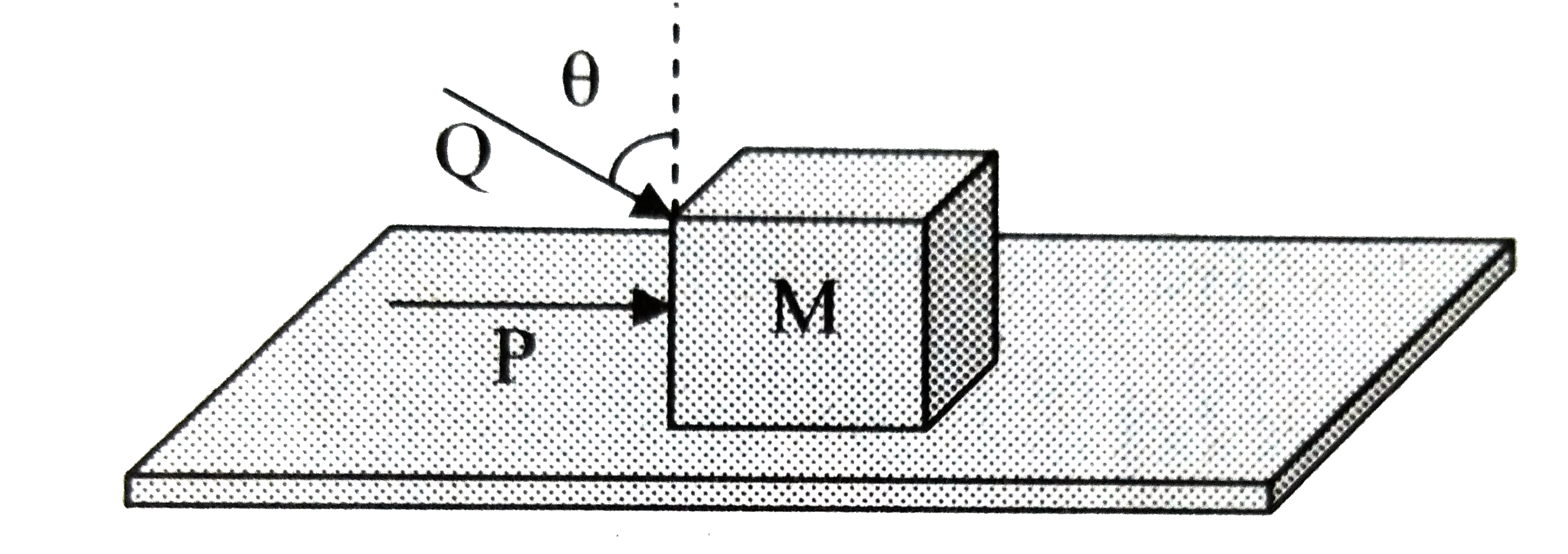
View Solution
