A block is placed on a rough horizontal plane. A time dependent horizontal force F=K t acts on the block K is a postive constant. Accelration-time graph of the block is
The correct Answer is:c
To solve the problem of finding the acceleration-time graph of a block subjected to a time-dependent horizontal force F=Kt on a rough horizontal plane, we can follow these steps:
Step 1: Understand the Forces Acting on the Block
The block is subjected to two forces:
1. The applied force F=Kt (which increases with time).
2. The frictional force f, which opposes the motion. The maximum static friction can be expressed as fmax=μmg, where μ is the coefficient of friction and m is the mass of the block.
Step 2: Determine the Condition for Motion
The block will not move until the applied force exceeds the maximum static friction. Therefore, we need to find the time t0 when the applied force equals the maximum static friction:
Kt0=μmg
From this, we can solve for t0:
t0=μmgK
Step 3: Analyze the Motion Before and After t0
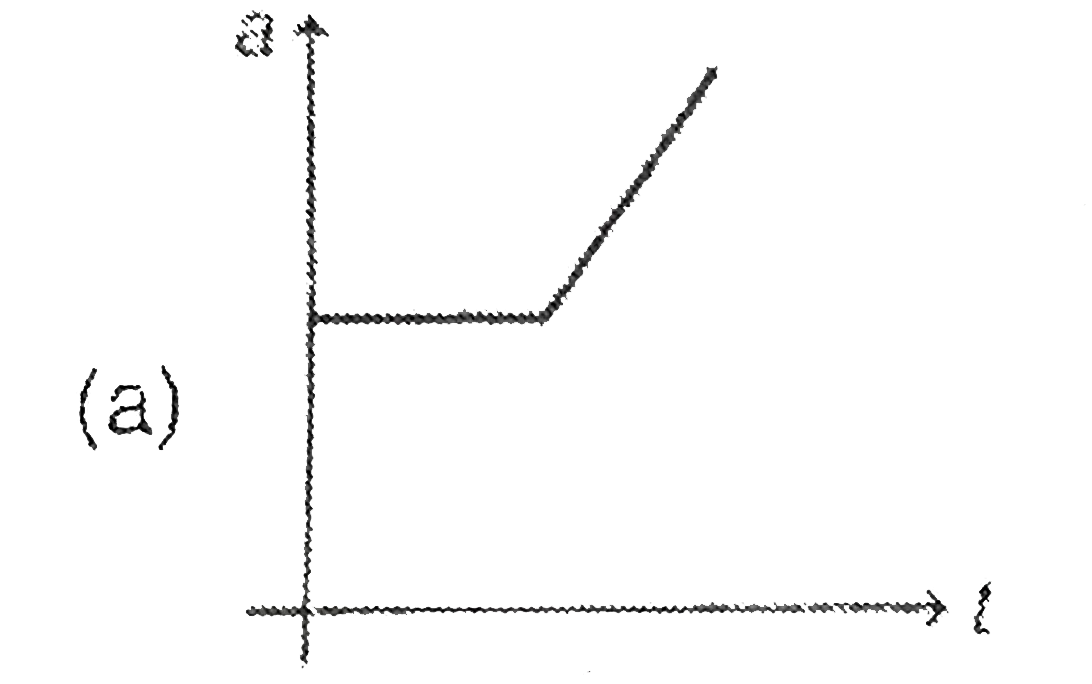
- For t<t0: The applied force F is less than the maximum static friction, so the block does not move. Thus, the acceleration a=0.
- For t≥t0: The applied force exceeds the maximum static friction, and the block starts to move. The net force acting on the block can be expressed as:
Fnet=Kt−fkinetic=Kt−μmg
Using Newton's second law, we can express the acceleration a as:
ma=Kt−μmg
Thus, the acceleration can be expressed as:
a=Kt−μmgm
This shows that the acceleration is directly proportional to time t for t≥t0.
Step 4: Sketch the Acceleration-Time Graph
- For t<t0: The acceleration is 0.
- For t≥t0: The acceleration increases linearly with time.
The graph will be a horizontal line at a=0 until t0, and then it will rise linearly with a slope of Km.
Final Result
The acceleration-time graph will have:
- A flat line at a=0 for t<t0.
- A straight line with a positive slope for t≥t0.
The block is subjected to two forces:
1. The applied force F=Kt (which increases with time).
2. The frictional force f, which opposes the motion. The maximum static friction can be expressed as fmax=μmg, where μ is the coefficient of friction and m is the mass of the block.
The block will not move until the applied force exceeds the maximum static friction. Therefore, we need to find the time t0 when the applied force equals the maximum static friction:
Kt0=μmg
From this, we can solve for t0:
t0=μmgK
- For t<t0: The applied force F is less than the maximum static friction, so the block does not move. Thus, the acceleration a=0.
- For t≥t0: The applied force exceeds the maximum static friction, and the block starts to move. The net force acting on the block can be expressed as:
Fnet=Kt−fkinetic=Kt−μmg
Using Newton's second law, we can express the acceleration a as:
ma=Kt−μmg
Thus, the acceleration can be expressed as:
a=Kt−μmgm
This shows that the acceleration is directly proportional to time t for t≥t0.
- For t<t0: The acceleration is 0.
- For t≥t0: The acceleration increases linearly with time.
The acceleration-time graph will have:
- A flat line at a=0 for t<t0.
- A straight line with a positive slope for t≥t0.
Similar Questions
A block of mass 4kg is placed on a rough horizontal plane A time dependent horizontal force F=kt acts on the block (k=2N/s). Find the frictional force between the block and the plane at t=2 seconds and t=5 seconds (μ=0.2) .
View SolutionA block of mass 5kg is placed on a rough horizontal plane.A time dependent horizontal force F=(t2+2t) N acts on the block. The friction force between the block and the plane at t=3s is (μ=0.4)
View Solution
Knowledge Check
A block is placed on a rough horizontal plane. A time-dependent horizontal force F=kt2 acts on the block. Here k is a positive constant. Acceleration -time graph of the block is
A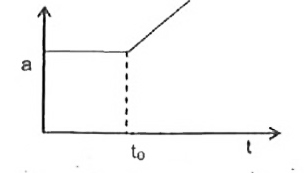 B
B C
C D
D
A block of mass 4kg is placed on a rough horizontal force plane. A time dependent horizontal force F=kt acts on the block. Here k=2Ns−1. The frictional force between the block and plane at time t=2s is (μ=0.2)
A4NB8NC12ND10NA block of mass 8 kg is placed on a rough horizontal plane. A time dependent force F=kt2acts on the block, where k=3N/s2. Coefficient of friction is0.6. Force of friction between the block and the plane at t=1s is
A48NB4NC2ND3N
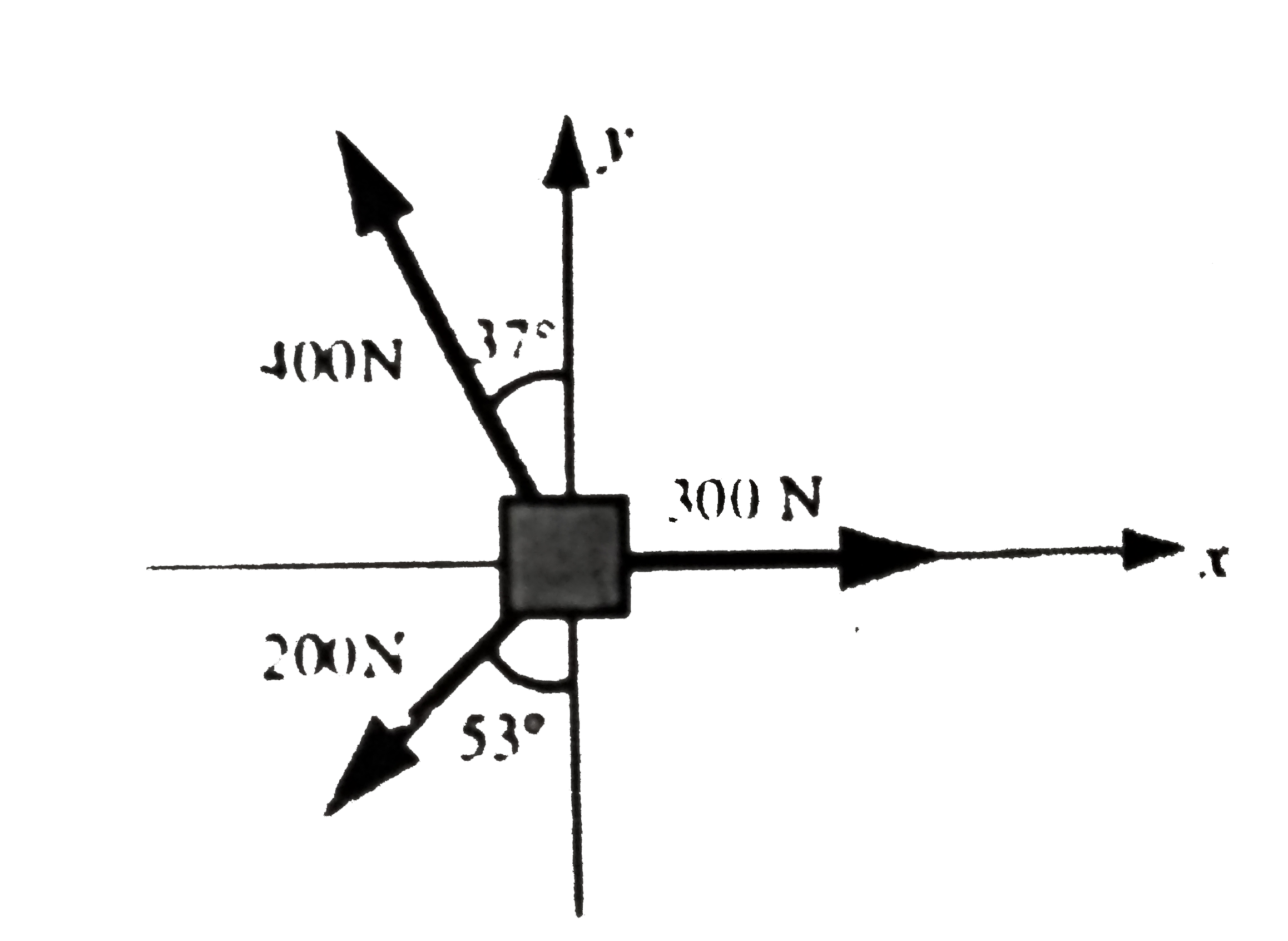
A block is placed on a rough horizontal plane. Three horizontalforces are applied on the block as shown in the figure. If the block is in equilibrium, find the friction force acting on the block.
View SolutionA block is placed on a smooth inclined plane as shown . For what value of horizontal force F, the block will remain at rest ?

View SolutionA block placed on a rough horizontal surface is pulled by a horizontal force F Let f be the force applied by the rough surface on the block . Plot a graph of f versus F .
View SolutionA block of mass 4kg is placed on a rough horizontal plane A time dependent force F=kt2 acts on the block where k=2N/s2 Coefficient of friction μ=0.8 force of friction between the block and the plane at t=2s is
View SolutionA block of unknown mass is at rest on a rough, horizontal surface. A horizontal force F is applied to the block. The graph in the figure shows the acceleration of the block with respect to the applied force. The mass of the block is

View Solution
