A block m1 of mass 10 kg kept on a rough, horizontal surface is connected to a sphere m2 of mass 1 kg by a string over an idcal pulley as shown in Fig. 6-18a. A force F of magnitude 50 N at an angle 37∘ with the horizontal is applied to the block as shown and the block slides to the right. The coefficient of kinetic friction between the block and surface is 0.1. Determine the magnitude of the acceleration of the two objects.

Figure 6-18 (a) A block of mass m, connected to sphere of mass m, by a string over an ideal pulley.
We cannot write the correct direction of kinetic friction till we know the correct direction of motion of the block. The way out is imagine if there was no friction then in which direction the bock would have moved. It is easy to calculate that in absence of friction the block would have moved toward right as the sphere will pull by its weight that is 10 N which is smaller than the horizontal component of force 40 N.
alculation: Now we can draw free-body diagrams for the two objects, as shown in Fig. 6-18b and Fig. 6-18c. The applied force has x and y components 40 N and 30 N, respectively. The magnitudes of the acceleration of the block and the acceleration of the sphere is →a.
Applying Newton.s second law to the block in the horizontal direction:
Fcosθ−fk−T=m1a

Applying Newton.s second law to the block in the vertical direction:
FN+Fsinθ−m1g=0
Applying Newton.s second law to the ball in the vertical direction:
T−m2g=m2a
Solve Eq. 6-25 for FN:
FN=m1g−Fsinθ
Substituting FN into fk=μkFN,
fk=μk(m1g−Fsinθ)=0.1(100−30)=7N
Substituting Eq. 6-27 and the value of T from Eq. 6-26 into Eq. 6-24,
40−7−1(a+g)=10a
and solving for →a:
→a=23/11m/s2
Note: If friction force would have been larger, the block would have been at rest.
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - FORCE AND MOTION-IIEXERCISE - CHECKPOINTS5videos
FORCE AND MOTION-II
- BOOK - RESNICK AND HALLIDAYCHAPTER - FORCE AND MOTION-IIEXERCISE - PROBLEMS33videos
FORCE AND MOTION-II
- BOOK - RESNICK AND HALLIDAYCHAPTER - FORCE AND MOTION - I EXERCISE - PRACTICE QUESTIONS (Integer Type)3videos
FORCE AND MOTION - I
- BOOK - RESNICK AND HALLIDAYCHAPTER - GAUSS' LAW EXERCISE - PRACTICE QUESTIONS (INTEGER TYPE)3videos
GAUSS' LAW
Similar Questions
A block of mass m is moving on a rough horizontal surface. μ is the coefficient of kinetic friction between the block and the surface. What is the net force exerted by the surface on the block?
View SolutionA wooden block of mass M resting on a rough horizontal surface is pulled with a force T at an angle q to the horizontal. If m is coefficient of kinetic friction between the block and the surface, the acceleration of the block is
View Solution
Knowledge Check
- Question 1 - Select One
A wooden block of mass M resting on a rough horizontal surface is pulled with a force F at an angle with the horizontal. If is the coefficient of kinetic friction between the block and the surface, then acceleration of the block is -
AFM(cosϕ+μsinϕ)−μgBFsin(ϕ)MCμFcosϕD,uFsinϕ - Question 2 - Select One or More
A block is kept on a rough horizontal surface as shown. Its mass is 2 kg and coefficient of friction between block and surface (μ)=0.5. A horizontal force F is acting on the block. When
 AF = 4 N, acceleration is zero.BF = 4 N, friction is 10 N and acceleration is 3m/s2.CF = 14 N, acceleration is 2m/s2.DF = 14 N, friction is 14 N.
AF = 4 N, acceleration is zero.BF = 4 N, friction is 10 N and acceleration is 3m/s2.CF = 14 N, acceleration is 2m/s2.DF = 14 N, friction is 14 N.
A block of mass m = 2kg is accelerating by a force F = 20N applied on a smooth light pulley as shown in the figure. If the coefficient of kinetic friction between the block and the surface is μ=0.3, find its acceleration.
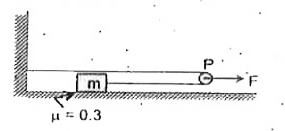 View Solution
View SolutionTwo blocks of masses 4kg and 6kg are kept on a rough horizontal surface as shown. If the acceleration of 6kg block is 5n, then n is :
 View Solution
View SolutionTwo blocks of masses 4kg and 6kg are kept on a rough horizontal surface as shown. If the acceleration of 6kg block is 5n, then n is :
 View Solution
View SolutionA block is kept on a rough horizontal surface as shown. Its mass is 2 kg and coefficient of friction between block and surface (μ)=0.5. A horizontal force F is acting on the block. When
 View Solution
View SolutionA block of mass 1 kg in kept on a rough horizontal surface with μs=0.1 . A force of 0.5 N is applied as shown in the figure. What is the frictional force applied by ground on the block?
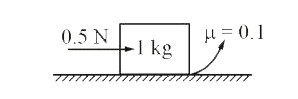 View Solution
View SolutionA block of mass 1 kg in kept on a rough horizontal surface with μs=0.1 . A force of 0.5 N is applied as shown in the figure. What is the frictional force applied by ground on the block?
 View Solution
View Solution

