A block of mass m is moving on a rough horizontal surface. μ is the coefficient of kinetic friction between the block and the surface. What is the net force exerted by the surface on the block?
mg√1+μ2
μmg
mg
mg√1−μ2
The correct Answer is:A
To find the net force exerted by the surface on a block of mass m moving on a rough horizontal surface with a coefficient of kinetic friction μ, we can follow these steps:
1. Identify the Forces Acting on the Block:
- The block experiences several forces:
- The gravitational force acting downwards: Fg=mg
- The normal force acting upwards from the surface: N
- The applied force F (if any) acting horizontally.
- The frictional force fk acting opposite to the direction of motion due to kinetic friction.
2. Determine the Normal Force:
- Since the block is on a horizontal surface and there is no vertical acceleration, the normal force N is equal to the gravitational force:
N=mg
3. Calculate the Frictional Force:
- The frictional force fk can be calculated using the coefficient of kinetic friction:
fk=μN=μmg
4. Net Force Calculation:
- The net force exerted by the surface on the block includes both the normal force and the frictional force. Since these forces act in perpendicular directions, we can find the resultant force using the Pythagorean theorem:
Fnet=√N2+f2k
- Substituting the values of N and fk:
Fnet=√(mg)2+(μmg)2
- Factoring out mg:
Fnet=mg√1+μ2
5. Final Result:
- Therefore, the net force exerted by the surface on the block is:
Fnet=mg√1+μ2
- The block experiences several forces:
- The gravitational force acting downwards: Fg=mg
- The normal force acting upwards from the surface: N
- The applied force F (if any) acting horizontally.
- The frictional force fk acting opposite to the direction of motion due to kinetic friction.
- Since the block is on a horizontal surface and there is no vertical acceleration, the normal force N is equal to the gravitational force:
N=mg
- The frictional force fk can be calculated using the coefficient of kinetic friction:
fk=μN=μmg
- The net force exerted by the surface on the block includes both the normal force and the frictional force. Since these forces act in perpendicular directions, we can find the resultant force using the Pythagorean theorem:
Fnet=√N2+f2k
- Substituting the values of N and fk:
Fnet=√(mg)2+(μmg)2
- Factoring out mg:
Fnet=mg√1+μ2
- Therefore, the net force exerted by the surface on the block is:
Fnet=mg√1+μ2
Similar Questions
A block of mass M is kept on as rough horizontal surface. The coefficient of static frictionbetween the block and the surface is μ. The block is to be pulled by applying a force to it. What minimum force is needed to slide the block? In which direction should this force act?
View SolutionA block of mass M is kept on as rough horizontal surface. The coefficient of static friction between the block and the surface is μ. The block is to be pulled by applying a force to it. What minimum force is needed to slide the block? In which direction should this force act?
View Solution
Knowledge Check
A block of mass 1 kg lies on a horizontal surface in a truck. The coefficient of static friction between the block and the surface is 0.6. If the acceleration of the truck is 5m/s2, the frictional force acting on the block is…………newtons.
A10NB5NC2.5ND20N
A block of mass M rests on a rough horizontal surface as shown. Coefficient of friction between the block and the surface is μ. A force F=mg acting at angle θ with the vertical side of the block pulls it. In which of the following cases the block can be pulled along the surface?

View SolutionAsseration : A block of mass m starts moving on a rough horizontal surface with a velocity v. It stops due to friction between the block and the surface after moving through a ceratin distance. The surface is now tilted to an angle of 30∘ with the horizontal and same block is made to go up on the surface with the same initial velocity v. The decrease in the mechanical energy in the second situation is small than the first situation.
Reason : The coefficient of friction between the block and the surface decreases with the increase in the angle of inclination.
View SolutionA block of mass 4 kg is kept over a rough horizontal surface. The coefficient of friction between the block and the surface is 0.1 At, t=0, (3ˆi)(ms) velocity is imported to the block simultaneously (−2ˆi)N force starts acting on it. Its displacement in first 5s is
View SolutionA block of mass 1 kg lies on a horizontal surface in a truck. The coefficient of static friction between the block and the surface is 0.6. If the acceleration of the truck is 5m/s2, the frictional force acting on the block is…………newtons.
View SolutionWhat is the value of applied force ‘F’ which is exerted at an angle θ with the horizontal on a block of mass ‘m’ placed on a horizontal rough surface, if the coefficient of static friction between the block and the surface is , such that the block is on the verge of moving horizontally?
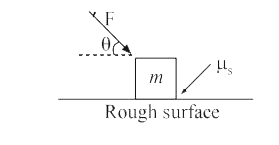
View Solution
A force F=2t is spplied at t=0 sec to the block of mass m placed on a rough horizontal surface. The coefficient of static and kinetic friction between the block and surface are μS and μk respectively. Which of the following graphs best represents the acceleration vs time of the block(μS>μk)?
View Solution
A force F=2t is spplied at t=0 sec to the block of mass m placed on a rough horizontal surface. The coefficient of static and kinetic friction between the block and surface are μS and μk rspectively. Which of the following graphs best represents the acceleration vs time of the block(μS>μk)?
View Solution
