A block of mass 1 kg is resting on a rough inclined plane which rises·3 in every 5. What is the minimum force required to move the block up the inclined plane ifµ == 0.5? (g=10m/s2)
10 N
8 N
6 N
4 N
The correct Answer is:A
To solve the problem of finding the minimum force required to move a block of mass 1 kg up a rough inclined plane, we can follow these steps:
Step 1: Determine the dimensions of the incline
The incline rises 3 units for every 5 units of horizontal distance. We can visualize this as a right triangle where:
- The height (opposite side) = 3
- The base (adjacent side) = 5
Using the Pythagorean theorem, we can find the length of the incline (hypotenuse):
Length of incline=√(32+52)=√(9+25)=√34
Step 2: Calculate the angle of inclination (θ)
We can find the angle θ using the sine function:
sinθ=oppositehypotenuse=3√34
And using the cosine function:
cosθ=adjacenthypotenuse=5√34
Step 3: Calculate the weight of the block
The weight (W) of the block is given by:
W=mg
Where:
- m=1kg
- g=10m/s2
Thus,
W=1×10=10N
Step 4: Resolve the weight into components
The weight of the block can be resolved into two components:
1. Parallel to the incline:
W∥=Wsinθ=10⋅3√34
2. Perpendicular to the incline:
W_{\perpendicular} = W \cos \theta = 10 \cdot \frac{5}{\sqrt{34}}
Step 5: Calculate the normal force (N)
The normal force (N) acting on the block is equal to the perpendicular component of the weight:
N = W_{\perpendicular} = 10 \cdot \frac{5}{\sqrt{34}}
Step 6: Calculate the frictional force (f)
The frictional force (f) opposing the motion is given by:
f=μN
Where μ=0.5:
f=0.5⋅(10⋅5√34)=25√34
Step 7: Calculate the minimum force (F)
The minimum force required to move the block up the incline must overcome both the gravitational component down the incline and the frictional force:
F=W∥+f=10⋅3√34+25√34
Combining the terms:
F=30+25√34=55√34
Step 8: Calculate the numerical value of F
To find the numerical value of F:
F≈555.831≈9.43N
Conclusion
The minimum force required to move the block up the inclined plane is approximately 9.43 N.
---
The incline rises 3 units for every 5 units of horizontal distance. We can visualize this as a right triangle where:
- The height (opposite side) = 3
- The base (adjacent side) = 5
Length of incline=√(32+52)=√(9+25)=√34
We can find the angle θ using the sine function:
sinθ=oppositehypotenuse=3√34
And using the cosine function:
cosθ=adjacenthypotenuse=5√34
The weight (W) of the block is given by:
W=mg
Where:
- m=1kg
- g=10m/s2
W=1×10=10N
The weight of the block can be resolved into two components:
1. Parallel to the incline:
W∥=Wsinθ=10⋅3√34
2. Perpendicular to the incline:
W_{\perpendicular} = W \cos \theta = 10 \cdot \frac{5}{\sqrt{34}}
The normal force (N) acting on the block is equal to the perpendicular component of the weight:
N = W_{\perpendicular} = 10 \cdot \frac{5}{\sqrt{34}}
The frictional force (f) opposing the motion is given by:
f=μN
Where μ=0.5:
f=0.5⋅(10⋅5√34)=25√34
The minimum force required to move the block up the incline must overcome both the gravitational component down the incline and the frictional force:
F=W∥+f=10⋅3√34+25√34
Combining the terms:
F=30+25√34=55√34
To find the numerical value of F:
F≈555.831≈9.43N
The minimum force required to move the block up the inclined plane is approximately 9.43 N.
Topper's Solved these Questions
- FRICTIONAL IN SOLIDS AND LIQUIDS BOOK - MARVEL PUBLICATIONCHAPTER - FRICTIONAL IN SOLIDS AND LIQUIDS EXERCISE - TEST YOUR GRASP
10 Videos
- FORCE, WORK AND TORQUEBOOK - MARVEL PUBLICATIONCHAPTER - FORCE, WORK AND TORQUEEXERCISE - TEST YOUR GRASP
10 Videos
- MAGNETIC EFFECT OF ELECTRIC CURRENT BOOK - MARVEL PUBLICATIONCHAPTER - MAGNETIC EFFECT OF ELECTRIC CURRENT EXERCISE - TEST YOUR GRASP
10 Videos
Similar Questions
A block of mass 10 kg rests on a rough inclined plane of inclination 45∘ with the horizontal. What minimum force is required to just move the block up the inclined plane. Given μs=0.5andg=10ms−2.
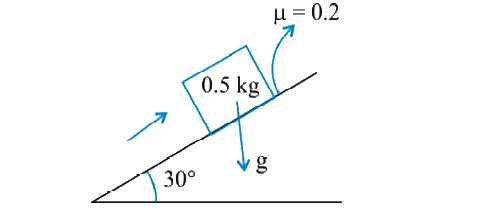
View SolutionA block of mass 0.5 kg is kept on a rough inclined plane making an angle of 30∘ with horizontal. What power will be required to move the block up the plane (along the plane) with a velocity of 5m/s ? (Take m = 0.2 between block and plane)
View Solution
Knowledge Check
A body of mass 10kg is lying on a rough inclined plane of inclination 37∘ and μ=1/2 , the minimum force required to pull the body up the plane is
A80NB100NC120ND60NA block weighing 10 kg just starts sliding down a rough inclined plane, which rises 5 in every 13 . What is the coefficient of friction ?
A0.325B0.515C0.416D0.632A block weighing 10 kg just starts sliding down a rough inclined plane, which rises 5 in every 13 . What is the coefficient of friction ?
A0.325B0.515C0.416D0.632
A block of mass 5 kg is at rest on a rough inclined surface. If angle of inclination of plane is 60∘, then force applied by it on block is
View SolutionA block of mass m is lying on an inclined plane. The coefficient of friction between the plane and the block is μ. The force (F1) required to move the block up the inclined plane will be:-
View SolutionA block of mass m is at rest on a rough inclined plane, whose friction coefficient is μ. Net force exerted by surface on block is :-
View SolutionA block of mass 3kg is at rest on a rough inclined plane as shown in the figure. The magnitude of net force exerted by the surface on the block will be

View SolutionA mass of 1 kg is just able to slide down the slope of a rough inclined surface when the angle of inclination is 60°. What is the minimum force necessary to pull the mass up the inclined plane?
(g=10m/s2)
View Solution
