A block of mass 1kg is tied to a string of length 1m the other end of which is fixed The block is moved on a smooth horizontal table with constant speed 10ms−1. Find the tension in the string
Choose a small element of width dx at a distance a from one end of the rod . The mass of the element dm=mldx Let T is the tension to the rod at a distance x by Newton's second law , from the motion of element of mass dm , we have
T−(T+dT)=dmω2xor−dT=(mldx)ω2x
Interating above equation we get
−∫0TdT=mω2l∫1x×dx
or−|T|0T=mω22l∣∣x2∣∣0x
or−(0−T)=mω22l(t2−x2)
orT=mω22l(t2−x2)
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Solved Examples12videos
NEWTON'S LAWS OF MOTION 2
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Exercise 7.125videos
NEWTON'S LAWS OF MOTION 2
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Integer5videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE2videos
PROPERTIES OF SOLIDS AND FLUIDS
Similar Questions
Two blocks o equal mass m are tied to each other through light string. One of the blocks is pulled along the line joining them with a constnt force F. Find the tension in the string joining the blocks.
View SolutionA block is tied to one end of a light string of length 1 whose other end is fixed to a rigid support. The block is given a speed of √7gl/2 from the lowermost position. Find the height and speed at which the block leaves the circle. Also find the maximum height to which it rises finally.
View Solution
Knowledge Check
- Question 1 - Select One
The block of mass m is at rest. Find the tension in the string A .
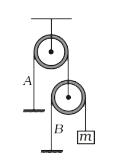 AmgB2 mgC3 mgD4 mg
AmgB2 mgC3 mgD4 mg - Question 2 - Select One
A wooden block of mass 8kg is tied to a string attached to the bottom of a tank. The block is completely inside the water. Relative density of wood is 0.8. Taking g=10m/s2, What is the tension in the string ?
A100NB80NC50ND20N - Question 3 - Select One
A stone of mass 1 kg tied at the end of a string of length 1 m and is whirled in a verticle circle at a constant speed of 3ms−1. The tension in the string will be 19 N when the stone is (g=10ms−1)
Aat the top most point on the vertical circleBat the bottom most point on the vertical circleChalf way downDmaking an angle 30∘ with the vertical
A stone weighing 1 kg is ties to a string of 1m length and whirled over the horizontal top of a rough plane with a speed of 2ms−1. Calculate the tension of the string if the coefficient of friction between the table and the stone is 0.3
View SolutionA wooden block or mass m and density ρ is tied to a string, the other end of the string is fixed to bottom of a tank. The tank is filled with a liquid of density σ with σ>ρ. The tension in the string will be
View SolutionA stone at the end of 1m long string is whirled in a vertical circle at a constant speed of 4ms−1. The tension in the string is 6N when the stone is
View SolutionA stone of mass 5 kg is tied to a string of length 10 m is whirled round in a horizontal circle. What is the maximum speed with which the stone can be whirled around if the string can withstand a maximum tension of 200 N?
View SolutionA bullet of mass 0.01kg and travelling at a speed of 500ms−1 strikes a block of mass 2kg which is suspended by a string of length 5m. The centre of gravity of the block is found to raise a vertical distance of 0.2m. What is the speed of the bullet after it emerges from the block?
View Solution

