A block of mass 2kg is propped from a heught of 40cm on a spring where force constant is 1960Nm−1 The maximum distance thought which the spring compressed by
5 cm
15 cm
20 cm
10 cm
The correct Answer is:D
To solve the problem step by step, we will use the principle of conservation of energy. The potential energy of the block at the height will be converted into the potential energy stored in the spring when it is compressed.
Step 1: Identify the given values
- Mass of the block, m=2kg
- Height from which the block is dropped, h=40cm=0.4m
- Spring constant, k=1960N/m
- Gravitational acceleration, g=9.8m/s2
Step 2: Write the expression for initial potential energy (PE_initial)
The initial potential energy of the block when it is at height h is given by:
PEinitial=mgh
Substituting the values:
PEinitial=2kg×9.8m/s2×0.4m=7.84J
Step 3: Write the expression for final potential energy (PE_final)
When the spring is compressed by a distance xm, the potential energy stored in the spring is given by:
PEfinal=12kx2m
Step 4: Apply the conservation of energy principle
According to the conservation of energy:
PEinitial=PEfinal
Thus,
mgh=12kx2m
Substituting the known values:
7.84=12×1960×x2m
Step 5: Rearranging the equation to find x2m
7.84=980x2m
x2m=7.84980
x2m=0.008
Step 6: Solve for xm
Taking the square root of both sides:
xm=√0.008=0.0894m
Step 7: Convert xm to centimeters
To convert meters to centimeters, multiply by 100:
xm=0.0894×100=8.94cm
Step 8: Conclusion
The maximum distance through which the spring is compressed is approximately 8.94cm.
- Mass of the block, m=2kg
- Height from which the block is dropped, h=40cm=0.4m
- Spring constant, k=1960N/m
- Gravitational acceleration, g=9.8m/s2
The initial potential energy of the block when it is at height h is given by:
PEinitial=mgh
Substituting the values:
PEinitial=2kg×9.8m/s2×0.4m=7.84J
When the spring is compressed by a distance xm, the potential energy stored in the spring is given by:
PEfinal=12kx2m
According to the conservation of energy:
PEinitial=PEfinal
Thus,
mgh=12kx2m
Substituting the known values:
7.84=12×1960×x2m
7.84=980x2m
x2m=7.84980
x2m=0.008
Taking the square root of both sides:
xm=√0.008=0.0894m
To convert meters to centimeters, multiply by 100:
xm=0.0894×100=8.94cm
The maximum distance through which the spring is compressed is approximately 8.94cm.
Topper's Solved these Questions
- WORK , ENERGY AND POWERBOOK - NCERT FINGERTPS ENGLISHCHAPTER - WORK , ENERGY AND POWEREXERCISE - NCERT
18 Videos
- WORK , ENERGY AND POWERBOOK - NCERT FINGERTPS ENGLISHCHAPTER - WORK , ENERGY AND POWEREXERCISE - ASSERTION & REASON
15 Videos
- WAVESBOOK - NCERT FINGERTPS ENGLISHCHAPTER - WAVESEXERCISE - Assertion And Reason
15 Videos
Similar Questions
A block of mass 2 kg is dropped from a height of 40 cm on a spring whose force-constant 1960Nm−1. The maximum distance through which the spring is compressed by
View SolutionA block of 200 g mass is dropped from a height of 2 m on to a spring and compress the spring to a distance of 50 cm. The force constant of the spring is
View SolutionA block whose mass is 2 kg is fastened on a spring whose spring constant is 100 Nm−1 . It is pulled to a distance of 0.1 m from over a frictionless surface and is released at t=0. Calculate the kinetic eneryg of the block when it is 0.05 m away from its mean position.
View SolutionTwo blocks of masses 3 kg and 6kg rest on horizontal smooth surface. The 3 kg block is attached to a spring with a force constant k=900Nm−1 which is compressed 2m from beyond the equilibrium position. The 6 kg mass is at rest at 1m from mean position. 3kg mass strikes the 6 kg mass and the two stick together.

View SolutionA solid cylinder of mass 3kg is rolling on a horizontal surface with velocity 4ms−1. It collides with a horizontal spring of force constant 200Nm−1. The maximum compression produced in the spring will be :
View SolutionA body of mass 2kg collides with a horizontal weight spring of force constant 4Nm−1. The body compresses the spring by 1m from rest position. Find the speed of the block at the instant of collision ? Given that the coefficient of kinetic friction between the body and the surface is 0.1.
View SolutionTwo identical blocks A and B, each of mass m=2kg are connected to the ends of an ideal spring having force constant K=1000Nm−1. System of these blocks and spring is placed on a rough floor. Coefficient of friction between blocks and floor is m=0.5. Block B is passed towards left so that spring gets compressed.
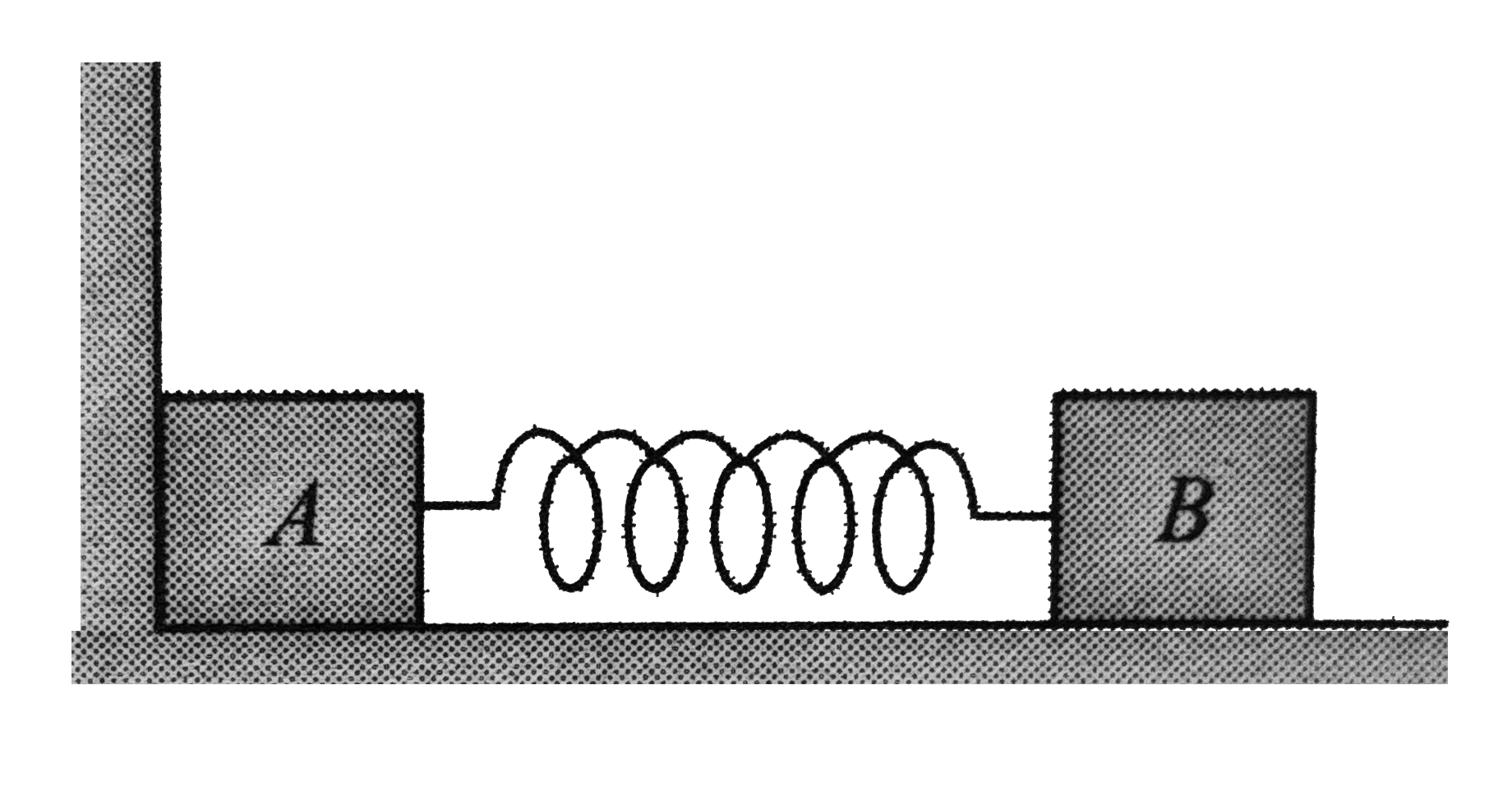
Calculate initial minimum compression x0 of spring such that block A leaves contact with the wall when system is released.
View SolutionA block of mass 2kg is attached with a spring of spring constant 4000Nm−1 and the system is kept on smooth horizontal table. The other end of the spring is attached with a wall. Initially spring is stretched by 5cm from its natural position and the block is at rest. Now suddenly an impulse of 4kg−ms−1 is given to the block towards the wall.
Approximate distance travelled by the block when it comes to rest for a second time (not including the initial one) will be (Take √45=6.70)
View SolutionA block of mass 2kg is attached with a spring of spring constant 4000Nm−1 and the system is kept on smooth horizontal table. The other end of the spring is attached with a wall. Initially spring is stretched by 5cm from its natural position and the block is at rest. Now suddenly an impulse of 4kg−ms−1 is given to the block towards the wall.
Approximate distance travelled by the block when it comes to rest for a second time (not including the initial one) will be (Take √45=6.70)
View SolutionA block of mass 2kg is attached with a spring of spring constant 4000Nm−1 and the system is kept on smooth horizontal table. The other end of the spring is attached with a wall. Initially spring is stretched by 5cm from its natural position and the block is at rest. Now suddenly an impulse of 4kg−ms−1 is given to the block towards the wall.
Find the velocity of the block when spring acquires its natural length
View Solution
