A body of mass 2kg collides with a horizontal weight spring of force constant 4Nm−1. The body compresses the spring by 1m from rest position. Find the speed of the block at the instant of collision ? Given that the coefficient of kinetic friction between the body and the surface is 0.1.
The correct Answer is:1.99ms−1
To find the speed of the block at the instant of collision with the spring, we can use the principle of conservation of energy, taking into account the work done against friction.
1. Identify the Given Values:
- Mass of the body, m=2kg
- Spring constant, k=4N/m
- Compression of the spring, x=1m
- Coefficient of kinetic friction, μ=0.1
- Acceleration due to gravity, g=10m/s2
2. Calculate the Initial Kinetic Energy (KE):
The initial kinetic energy of the block before it collides with the spring is given by:
KE=12mv2
where v is the speed of the block at the instant of collision.
3. Calculate the Potential Energy (PE) Stored in the Spring:
The potential energy stored in the spring when it is compressed by x is given by:
PE=12kx2
Substituting the values:
PE=12×4×(1)2=2J
4. Calculate the Work Done Against Friction (W_f):
The work done against friction can be calculated using:
Wf=friction force×displacement
The friction force is given by:
Ff=μmg=0.1×2×10=2N
Therefore, the work done against friction when the block compresses the spring by x:
Wf=Ff×x=2×1=2J
5. Apply the Energy Conservation Principle:
The initial kinetic energy is converted into the potential energy of the spring and the work done against friction:
KE=PE+Wf
Substituting the known values:
12mv2=2+2
12×2v2=4
Simplifying gives:
v2=4
v=2m/s
Final Answer:
The speed of the block at the instant of collision is 2m/s.
---
- Mass of the body, m=2kg
- Spring constant, k=4N/m
- Compression of the spring, x=1m
- Coefficient of kinetic friction, μ=0.1
- Acceleration due to gravity, g=10m/s2
The initial kinetic energy of the block before it collides with the spring is given by:
KE=12mv2
where v is the speed of the block at the instant of collision.
The potential energy stored in the spring when it is compressed by x is given by:
PE=12kx2
Substituting the values:
PE=12×4×(1)2=2J
The work done against friction can be calculated using:
Wf=friction force×displacement
The friction force is given by:
Ff=μmg=0.1×2×10=2N
Therefore, the work done against friction when the block compresses the spring by x:
Wf=Ff×x=2×1=2J
The initial kinetic energy is converted into the potential energy of the spring and the work done against friction:
KE=PE+Wf
Substituting the known values:
12mv2=2+2
12×2v2=4
Simplifying gives:
v2=4
v=2m/s
The speed of the block at the instant of collision is 2m/s.
Topper's Solved these Questions
Similar Questions
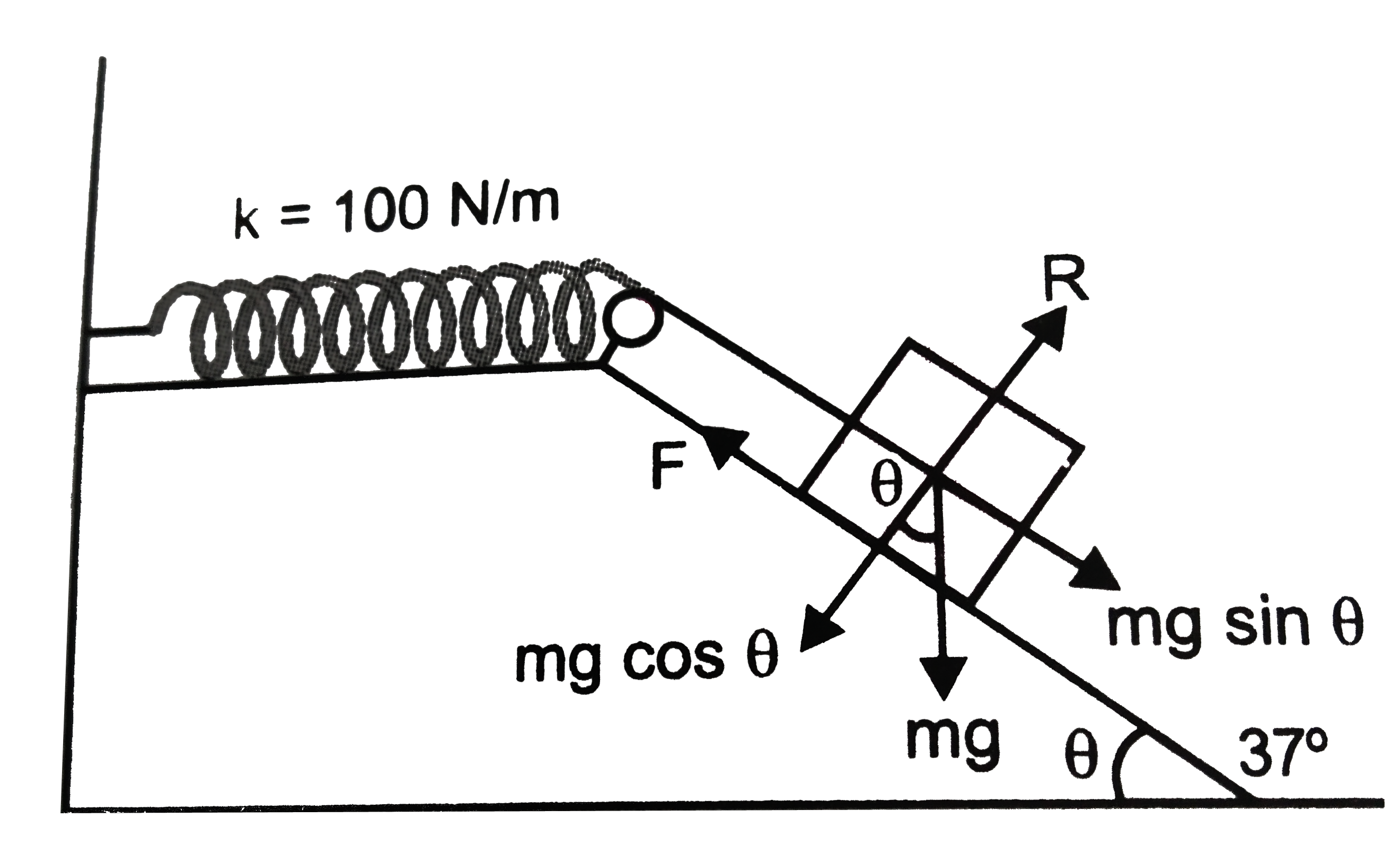
A 1kg block situated on a rough incline is connected to a spring of spring constant 100Nm−1 as shown in figure,. The block is released from rest with the spring in the unstretched position. The block moves 10cm down the incline before coming to rest. Find the coefficient of friction between the block and the incline. Assume that the spring has negligible mass and the pulley is frictionless.
View SolutionA body of mass 0.1 g moving with a velocity of 10 m/s hits a spring (fixed at the other end) of force constant 1000 N/m and comes to rest after compressing the spring. The compression of the spring is
View Solution
Knowledge Check
A 1kg block situated on a rough incline is connected to a spring of spring constant 100Nm−1 as shown in figure,. The block is released from rest with the spring in the unstretched position. The block moves 10cm down the incline before coming to rest. Find the coefficient of friction between the block and the incline. Assume that the spring has negligible mass and the pulley is frictionless.
 A0.2B0.3C0.5D0.6
A0.2B0.3C0.5D0.6A block of mass 2kg is propped from a heught of 40cm on a spring where force constant is 1960Nm−1 The maximum distance thought which the spring compressed by
A5 cmB15 cmC20 cmD10 cm
The block of mass M moving on the frictionless horizontal surface collides with the spring constant k and compresses it by length L . The maximum momention of the block after collision is

View SolutionA block of mass m is slowly pulled along a curved surface from position 1 and 2. If the coefficient of kinetic friction between the block and surface is μ, find the work done by the applied force.

View SolutionA block of mass M=1 kg resting on a smooth horizontal surface is connected to a horizontal light spring of spring constant k=6N/m whose other end is fixed to a verticall wall. Another block of mass m=0.5 kg is placed over the block M. If the coefficient of friction between the two blocks μ=0.4, find the maximum kinetic energy (in J) that the system can have for simple hormonic oscillation under the action of the spring.
View SolutionA body of mass 1.0 kg is suspended from a weightless spring having force constant 600Nm−1. Another body of mass 0.5 kg moving vertically upwards hits the suspended body with a velocity of 3.0ms−1 and gets embedded in it. Find the frequency of oscillations and amplitude of motion.
View SolutionA block of mass m is attached to one end of a mass less spring of spring constant k. the other end of spring is fixed to a wall the block can move on a horizontal rough surface. The coefficient of friction between the block and the surface is μ then the compession of the spring for which maximum extension of the spring becomes half of maximum compression is .
View SolutionTwo rigid bodies A and B of masses 1 kg and 2 kg respectively are rigidly connected to a spring of force constant 400 Nm−1 . The body B rests on a horizontal table. From the rest position , the body A is compressed by 2 cm and then released . Deduce (i) teh frequency of oscillation, (ii) total oscillation energy, (iii) the amplitude of the harmonic vibration of the reaction of the table on body B.

View Solution
