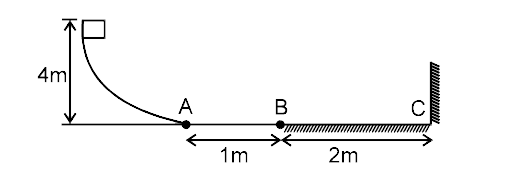
A block of mass m = 0.1 kg is released from a height of 4m on a curved smooth surface. On the horizontal surface, path AB is smooth and path BC offers coefficient of friction μ = 01. If the impact of block with the vertical wall at C be elastic, the total distance covered by the block on the horizontal surface before coming to rest will be (take g=10m/s2)

29 m
49 m
59 m
109 m
The correct Answer is:C
Topper's Solved these Questions
- WORK, POWER AND ENERGYBook:DC PANDEYChapter:WORK, POWER AND ENERGYExercise:B More than One Option is Correct
Explore 26 Videos
- WORK, POWER AND ENERGYBook:DC PANDEYChapter:WORK, POWER AND ENERGYExercise:C Comprehension Type Questions
Explore 18 Videos
- WORK, POWER AND ENERGYBook:DC PANDEYChapter:WORK, POWER AND ENERGYExercise:E Integer Type Questions
Explore 11 Videos
- WORK, ENERGY AND POWERBook:DC PANDEYChapter:WORK, ENERGY AND POWERExercise:MEDICAL ENTRACES GALLERY
Explore 33 Videos
Similar Questions
A block of mass m = 0.1 kg is released from a height of 4 m on a curved smooth surface. On the horizontal surface, path AB is smooth and path BC offers coefficient of friction μ=0.1. If the impact of block with the vertical wall at C be perfectely elastic, the total distance covered by the block on the horizontal surface before coming to rest will be (take g=10ms–2) -
View SolutionA block of mass m is placed at rest on a smooth wedge of mass M placed at rest on a smooth horizontal surface. As the system is released

View Solution
Knowledge Check
A block of mass m = 0.1 kg is released from a height of 4 m on a curved smooth surface. On the horizontal surface, path AB is smooth and path BC offers coefficient of friction μ=0.1. If the impact of block with the vertical wall at C be perfectely elastic, the total distance covered by the block on the horizontal surface before coming to rest will be (take g=10ms–2) -
 A29 mB49 mC59 mD109 m
A29 mB49 mC59 mD109 mA block of mass m = 0.1 kg is released from a height of 4 m on a curved smooth surface. On the horizontal surface, path AB is smooth and path BC offers coefficient of friction = 0.1. If the impact of block with the vertical wall at C be perfectely elastic, the total distance covered by the block on the horizontal surface before coming to rest will be (take g = 10 ms–2) -
 A29mB49mC59mD109m
A29mB49mC59mD109mFigure shows an irregular wedge of mass m placed on a smooth horizontal surface. Part BC is rough.
If the coefficient of friction between the block and wedge is μ, and the block comes to rest with respect to wedge at a point E on the rough surface then BE will beAHμBH−hμChμDnone of these
A block of mass m is placed at rest on a smooth wedge of mass M placed at rest on a smooth horizontal surface. As the system is released

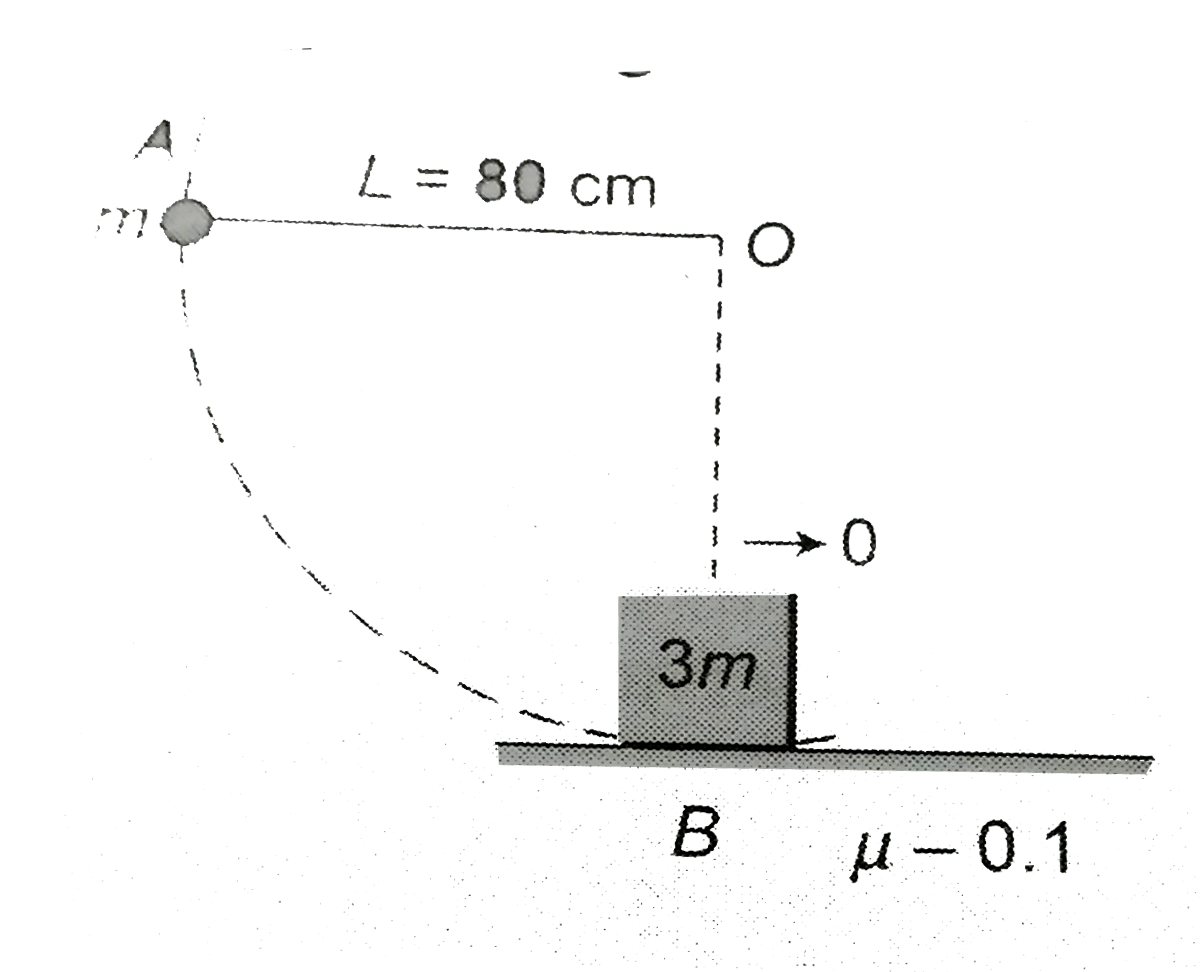
View SolutionThe ball A of mass m is released when the string is horizontal. It strikes a block B of mass 3m kept on a rough surface of friction coefficient μ=0.1. If a head on elastic collision takes place , find the maximum distance travelled by the block on a rough surface.
View SolutionA block of mass 4 kg is released from the top of an inclined smooth surface as shown in figure If spring constant of spring is 100M/m and block comes to rest after compressiong spring by 1 m, find the distance travelled by the block before it comes t o rest.

View SolutionA block of mass 4 kg is released from the top of an inclined smooth surface as shown in figure If spring constant of spring is 100N/m and block comes to rest after compressing spring by 1 m, find the distance travelled by the block before it comes t o rest.

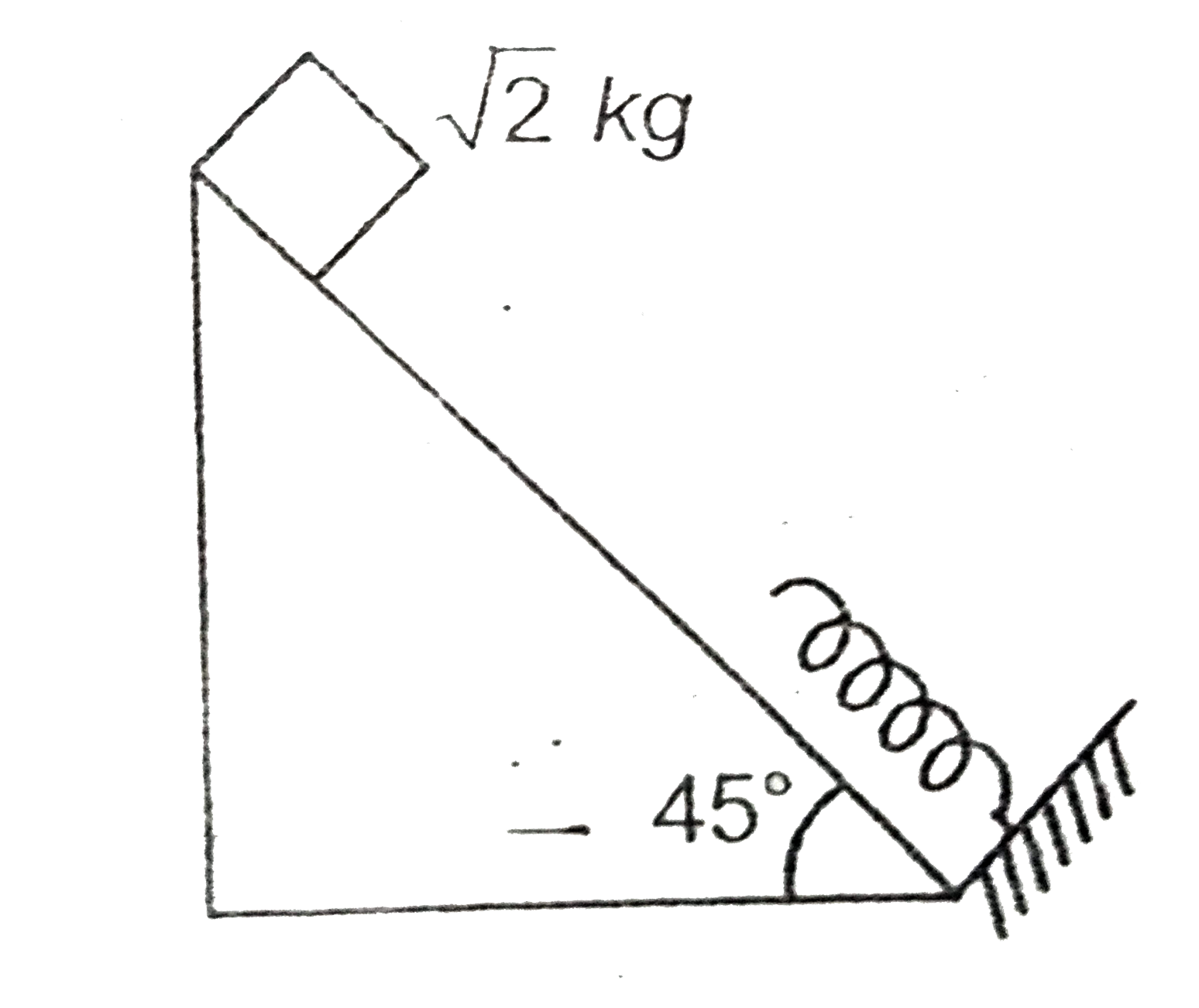
View SolutionA block of mass √2 kg is released from the top of an inclined smooth surface as shown in fighre. If spring constant of spring is 100 N/m and block comes to rest after compressing the spring by 1 m, then the distance travelled by block befor it comes to rest is
View Solution
