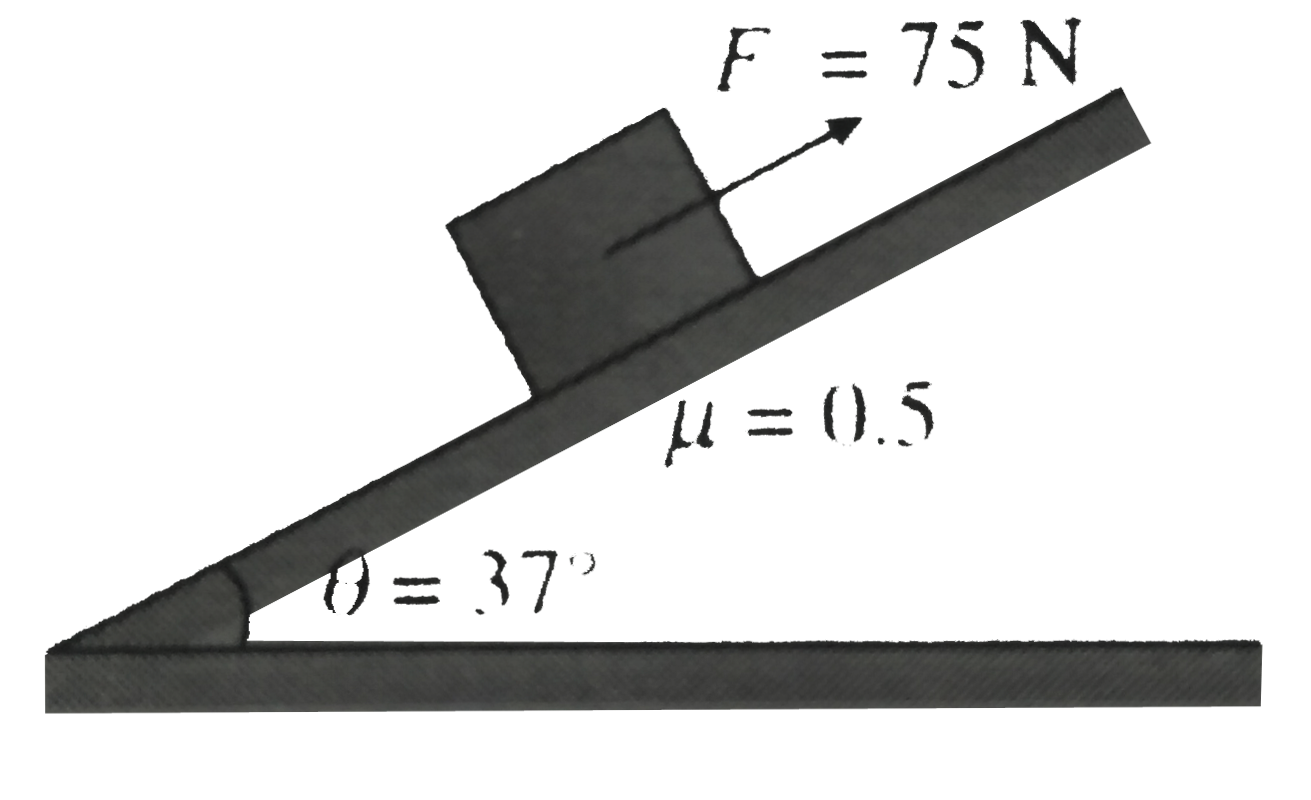
A block of mass $M = 10 k g$ is placed inclined plane , inclined at angle $θ = 37^{\circ}$ with horizontal The coefficient of friction between the block and inclined is $μ = 0.5$
a. Calculate the acceleration of the block when it is released
b. Now a force $F = 75 N$ is appling on block as shown find out the acceleration of the block If the block is initially at rest .
c. In case (b), how much force should be added to $75 N$ force so that block the starts to move up the incline.
d. In case (b), what is the minimum force by which $75 N$ force should be replaced with so that the block does not move?

Video Solution

Text Solution

Verified by Experts

a. Here angle of repose $a = \tan^{- 1} (μ_{s})$
$α = {Tan}^{- 1} (\frac{1}{2}) = 30^{\circ}$

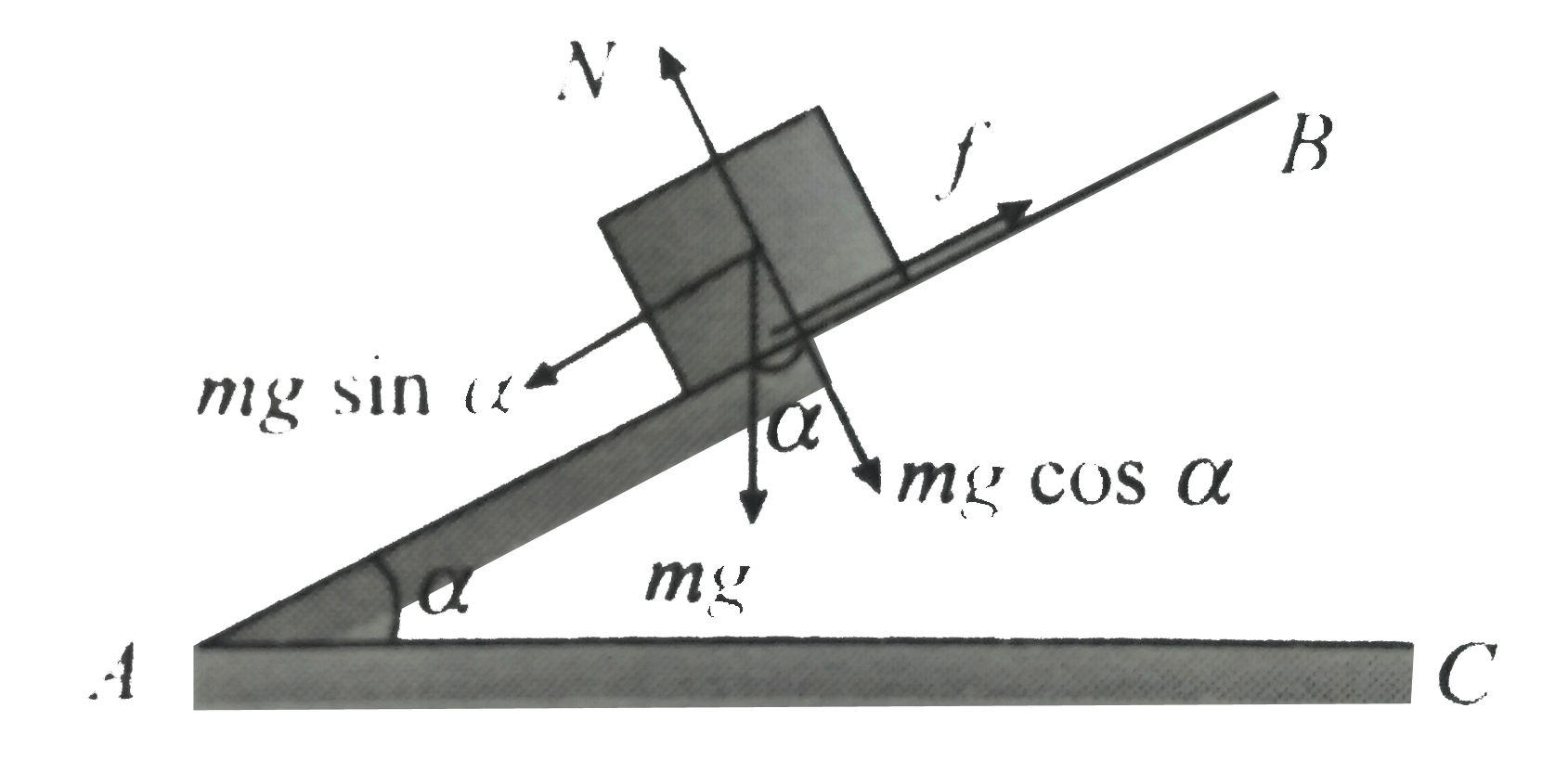
The angle of inclination is greater than the angle of repose
For the acceleration of block .
$M g \sin θ - μ N = M a$
$\Rightarrow a = g \sin θ - μ g \cos θ$
$= 10 ({\sin 37}^{\circ} - 0.5 {\cos 37}^{\circ})$
b. If external force $F = 75 N$ is applied on the block

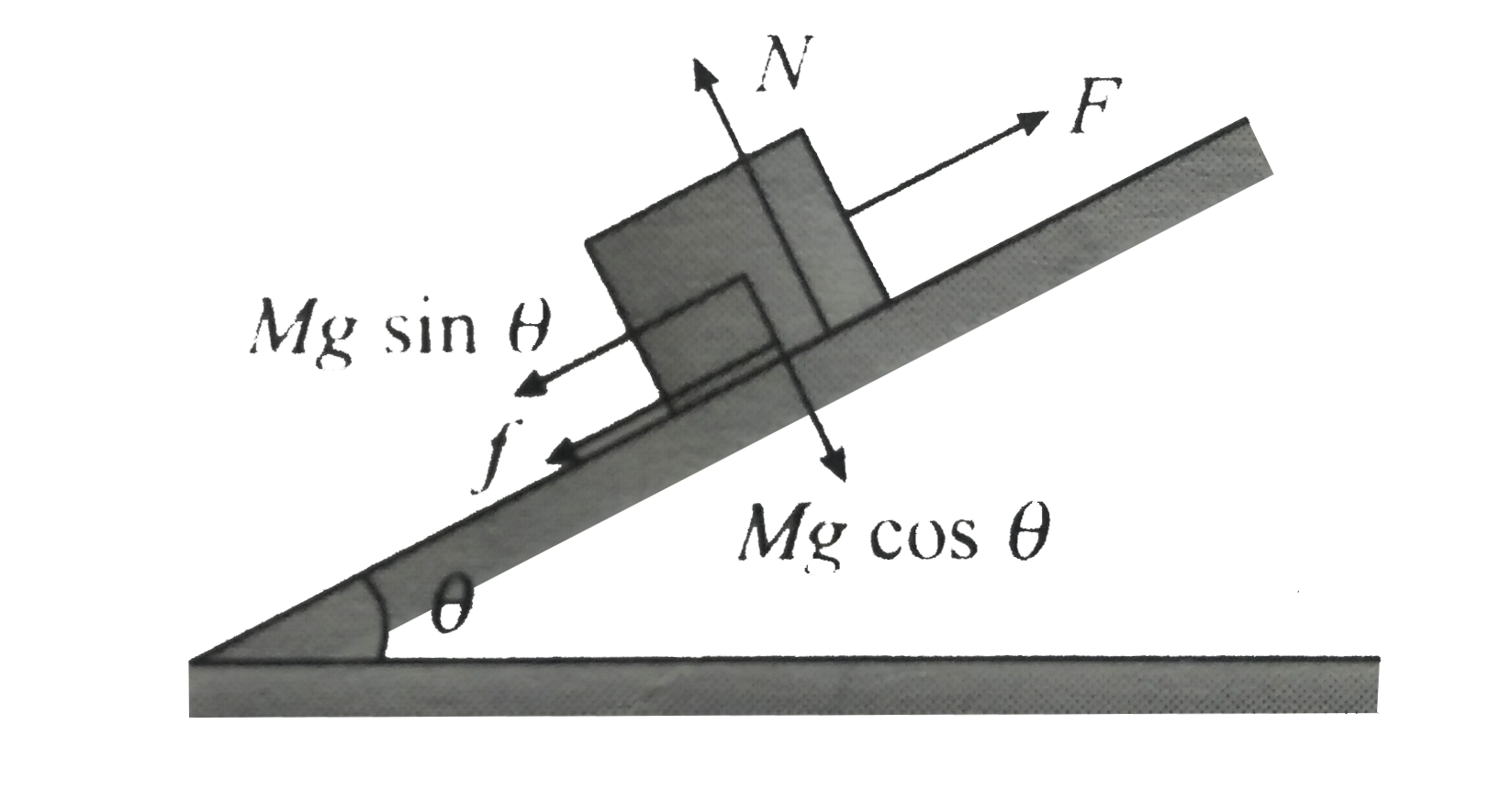
Let as find net driving force acting on block . parallel to incliend two externalforces are acting are one in upward direction $F$ and other is the component of weight in the direction downward the plate $M g \sin θ$
Net driving force $f_{driving} = F - M g \sin θ$
$\Rightarrow F_{driving} = 75 - 10 \times 10 \times {\sin 37}^{\circ} = 75 - 60 = 15 N$
Maximum resisting force that opposw relative motion maximum friction force (or $f_{lim})$
$f_{lim} = μ_{s} M g \cos θ$
$= 0.5 \times 10 \times 10 \times {\cos 37}^{\circ} = 40 N$
Here $F_{driving} < F_{resisting}$ Hence, the block will not move and friction will be static and will act is the direction opposite to driving force i,e in downward direction .
c. To move the block the least value of driving force should be $40 H N$ . But in above case, driving force is $15 N$ (up)Hence if we add $δ F = 25 N$ in upward direction , the block will overcome maximum resistance force (or friction) as starts moving up
$∴ 60 + 40 = 75 + δ F \Rightarrow δ F = 25 N$
d. As resisting force which is maximum friction is $40 N$ and the component of weight parallel to incline is $60 N$ and acting downward If the only component of the weight in direction downward the incline plane

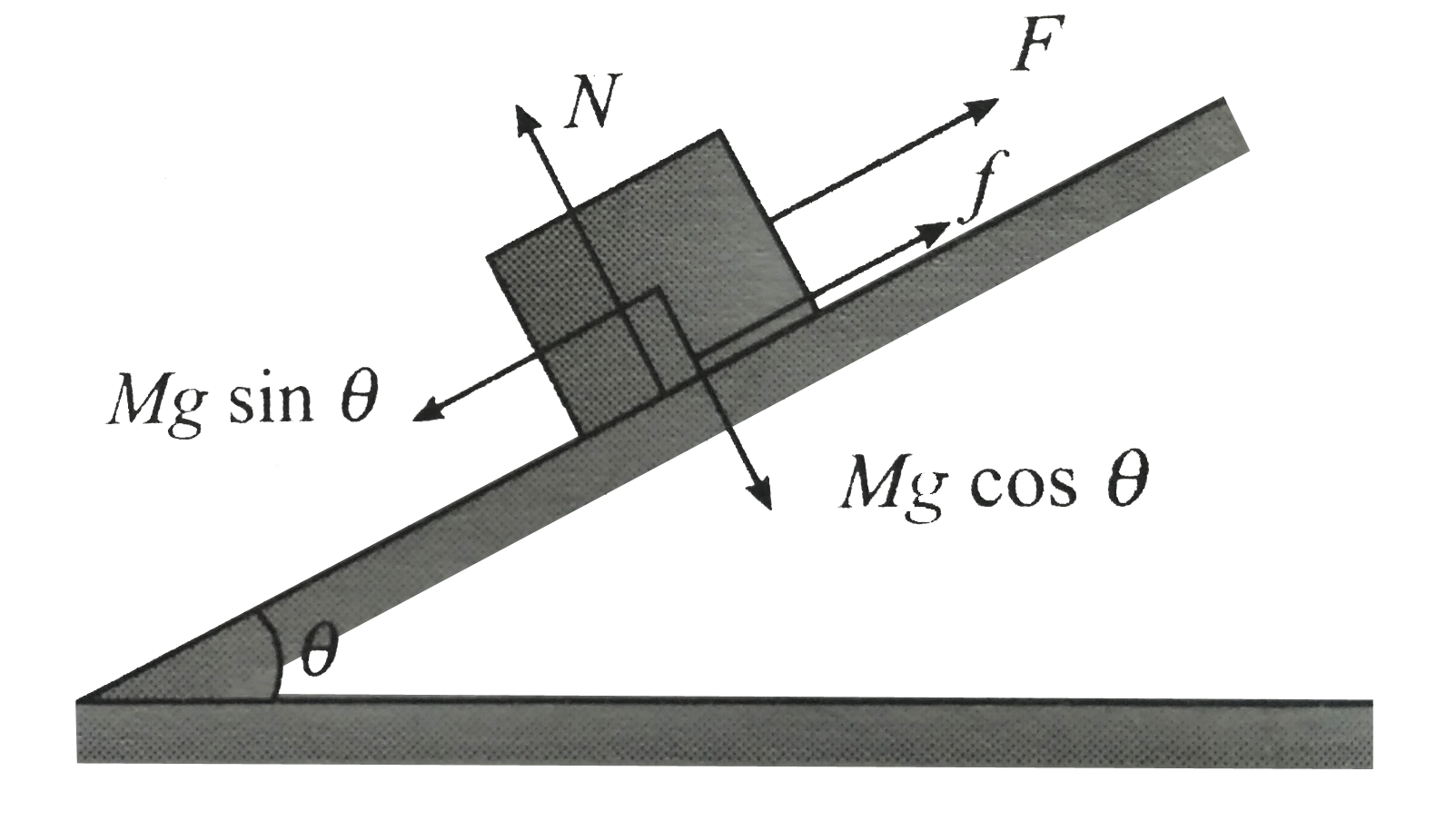
In this case , friction will act in upward direction hence the required value of $F$ to make in equalibrium
$F + 40 = 60$
or $F = 20 N$

A block of mass m slides down an inclined plane which makes an angle $θ$ with the horizontal. The coefficient of friction between the block and the plane is $μ$ . The force exerted by the block on the plane is
A $m g cos θ$
B $\sqrt{μ^{2} + 1} m g cos θ$
C $\frac{μ m g cos θ}{\sqrt{μ^{2} + 1}}$
D $μ m g θ$
A block of mass m is placed on a rough plane inclined at an angle $θ$ with the horizontal. The coefficient of friction between the block and inclined plane is $μ$ . If $θ < {tan}^{- 1} (μ)$ , then net contact force exerted by the plane on the block is :
Amg cos $θ$
Bmg
Cmg sin $θ$
DNone of these
A block is lying on an inclined plane which makes $60^{\circ}$ with the horizontal. If coefficient of friction between block and plane is 0.25 and $g = 10 m / s^{2}$ , , then acceleration of the block when it moves along the plane will be
A $2.50 m / s^{2}$
B $5.00 m / s^{2}$
C $7.4 m / s^{2}$
D $8.66 m / s^{2}$