A block of mass m attached to a massless spring is performing oscillatory motion of amplitude A on a frictionless horizontal plane. If half of the mass of the block off when it is passing through its mean position, the amplitude of oscillation for the remaining system become fA. The value of f is .
√2
1√2
12
1
To solve the problem step by step, we will analyze the situation using the principles of conservation of momentum and the properties of oscillatory motion.
Step 1: Understand the Initial Conditions
The block of mass m is attached to a massless spring and is performing oscillatory motion with an amplitude A. At the mean position, the velocity of the block is maximum, given by:
v=Aω
where ω is the angular frequency of the oscillation.
Step 2: Apply Conservation of Momentum
When half of the mass of the block is removed as it passes through the mean position, we need to apply the conservation of momentum.
Let:
- Initial mass m1=m
- Initial velocity u=Aω
- Final mass m2=m2
- Final velocity v1
Using conservation of momentum:
m1u=m2v1
Substituting the known values:
m(Aω)=m2v1
Step 3: Solve for Final Velocity
From the equation:
mAω=m2v1
We can cancel m from both sides (assuming m≠0):
Aω=12v1
Thus, we can express v1:
v1=2Aω
Step 4: Relate Angular Frequency to Amplitude
The angular frequency ω is given by:
ω=√km
When the mass is halved, the new angular frequency ω′ for the remaining mass m2=m2 is:
ω′=√km/2=√2km=√2ω
Step 5: Find the New Amplitude
The new amplitude A′ can be related to the initial amplitude A and the new velocity v1:
Using the relationship of maximum velocity:
v1=A′ω′
Substituting for ω′:
2Aω=A′√2ω
Cancelling ω from both sides (assuming ω≠0):
2A=A′√2
Solving for A′:
A′=2A√2=A√2
Step 6: Determine the Value of f
Given that the new amplitude A′=fA, we can equate:
fA=A√2
Thus, we find:
f=√2
Final Answer
The value of f is:
√2
The block of mass m is attached to a massless spring and is performing oscillatory motion with an amplitude A. At the mean position, the velocity of the block is maximum, given by:
v=Aω
where ω is the angular frequency of the oscillation.
When half of the mass of the block is removed as it passes through the mean position, we need to apply the conservation of momentum.
- Initial mass m1=m
- Initial velocity u=Aω
- Final mass m2=m2
- Final velocity v1
m1u=m2v1
Substituting the known values:
m(Aω)=m2v1
From the equation:
mAω=m2v1
We can cancel m from both sides (assuming m≠0):
Aω=12v1
Thus, we can express v1:
v1=2Aω
The angular frequency ω is given by:
ω=√km
When the mass is halved, the new angular frequency ω′ for the remaining mass m2=m2 is:
ω′=√km/2=√2km=√2ω
The new amplitude A′ can be related to the initial amplitude A and the new velocity v1:
Using the relationship of maximum velocity:
v1=A′ω′
Substituting for ω′:
2Aω=A′√2ω
Cancelling ω from both sides (assuming ω≠0):
2A=A′√2
Solving for A′:
A′=2A√2=A√2
Given that the new amplitude A′=fA, we can equate:
fA=A√2
Thus, we find:
f=√2
The value of f is:
√2
Topper's Solved these Questions
Similar Questions
A block of mass 4kg attached with spring of spring constant 100N/m is executing SHM of amplitude 0.1m on smooth horizontal surface as shown in figure. If another block of mass 5kg is gently placed on it, at the instant it passes through the mean position and new amplitude of motion is n−1 meter then find n. Assuming that two blocks always mvoe together .
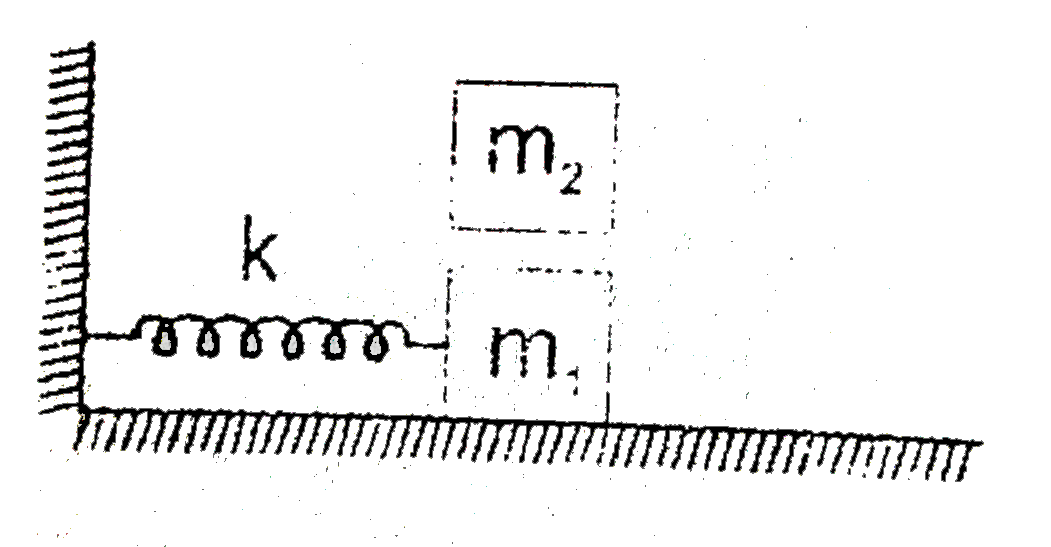
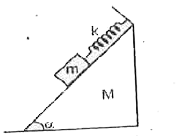
View SolutionA system consisting of a smooth movable wedge of angle α and a block A of mass m are connected together with a massless spring of spring constant k, as shown in the figure. The system is kept on a frictionless horizontal plane. If the block is displaced slighlly from equilibrium and left to oscillate, find the frequency of small oscillations.
View Solution
Knowledge Check

A block of mass m is attached to two unstretched springs of spring constant k, each as shown. The block is displaced towards right through a distance x and is released The speed of the block as it passes through the mean position will beAx√m2kBx√2kmCxmkDx2kmA mass m, connected to a horizontal spring performs SHM with amplitude A. While mass m, is passing through mean position, another mass m, is placed on it so that both the masses move together with amplitude A,. The ratio of
A[m1m1+m2]12B[m1+m2m1]12C[m2m1+m2]12D[m1+m2m2]12A block of mass M placed on a frictionless horizontal table is pulled by another block of mass m hanging vertically by a massless string passing over a frictionless pulley. The tension in the string is :
AmM+mgBMM+mgCM+mmngDMnM+ng
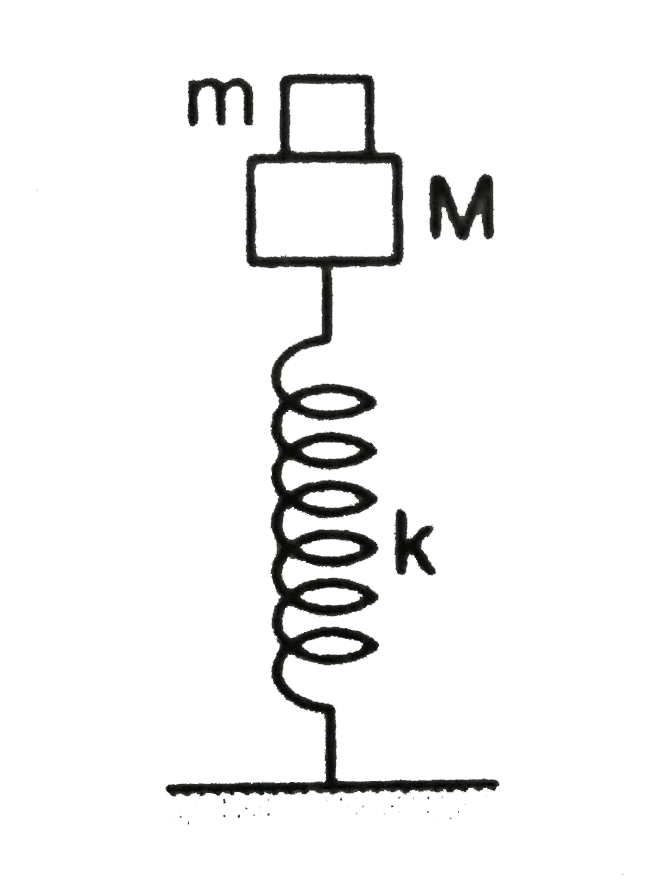
A small block of mass m is kept on a bigger block of mass M which is attached to a vertical spring of spring constant k as shown in the figure. The system oscilates verticaly. a.Find the resultant force on the smaller block when it is displaced through a distance x above its equilibrium position. b. find the normal force on the smaller blok at this position. When is this force smallest smaller block at this position. When is this force smallest in magnitude? c. What can be the maximum amplitude with which the two blocks may oscillate together?
View SolutionA block of mass 1 kg attached to a spring is made to oscillate with an initial amplitude of 12 cm. After 2 minutes the amplitude decreases to 6 cm. Determine the value of the damping constant for this motion. (take In 2 =0.693 )
View SolutionA block of mass m is connected to another block of mass M by a massless spring of spring constant K. Blocks are kept on a smooth horizontal plane. Initally both the blocks the at rest and spring is unstressed. Force F is applied on M to right as shownin the figure then which of the following is correct ?

View SolutionA block of mass m is connected to a massless pulley and mass-less spring of stiffness k. The pulley is frictionless. The string is mass-less. Initially the spring is unstretched when the block is released. When the spring is maximum stretched, find the ratio of tenstion in the rope and weight of the block.

View SolutionA horizontal spring-block system of mass 1kg executes SHM of amplitude 10 cm. When the block is passing through its equilibrium position another mass of 1kg is put on it and the two move together.
View Solution
